重庆市中医药类专业卫生技术人员需求预测模型研究＊

吴海峰，何 坪△，邓 宇，潘 伦，周天寒，何丽芳，方明金

（1.重庆医药高等专科学校 401331；2.重庆市卫生局 401147）

中医药学是中华民族、中国文化的宝贵遗产，是流传数千年至今仍在发挥作用的学科。重庆是传统的中医药强市，人民群众对中医药有广泛的需求。重庆直辖以来，全市经济社会事业突飞猛进，但中医药事业发展缓慢，中医药人才数量紧缺且质量较低，难以适应本市经济社会的快速发展。针对本市中医药卫生人才数量紧缺的现状[1－4]，需对其需求进行预测研究。而数据预测领域，预测方法多种多样，本文采用常用的几种预测方法，对中医类卫生人员需求进行预测，以此为中医类卫生人员需求预测提供方法学参考。

1 资料与方法

1.1 一般资料 资料来源于2001～2010年重庆市统计年鉴、重庆市卫生统计年鉴。

1.2 方法 建立3个预测模型，预测本市中医药专业技术人才需求，采用相关统计量指标对各模型的预测效果进行评价以寻求最佳预测模型。另外，在建立各预测模型时，还需将研究数据分为2个部分，即内样本（训练样本）数据用于建立模型，而外样本（预测样本）数据用于验证已建立的预测模型的预测效果。取2001～2008年本市卫生人员数据为研究内样本，而2009～2010年本市卫生人员数据为研究外样本。

1.2.1 多元线性回归预测模型（模型Ⅰ）的建立 多元线性回归模型分析预测法[5－7]，通过对2个或2个以上的自变量（影响因素）与1个因变量（预测变量）的相关分析，建立预测模型进行预测的方法。当自变量与因变量之间存在线性关系时，称为多元线性回归模型分析。在建模过程中，由于初选的影响因素众多（通过查阅统计年鉴，本文初选16个因素），需对其进行筛选，筛选方法为“向前选择法”，即根据各自变量对因变量的影响显著性，若符合入选标准（入选标准为0.4），则依次进入模型方程。

1.2.2 主成分回归预测模型（模型Ⅱ）的建立 主成分回归模型分析法[8－10]，先对各自变量进行主成分分析，避开自变量之间的相关性，进而分析各自变量对因变量的影响。即它先将原来的指标通过主成分分析重新组合成一组新的相互独立的综合指标来代替原来的指标，同时根据实际需要从中提取较少的几个综合指标来尽可能多地反映原指标的信息；之后将这些综合指标看作自变量建立回归方程，实现预测。该方法避开了多元回归分析中自变量间的多重共线性。本研究选取2个主成分，此时方差累积贡献率为94.82%，通过2个主成分的线性表达式计算主成分得分，之后将2个主成分看做自变量参与多元回归模型分析。在2个主成分的多元回归分析中，仍选择“向前法”筛选变量，入选标准为0.4。

1.2.3 前馈型（back prpagation，BP）人工神经网络（artificial neural networks，ANN）预测模型（模型Ⅲ）的建立 ANN近年来在预测领域中一直是研究的热点，建立模型Ⅲ时，首先应考虑网络结构，由于具有一个单隐含层的3层前馈型神经网络能以任意精度逼近任一研究数据，因此，选择3层前馈型神经网络结构，即1个输入层，1个隐含层，1个输出层；其次应考虑网络各层节点数、激励函数及训练函数。本文通过实验法验证，即先根据经验确定范围，然后在此范围内选择不同的节点数目，选择不同的激励函数和训练函数，以最终预测误差为评选标准，选择最佳节点数、激励函数及训练函数，最终所选的BP神经网络结构如表1所示。

1.2.4 效果评价 采用均方根误差（root mean square error，RMSE）以及平均绝对百分 比误差（mean absolute percentage error，MAPE）2个指标来考察各模型对研究数据泛化能力。RMSE和MAPE的值越小，说明预测值与实测值之间的差别越小，预测效果就越好。

1.3 统计学处理 采用SAS8.2统计分析软件及MATLAB数据处理软件。

2 结 果

模型Ⅲ对重庆市中医药类专业卫生技术人员需求的预测效果比模型Ⅰ、Ⅱ好，见图1和表2。模型Ⅲ对本市2011～2013年中医药类卫生专业技术人员总数预测结果见表3。

表1 模型Ⅲ网络最终结构

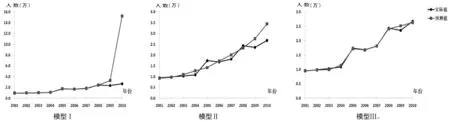
图1 3个模型预测2009、2010年中医药类卫生专业技术人员总数预测值与实际值对比图

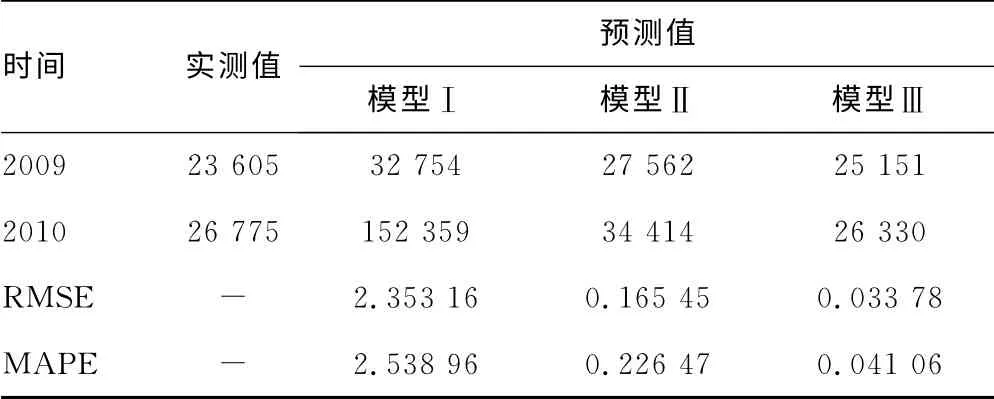
表2 3个模型预测2009～2010年中医药类卫生专业技术人员总数预测值与实际值比较

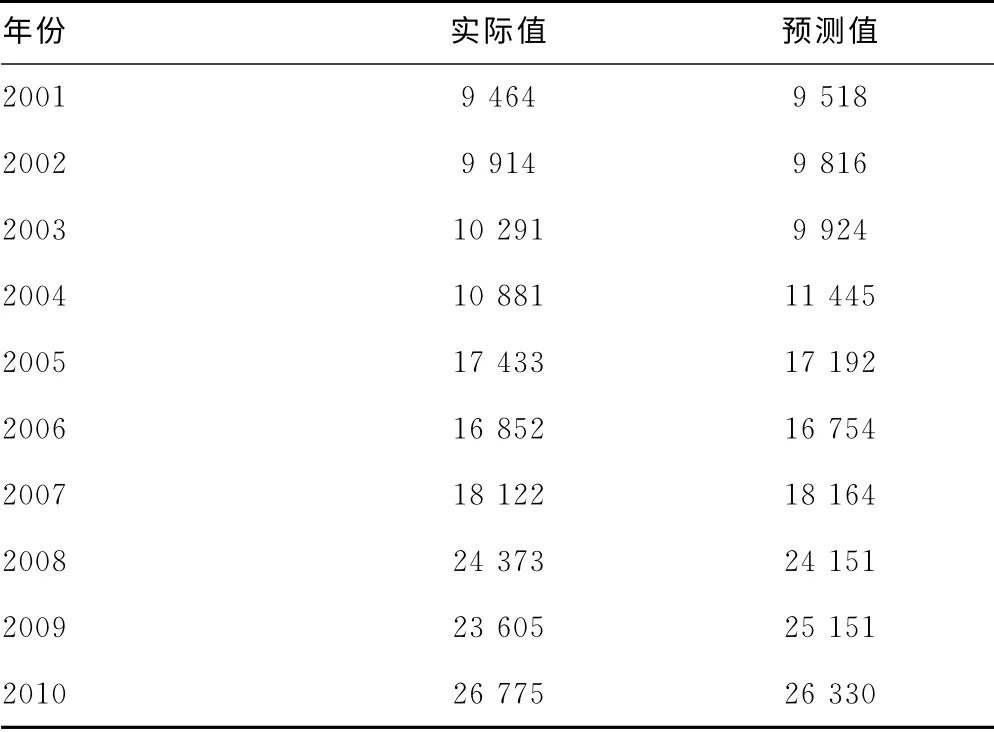
表3 模型Ⅲ对本市2001～2010年中医药类卫生专业技术人员总数预测结果

3 讨 论

为了探讨寻求最佳模型预测重庆市中医药类卫生技术人员总数，分别建立了3个预测模型，即多元线性回归预测模型、主成分回归预测模型、BPANN预测模型，各模型的优缺点：（1）当研究各影响因素与因变量之间的关系，并通过这些影响因素预测因变量时，多元线性回归模型是较常采用的研究方法。但多元线性回归需要因变量数据呈正态性分布、各影响因素之间相互独立且与因变量之间呈线性变化趋势，众多限制条件不仅限制了多元线性回归的应用，更影响其预测效果。（2）主成分回归模型先将原来的影响因素指标通过主成分分析重新组合成一组新的相互独立的综合指标来代替原来的指标，同时根据实际需要从中提取较少的几个综合指标来尽可能多地反映原指标的信息；之后将这些综合指标看作自变量进行多元线性回归，从而建立回归方程，实现预测，可见该方法既避开了多元回归分析中自变量间的多重共线性问题，也能在尽量保留原始数据信息前提下，达到减少自变量个数的目的，因而与多元线性回归相比，具有一定优势。但主成分回归同样也要求各主成分指标与因变量之间线性相关要求，且通过综合原始数据信息而得到的主成分，反而使得其与因变量线性相关性判断更加困难。（3）不管是多元线性回归模型，还是主成分回归模型，在建模预测时，都要求因变量满足正态性和自变量相互独立性，且要求自变量与因变量须呈线性相关关系，而ANN无此限制[11－13]。并且加入隐含层的ANN可以逼近从输入到输出间的任意非线性映射，避开类复杂的参数估计过程，直接给出结果，简单直观，易于操作，因而更具有优势。但ANN是基于自动学习理论而提出的灰色学习系统，它直接给出结果，不能通过具体模型方程确切表达出输入与输出之间的映射关系，这与回归预测模型有所区别；并且ANN存在不稳定性现象[14]，即对同一训练数据重复运行模型程序后得到的结果并不总是一样，不稳定性现象主要是由于初始网络参数为随机数，而不同的初始网络参数又会导致网络不同的输出造成的。此外，人工神经网络理论尚不十分成熟，如隐含层节点数的选择目前尚无统一认可的选择依据或公式，本研究所建立的人工神经网络在选择隐含层节点时，先给出最佳隐含层节点所在大致区间，然后分别取该区间的任一整数为隐含层神经元的个数，分别建立神经网络模型，通过同一研究数据的计算与分析，以最终的网络训练误差为选择标准，以决定最优隐含层节点数目。

[1]王淑军.从“十二五”规划看中医药新布局[J].中国中医药导报，2011（3）：65－66.

[2]武继彪，徐传庚，宋永刚，等.中医相关类职业教育现状分析与人才需求预测[J].中医教育，2010，29（1）：80－83.

[3]裘索.中医药人才培养现状及对策探讨[J].中医药学刊，2005，23（3）：146－148.

[4]张学清，席晶晶，崔颖.西部四省村卫生室基本卫生服务能力现况调查[J].中华医院管理杂志，2009，25（5）：353－355.

[5]杨月，沈进.多元线性回归模型分析在人才需求预测中的应用[J].商场现代化，2006（32）：40－41.

[6]袁海平，赵科，王继伦.多元线性回归地应力场反演方法研究[J].有色金属科学与工程，2011，2（1）：61－64.

[7]剧瑁.基于多元线性回归模型与应用软件对世博会影响力评估研究[J].自动化与仪器仪表，2011（2）：106－107.

[8]龙德江.基于主成分回归模型分析的城市需水量预测[J].水科学与工程技，2010（1）：17－19.

[9]姜信君，佟瑞洲.大气污染主成分回归预报模型及试报分析[J].辽宁大学学报：自然科学版，2010，37（2）：92－94.

[10]尹元福.影响吉林省农村地区生活水准因素的主成分回归模型分析[J].中国农学通报，2011，27（4）：418－423.

[11]林和平，朱道敏，刘庆超.二次回归模型分析人工神经网络[J].信息技术，2011（9）：38－41.

[12]裴志.BP人工神经网络隐层结构设计的思考[J].科技研究，2011（10）：44－45.

[13]周利锋，高尔生.人工神经网络的应用[J].现代预防医学，1998，25（3）：272－274.

[14]Chiang JH.A hybrid neural network in handwriting word recognition[J].Neural Networks，1998，11（3）：337－346.