水面舰船附近气泡运动数值模拟

王诗平 张阿漫 程潇欧 姚熊亮 陈海龙

哈尔滨工程大学船舶工程学院，黑龙江哈尔滨 150001

0 引言

当在自由面与水中结构物附近产生气泡时，需要同时计入两者对气泡脉动的影响［1-2］。水下爆炸被广泛应用于国防和工业等领域，其生成气泡的运动特性由于浮力和边界的特性而非常复杂。当气泡在刚性壁面附近运动时，刚性壁面会对气泡产生吸引而诱导其产生朝向刚性壁面方向的射流；当气泡在自由面附近运动时，自由面会对气泡产生排斥而使射流方向远离自由面，浮力的存在会使气泡的运动形式更加复杂［3］。在数值模拟中描述在壁面、自由面和浮力共同作用下气泡运动特性的研究较少，为此，本文将以计入自由面效应的格林函数替代基本格林函数，采用边界元法研究水面舰船附近气泡的运动特性，同时计入浮力的影响。

在对自由面进行建模时，需要将自由面区域设置得较大，或者将自由面建成封闭的四面体，这就导致自由面网格划分较多［4］，严重影响计算速度。因此，本文将采用修正格林函数，在不对自由面进行建模的情况下考虑自由面对气泡脉动的影响。

在考虑水下爆炸气泡与水面舰船的相互作用时，由于药包在水下爆炸生成的气泡与自由面较近，因此需要考虑自由面对气泡运动的影响，此时，在建立气泡运动模型时，需要同时考虑气泡表面、自由面和舰船水线面以下的部分。如此，就会产生一系列的问题：首先，自由面需要大量的三维网格，这样会增加数值计算量；其次是自由面与结构的交界，这不仅会导致数值的不稳定，而且在处理结构与自由面的交界处时会带来复杂的数值步骤。因此，本文将采用一种新的方法计算自由面与水面舰船附近气泡的运动，通过在气泡和水面舰船镜像位置分布点汇，使得在计算过程中避免了对自由面建模的必要，从而提高计算速率。

1 数值模型及有效性验证

假定水下爆炸气泡周围的流场为无粘、无旋且不可压缩的理想流体，满足拉普拉斯方程［5-7］：

下面，建立此镜像法的数学模型。按照此方法，只需建立水面舰船的水下部分，舰船水面以上的部分则可忽略。图1所示为水面舰船（水下部分）、爆炸气泡及其镜像，其中水面舰船的船长为L，船宽为B，吃水为H。在数值计算中，将水面舰船及其镜像划分为3个区域：水面舰船自由面以下部分（S＋）、水线面结点（I）以及水面舰船自由面以下部分的镜像（S-）。气泡表面及气泡表面的镜像分别表示为B＋和B-。在此种情况下，可将拉普拉斯方程表示成如下边界积分方程：

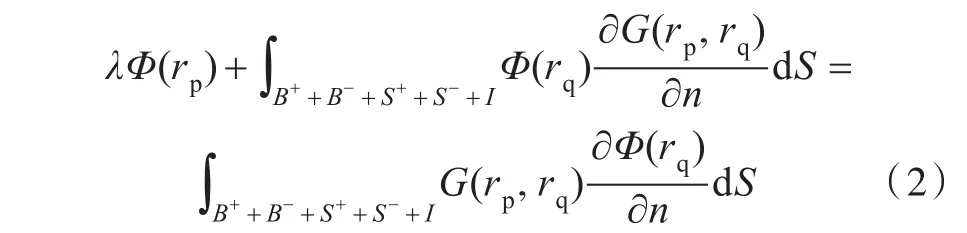
式中，rp为固定点；rq为积分点；λ为流场中的立体角。方程（2）联系速度势Φ和法向速度

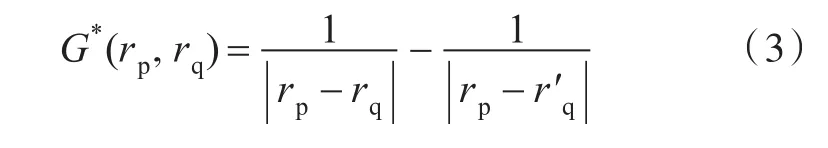
式中，r′q表示rq关于水平面z=0的镜像点。则此时边界积分方程可表示为：

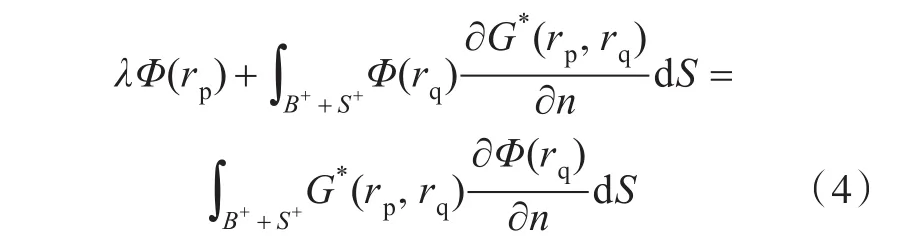
从方程（4）中可以看出，采用考虑自由面效应的格林函数取代基本格林函数后，边界积分方程得到了简化，仅需在船体水线以下部分和气泡表面分布源和偶极即可得到计入自由面效应的边界积分方程。

气泡脉动过程满足如下伯努利方程：

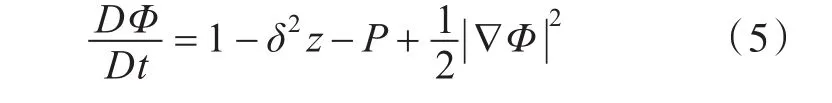
式中，δ为无量纲浮力参数，伯努利方程的无量纲化参考。本文将均采用无量纲变量，上述方程的无量纲化过程参考文献［9］。

图1 舰船模型和水下部分及其镜像Fig.1 Ship model’s underwater part and its image

采用此格林函数可以计及自由面对气泡动态特性的影响，下面将检验该方法在不建立自由面网格的基础上考虑自由面效应的有效性。采用本文的格林函数运用三维模型进行计算，并将计算结果与自由面附近轴对称气泡运动特性的数值结果进行了比较。本文选取初始无量纲距离d＝1.4，强度参数 ε＝200，浮力参数 δ＝0，比热比 γ＝1.25，对应气泡初始半径 R0＝0.116。将气泡表面划分成642个结点，1 280个单元。两种结果的对比如图2所示。图2（a）～图2（c）是采用考虑了自由面效应的三维气泡脉动结果，在计算过程中没有对自由面进行建模，图中，z＝0的位置即为自由面的位置。图 2（e）～图 2（f）是在相同参数下采用轴对称程序的计算结果。对于三维数值模拟，气泡初始为球形，然后迅速膨胀，在t＝0.75时刻膨胀至最大体积（图2（a）），随后，气泡开始坍塌，并在 t＝1.53时刻形成向下的射流（图2（b）），在t＝1.64时刻，形成扁平的宽射流（图2（c））。在整个计算过程中，气泡的整体位置是向下移动的，其计算结果与图2（d）～图2（f）中列出的轴对称结果相似。由图中可看到，采用考虑了自由面效应的格林函数的结果与采用基本格林函数的二维轴对称气泡的结果基本相同，气泡都在自由面的Bjerknes力作用下产生了远离自由面的射流。在基于不同方法的气泡脉动过程中，无量纲体积随无量纲时间的变化曲线如图3所示。由图3可看出，采用考虑了自由面效应的格林函数计算的体积与轴对称模型吻合较好，验证了本文数值方法的有效性。

在处理水面舰船问题时，水面舰船被自由面分割成水上部分和水下部分，忽略水上部分后，边界不再封闭，因此，在计算奇异积分时，Hii=4π-Hij的性质不再成立。边界上立体角的求解可以通过如下2种方法求解。

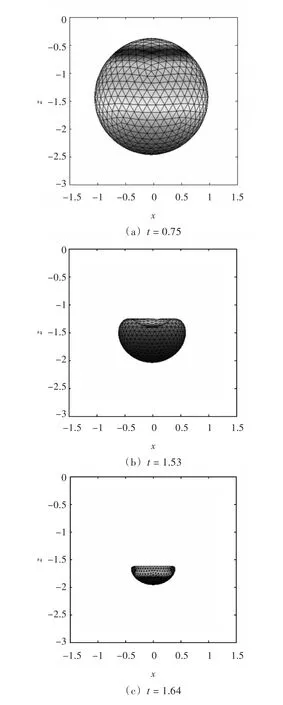
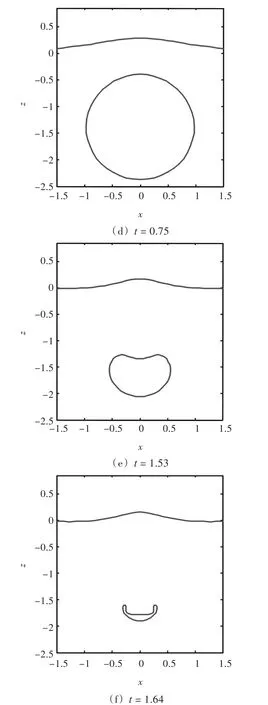
图2 自由面附近单个气泡三维结果与轴对称结果对比Fig.2 Comparison of three dimensional and axisymmetrical single bubble near free surface

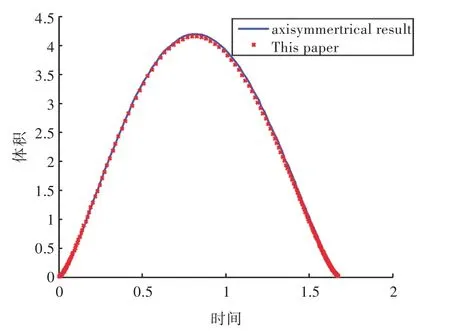
图3 三维与轴对称气泡无量纲体积随无量纲时间的变化曲线Fig.3 Time history of bubble dimensionless volume of 3D and axisymmetrical result

1）每个小的球三角形（例如，球三角形NBC）的面积可以通过下面的积分求得［10］：

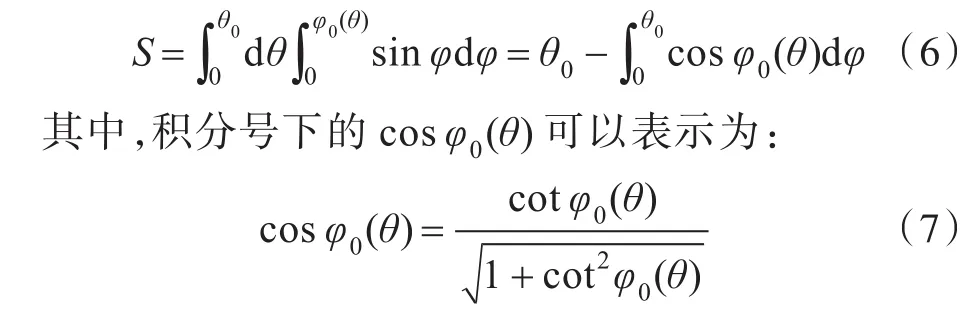
其中φ0和θ的关系可以从图4中找出。图中，点O′为边界上的结点，ON是点O′的单位法向量，弧AB，BC，CD，DE和EA分别是以 O′点为原点的单位圆与线性单元（延长线）的交界线。这样，点O′的立体角λ便可以表示为弧ANB，BNC等球三角形的面积之和。

2）边界立体角可通过如下方法求解［11］：

式中，Nb为结点 p周围三角形的个数；δi为两个相邻三角形单元的角度。

2 数值结果

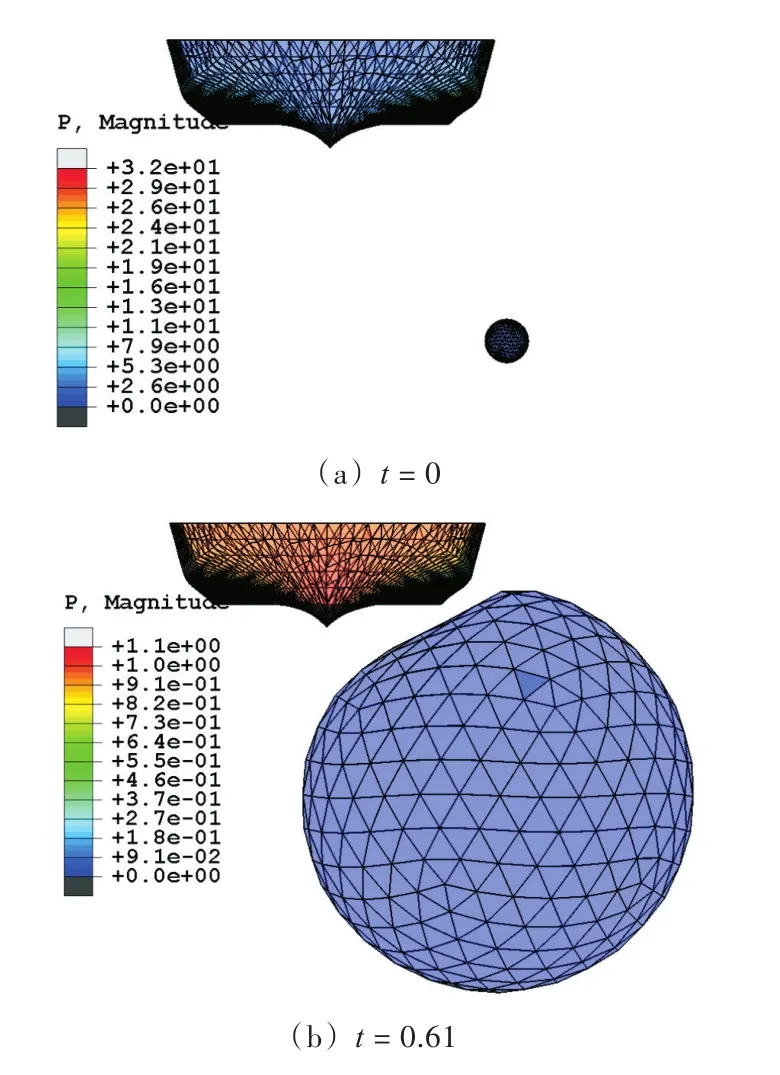
本文计算气泡的代码采用Fortran语言编写，采用有限元软件ABAQUS进行后处理，以实现计算过程可视化。考虑初始质量为N kg TNT的药包安置在船体正下方0.4L的位置。气泡脉动过程如图5所示。图5（a）为初始气泡，在气泡内部充满了高温高压气体，随后气泡迅速膨胀，在船体表面中部压力最大。在t＝0.51时刻，气泡体积达到最大然后便开始坍塌，在t＝1.04时刻，气泡开始产生向上的射流，在t＝1.08时刻，环状气泡形成，并在t＝1.11时刻体积达到最小。不同时刻舰船表面的压力分布如图6所示。由图中可看出，在t＝0的初始时刻和环状气泡体积最小的时刻（t＝1.11）附近，短时间内船体表面承受的垂向载荷数值很大，对舰船表面产生了类似“中拱”的巨大力矩，这时，结构处于危险状态。在其余的绝大部分时间内，舰船表面的垂向载荷均很小。

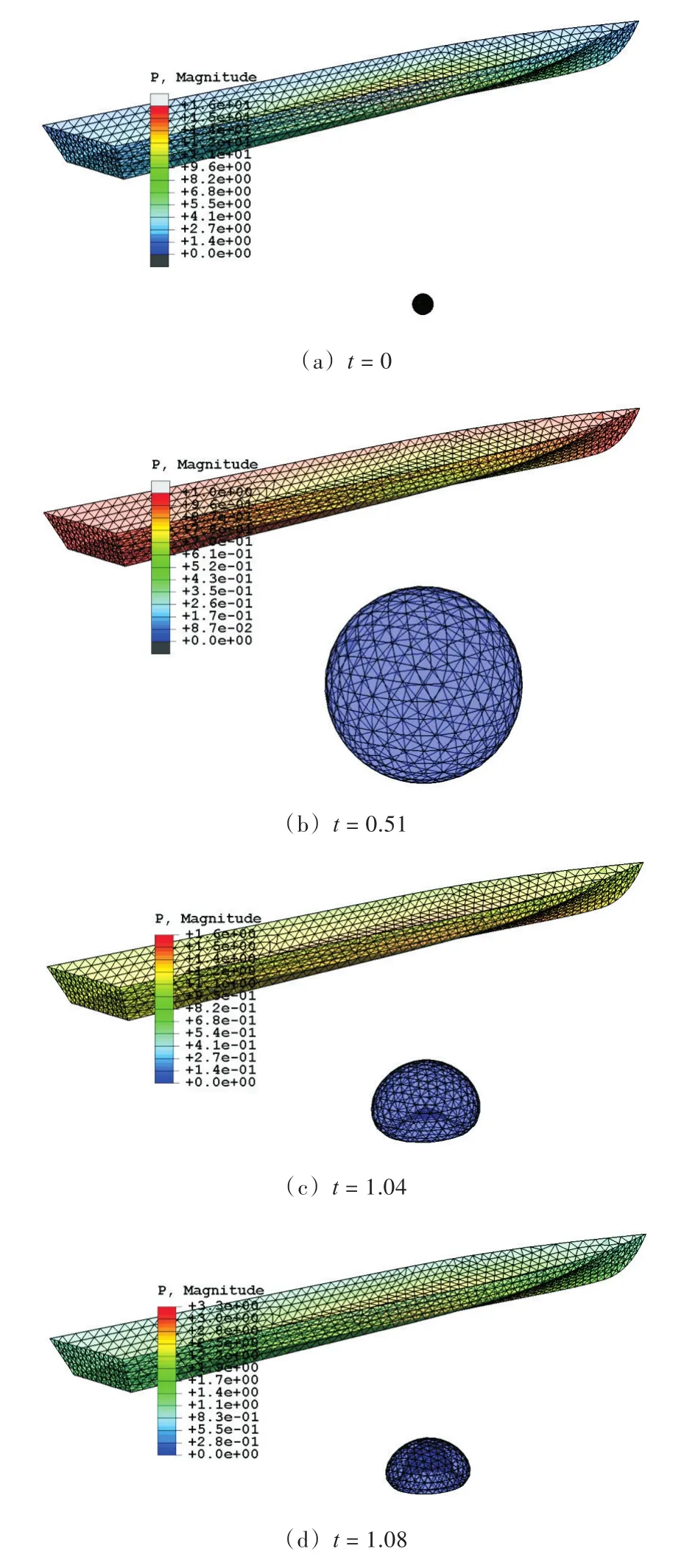
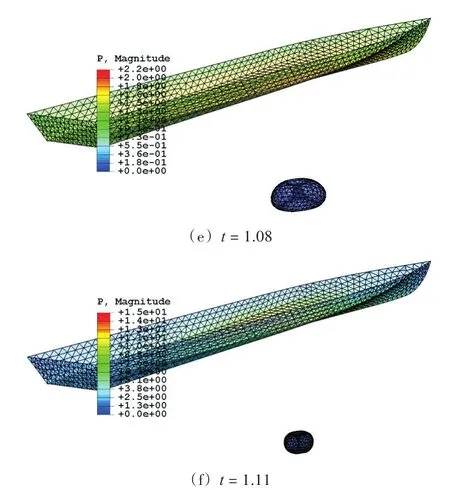
图5 N kg TNT药包距离水面0.4L爆炸生成气泡的动态特性Fig.5 Bubble dynamics generated by N kg TNT at 0.4L depth

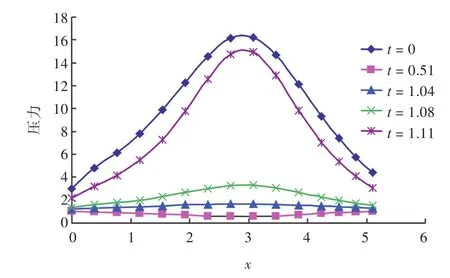
图6 舰船表面沿船长方向的无量纲垂向载荷分布Fig.6 Dimensionless vertical load distributing on ship surface

舰船表面中点的气泡载荷时历曲线如图7所示。舰船遭受气泡作用的载荷与气泡本身的运动息息相关，在气泡脉动的绝大部分时间内，气泡为近似球形，气泡脉动速度较慢，舰船表面始终维持着低于静水压力的压强值；在气泡初始时刻和环状气泡体积最小时刻附近，舰船遭受着危险载荷，且射流在冲破气泡壁的瞬间还会对舰船表面产生较大的射流冲击载荷，计算值为14.83。射流冲击主要是对结构造成局部性损伤，并有可能在流场中产生空化，射流冲击的特性还有待进一步的探索。

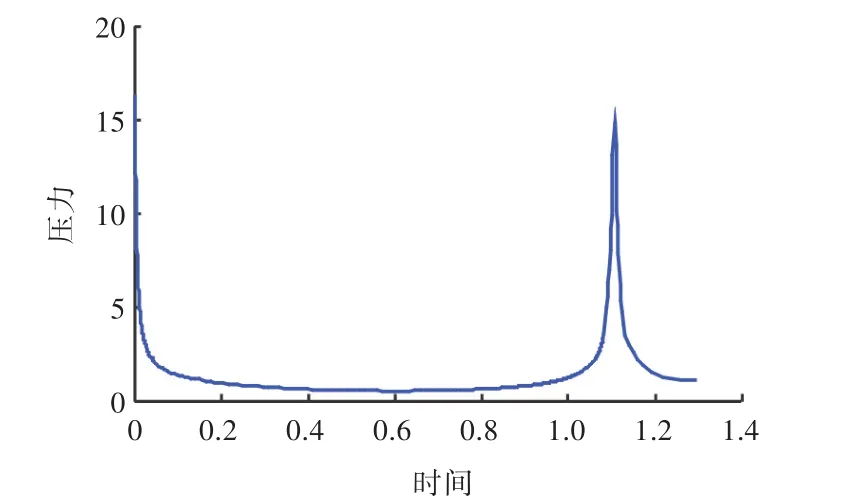
图7 舰船表面中点无量纲垂向载荷时历曲线Fig.7 Dimensionless vertical load of bubble on middle ship surface

当水下爆炸不是发生在舰船正下方，例如，发生在舷侧与水面附近时（图8），舷侧的存在使得气泡产生朝向舷侧曲面的射流，而自由面的存在又使得气泡产生朝向远离自由面的射流，在这两股影响下，气泡便产生斜向下的射流，具体实验过程参见文献［12］。因此，当药包在自由面和舷侧附近爆炸时，气泡的攻击效果会被削弱。下面，将模拟水下爆炸气泡在舷侧和自由面附近的情况，在计算过程中，采用镜像方法考虑了自由面对气泡脉动的影响。

图8 自由面附近气泡对舷侧的攻击效果Fig.8 Attack effect of bubble near shipboard and free surface

初始质量为N kg TNT的药包安置在船体正下方0.3L，左侧0.55B的位置处。气泡脉动过程如图9所示，其中，图中云图表示压力。此工况为靠近水面舰船和自由面的情况，舰船和自由面对气泡脉动的影响都很大。在此算例中，药包距离船体较近，在气泡膨胀至最大体积的过程中，舰船对气泡有阻碍作用，而在气泡坍塌的过程中，船体对其的吸引较剧烈，气泡在靠近船体一侧较大，形成了远离自由面和靠近舰船的斜射流。

初始质量为N kg TNT的药包安置在船体正下方0.3L、左侧0.8B的位置处。气泡脉动过程如图10所示，其中，图中云图表示压力。在此算例中，药包距离船体较远，受船体的吸引较小，气泡在膨胀至最大体积附近时受到了舰船轻微的排斥，而在坍塌过程中则受到了舰船的吸引。与上一算例相比，气泡被船体吸引较小，气泡射流向下。

如果水下爆炸气泡出现在水中结构物附近，通常会形成一股朝向水中结构物的射流，这股射流非常大（速度将达到100 m/s，甚至更大），并有可能会对水中结构物造成毁伤。根据气泡与水中结构物的相对位置，由于近自由面和浮力的影响，气泡射流可能会作用在水中结构物上，也有可能不会直接作用在结构上。

3 结 语

对于水面舰船，自由面的存在不仅增加了网格的数量，而且在自由面与结构的交界处也增加了数值处理的难度。本文采用考虑了自由面效应的格林函数来取代基本格林函数，计入自由面的存在对气泡运动的影响，并将计算结果与轴对称数值模拟结果进行了对比，数值结果吻合良好。

通过数值模拟和实验发现，当药包在舷侧和自由面附近爆炸时，气泡射流可能不会完全作用在舰船上，自由面效应的存在削弱了气泡的打击能力。因此，在指导常规武器攻击水面舰船时，为充分发挥气泡射流的威力，应尽量避免其在自由面附近爆炸。

［1］KLASEBOER E，KHOO B C，HUNG K C.Dynamics of an oscillating bubble near a floating structure［J］.Journal of Fluid and Structures，2005，21（4）：395-412.

［2］COLE R H.Underwater explosion［M］.New Jersey：Princeton University Press，1948：118-127.

［3］张阿漫，王诗平，汪玉，等.水下爆炸对舰船结构损伤特性研究综述［J］.中国舰船研究，2011，6（3）：1-7.ZHANG A M，WANG S P，WANG Y，et al.Advances in the research of characteristics of warship structural damage due to underwater explosion［J］.Chinese Journal of Ship Research，2011，6（3）：1-7.

［4］张阿漫，姚熊亮.近自由面水下爆炸气泡的运动规律研究［J］.物理学报，2008，57（1）：339-353.ZHANG A M，YAO X L.The law of the underwater explosion bubble motion near free surface［J］.Acta Physica Sinica，2008，57（1）：339-353.

［5］WANG Q X，YEO K S，KHOO B C，et al.Unstructured MEL modelling of unsteady nonlinear ship waves［J］.Journal of Computational Physics，2005，210 （1）183-224.

［6］ZHANG Y L，YEO K S，KHOO B C，et al.3D jet impact and toroidal bubbles［J］.Journal of Computational Physics，2001，166（2）：336-360.

［7］宗智，何亮，孙龙泉.水下爆炸气泡对水面舰船载荷的数值研究［J］.船舶力学，2008，12（5）：733-739.ZONG Z，HE L，SUN L Q.Numerical study of loading on the surface ship near an underwater explosion bubble［J］.Journal of Ship Mechanics，2008，12（5）：733-739.

［8］WANG C，KHOO B C.An indirect boundary element method for three-dimensional explosion bubbles［J］.Journal of Computational Physics，2004，194（2）：451-480.

［9］戴遗山，段文洋.船舶在波浪中运动的势流理论［M］.北京：国防工业出版社，2008.

［10］ZHANG Y L，YEO K S，KHOO B C，et al.Three-dimensional computation of bubbles near a free surface［J］.Journal of Computational Physics，1998，146（1）：105-123.

［11］WANG Q X.Numerical modelling of violent bubble motion［J］.Physics of Fluids，2004，16（5）：1610-1619.

［12］张阿漫，王诗平，白兆宏，等.不同环境下气泡脉动特性实验研究［J］.力学学报，2011，43（1）：71-83.ZHANG A M，WANG S P，BAI Z H，et al.Experimental study on bubble pulse features under different circumstances［J］.Acta Mechanica Sinica，2011，43（1）：71-83.