改进Catmull-Clark细分算法及其在船用螺旋桨设计中的应用
王艳华 苏 洲
1 海军潜艇学院,山东青岛 266042 2 河海大学机电工程学院,江苏常州 213022
0 引 言
舰艇作为各国海军的重要国防力量,其优良的生存能力是衡量技战术性能的重要指标,其中就包括提高其自身隐身性能、减小被探测到的几率的能力。与军事强国相比,目前我国海军舰艇的隐身性能依然存在着一定的差距。提高舰艇隐身性能的方法很多,其中,在涉及舰艇隐身性能的关键零件的设计制造过程中,改进设计造型方法,主动提高舰艇零件的设计制造精度,降低可能产生的噪声辐射的等级或雷达反射波等就是一项行之有效的措施[1]。学术界认为,舰艇噪声辐射已成为影响舰艇隐蔽性的主要因素[2],并且公认螺旋桨噪声是最主要的舰船噪声源[3]。但在舰船及其相关零部件的优化设计制造方面,我国目前还涉及较少。因此,在进行舰艇设计、制造时,对一些涉及舰艇隐身性能的关键零件,如螺旋桨等,有必要进行深入的声隐身性能研究,尽量使之符合降噪消音的原理,然后采用先进的造型方法,如自适应细分曲面技术来实现造型,用以在工作中就能达到降低噪声辐射的目的。在此,本文将只对其中的造型实现方法进行详细研究。
目前,国内外学者已对自适应细分造型方法进行了一定的研究,并也提出了一些行之有效的自适应细分算法和相关技术[4-8]。但这些算法在工程实践中仍然存在一定的局限性,特别是在舰艇零件设计方面的应用更少,这主要是因为现有的这些自适应方法在实现的过程中,其数值的计算受均值思想影响较重,对于控制网格光顺区域和非光顺区域的区分能力不足,从而使得部分已光顺区域网格过密。同时,对于模型中的一些尖锐特征和过渡区域,不能做出准确的判断,导致模型细分结果与极限曲面间的误差较大。本文将结合舰艇隐身性能的需要,以Catmull-Clark细分算法[9]为基础,提出一种能解决上述问题的自适应细分策略。
1 Catmull-Clark细分算法
该细分模式由Catmull和Clark于1978年提出,是一种针对以四边形网格为主的多边形控制网格的细分方法,细分曲面的极限是双三次B样条曲面,其规则包括两部分:几何规则和拓扑规则。
1.1 几何规则
C-C细分模式的几何规则主要是计算并生成控制网格的新面点、新边点和新顶点,具体细分面如图1所示。

图1 C-C细分模式几何规则Fig.1 C-C subdivision geometric rules
新面点,即F-顶点,如图1(a)所示。设原顶点分别为 v1,v2,v3,v4:

1.2 拓扑规则
C-C细分模式的拓扑规则比较简单,就是新面点和新顶点分别与新边点相连接,由此生成一张新的控制网格。
1.3 Catmull-Clark细分实验结果
利用三维建模软件3DS MAX及其内部编程语言MAXScript,即可实现原始C-C细分算法(图2),并且可以知道,模型控制网格的数量呈几何级数增长。
2 基于Catmull-Clark模式的自适应细分算法

图2 管路三通模型原始C-C算法细分结果Fig.2 Models of pipe three links based on original C-C subdivision algorithm
仔细观察图2可发现,模型控制网格的数量呈几何级数急剧增长,若模型较复杂,就会给计算机的计算、显示和存储带来极大的困难,甚至会超出计算机的能力。通过对比模型细分3次和4次的结果可以看到,经过一定次数的细分后,网格数巨增,但模型的显示效果却没有明显变化,特别是在管口处尤为明显。鉴于此,为避免均值思想对网格光顺程度带来的不利影响,提出了一种针对模型中局部网格边的基于边光顺程度(Edge Smooth Value,ESV)的自适应策略。
因四边形网格被广泛应用于各类造型系统软件中,且其相对于其它形状的网格更适于加工,能够得到高精度的加工表面[10],因而本文的算法将主要针对四边形网格。
2.1 定 义
给出了与规则相关的定义[11-12],如图3所示。

图3 基于边光顺度的自适应细分算法几何规则Fig.3 Geometric rules of adaptive subdivision algorithm based on ESV
定义1 面边三角形(Face Edge Triangle):以某个四边形网格的面片中心为一个顶点,再以该面片任意一条边的两个端点为另两个顶点连接而成的三角形,即

定义2 面边三角形的法向量(Vector):逆时针环绕面边三角形三个顶点所得到的法向量,即
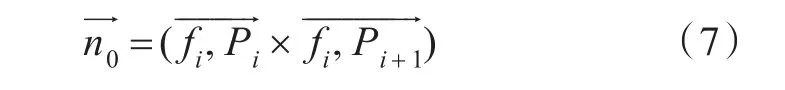
定义3 边光顺度(Edge Smooth Value,ESV):若两个面边三角形共享同一条网格边,那么其法向量的夹角就称为共享边的光顺度,即

定义4 光顺边(Smooth Edge):给定一个误差阈值εT,将计算得到的某一网格边的边光顺度与之比较,计算值小于或等于给定阈值的边就称为光顺边,计算值大于给定阈值的边就称为非光顺边。
定义5 不动顶点(No Move Vertex):对于与同一条光顺边相邻的两个面片,可以指定其上的所有顶点均为不动顶点,这些顶点在下一级细分中的几何位置保持不变。
定义6 不动面片(No Move Face):对于控制网格中的某一面片,若其所有顶点都是不动顶点,则称该面片为不动面片。此定义也包括在网格中,与某一条光顺边相邻的面片即为不动面片。
2.2 判 据
针对局部网格,对于任意的网格边,给定一个阈值εT,然后对网格中各条边的光顺度进行计算,并将计算值与给定阈值进行比较。当某网格边的光顺度小于或等于给定阈值时,便将此网格边标定为光顺边,也称死边(Dead Line),其顶点可以指定为不动顶点,且在下一级细分中保持几何位置不变。否则,便将该网格边标定为非光顺边,也称活边(Live Line),需要参加下一级的细分,直到每个面片均为不动面片为止。
2.3 算法的拓扑规则设计
自适应细分算法拓扑规则的建立过程如下:
Step1 对模型控制网格中所有的边进行光顺度计算,将计算结果与给定阈值进行比较并对相关几何元素的光顺性和可动性进行标记:当网格边的光顺度小于等于给定阈值时,将此边标定为光顺边,亦即死边;与此光顺边相邻的两个面片标定为光顺面,亦即死面(Dead Face);若网格中环绕某一顶点的所有面均为光顺面,则标定该顶点为死点(Dead Vertex)。
Step2 遍历控制网格的所有面片,按原始C-C细分模式生成新面点,若所遍历的某一面片为不动面片(亦即死面),则不生成新面点。
Step3 遍历控制网格的所有边,按原始C-C细分模式生成新边点,若所遍历的某一条边为光顺边,则用该边的中点代替刚生成的新边点。
Step4 遍历控制网格的所有顶点,按原始C-C细分模式生成新顶点,若所遍历的顶点为不动顶点(亦即死点),则直接用该顶点代替刚生成的新顶点。
Step5 将新顶点和新面点分别与新边点相连接,生成新的自适应细分网格。
Step6 消除网格裂缝,生成最终模型。
该算法的实现流程如图4所示。

图4 算法实现流程图Fig.4 Algorithm flow chart
为了实现本文的算法,在大型三维建模软件3DS MAX中,采用MAXScript语言进行了编程,人机交互界面如图5所示。
图5 人机交互界面截图Fig.5 Screenshots of human-computer interaction
3 数值实验结果
本文以船用螺旋桨为例(图6),通过建模软件3DS MAX及其内部编程语言MAXScript实现了所提出的自适应细分算法,并将结果与原始C-C算法的细分结果进行了对比。

图6 不同细分算法细分结果对比Fig.6 Comparison of the results based on different subdivision algorithms
螺旋桨模型的初始控制网格为1 464个四边形面片,采用原始C-C算法进行细分,一次细分后的面片数就达到了5 856个,并且由图6(b)可以看到,此种细分方式的每一次细分过程都是全局均匀细分,网格数增长非常快,并且已经光顺的区域仍参加下一次的细分,致使计算机的负担很重。
而采用本文提出的自适应细分算法对模型进行自适应细分,当边的光顺度阈值取为0.5时,便可以较准确地将已光顺区域从整个网格中区分出来,这样就可使细分过程只针对未光顺区域进行,其细分针对性更强,最终得到了4 506个面片(图6(c)),相比原始算法,网格数降低了约 23.05%;当边的光顺度阈值取为0.825时,可得到更少的控制网格数,为4 168(图6(d)),相比原始算法,网格数降低了约28.83%,大大提高了计算机的运算、存储和显示速度,减小了存储空间。
对于采用本文算法设计的模型能否满足舰艇在降噪消音、推进功率、零件强度和刚度等方面的需求,已专门利用相关的分析软件ANSYS,FLUENT等对模型进行了力学、流体力学等相应的数值分析,验证了算法的正确性和可行性,本文在此不再赘述。
4 不同自适应算法对比分析
表2所示为采用传统顶点曲率自适应细分一次和采用本文自适应细分一次的结果对比。

表2 不同自适应细分算法细分数据对比Tab.2 Comparison of data based on different adaptive subdivision algorithms
如图7所示,模型中圆圈所标示的范围即为采用不同的算法得到的细分结果。通过对比可以发现:采用传统的顶点曲率判别方法对模型进行自适应细分,由于顶点曲率的计算过程受均值思想的影响,在桨叶较光顺的区域网格密度仍较大,而在桨叶边缘等高曲率区域(或过渡区域),其网格密度与叶片表面较光顺区域的加密密度几乎没有差别,模型过渡特征不突出,被均匀化了;而与传统的曲率判别方法相比,在网格数量降低程度相当的情况下(数据对比见表2),采用本文的方法则能较准确地区分已光顺区域和未光顺区域(光顺区域的网格密度明显减小),能准确地捕捉到桨叶的过渡特征(例如,桨叶边缘等高曲率处),然后便可有针对性地适当加大该处网格的细分密度,满足造型的光顺性需求,最终使模型造型更合适。
结合表2和图7可得出结论:在网格数下降相当的情况下,采用本文的自适应算法对模型进行细分,细分过程更具针对性,模型高曲率区域的细分能得到加强,网格密度进一步加密,模型造型更加合理。
有关如何对该自适应细分算法进行误差控制和精度分析,以及算法能否应用于其它细分模式和网格等问题,可作为下一步研究的重点。
5 结 论
在认真研究现有自适应细分技术的基础上,本文结合舰艇的隐身性能需求,提出了将自适应细分技术应用于舰艇关键零件设计和制造的工程实际,并以Catmull-Clark细分算法为基础,针对四边形网格提出了基于网格边光顺度计算的自适应细分方法,同时还以船用螺旋桨为例进行了数值实验。从实验结果可得到如下结论:
1)算法能较好地降低网格数量;
2)对于网格中的光顺区域和非光顺区域,该算法具有较强的区分能力;
3)对于控制网格中的尖锐特征或曲率较高的过渡区域,该算法具有较强的捕捉能力,能进一步加大这些区域的控制网格的密度,以使整个细分过程更具针对性,从而有效避免以顶点曲率等为判断阈值的均值思想所带来的对网格几何特征区分能力不足的不利影响。
[1]龚锦伟,王振民,王立新,等.舰船隐身设计探讨[J].船舶,2003(3):29-31,62.GONG J W,WANG Z M,WANG L X,et al.Discussion on naval ship stealth[J].Ship and Boat,2003(3):29-31,62.
[2]缪旭弘,王振全.舰艇水下噪声控制技术现状及发展对策[C]//第十届船舶水下噪声学术讨论会论文集,2005.
[3]杨琼方,王永生,张明敏.舰艇螺旋桨水下噪声预测[J].船舶力学,2011,15(4):435-442.YANG Q F,WANG Y S,ZHANG M M.Underwater noise prediction of ship and submarine propeller[J].Journal of Ship Mechanics,2011,15(4):435-442.
[4]AMRESH A,FARIN G,RAZDAN A.Adaptive subdivision schemes for triangular meshes[C]//Hierarchical and Geometric Methods in Scientific Visualization.Berlin:Springer-Verlag,2003:319-327.
[5]HU H P,ZHAN Q,JIANG H B,et al.Adaptive refinements in Catmull-Clark subdivision scheme[J].Journal of Huazhong University of Science and Technology(Nature Science Edition),2002,30(10):56-58.
[7]CHENG K S D,WANG W P,QIN H,et al.Fitting subdivision surfaces to unorganized point data using SDM[C]//Proceedings of the 12th Pacific Conference on Computer Graphics and Application(PG’04).Seoul,2004:16-24.
[8]WU J H,LIU W J,WANG T R.Adaptive refinement scheme for subdivision surfaces based on triangular meshes[C]//Proceedings of the Ninth International Conference on Computer Aided Design and Computer Graphics(CAD-CG’05),2005:119-124.
[9]CATMULL E,CLARK J.Recursivelygenerated B-spline surfaces on arbitrary topological meshes[J].Computer-Aided Design,1978,10(6):350-355.
[10]赵建民.基于Catmull-Clark模式的细分曲面NC刀具轨迹生成技术[D].大连:大连理工大学,2008.
[11]郑津津,朱巍,周洪军,等.非平均化自适应catmull-clark细分算法[J].计算机应用与软件,2010,27(1):6-8,22.ZHENG J J,ZHU W,ZHOU H J,et al.Non-uniform adaptive catmull-clark subdivision algorithm[J].Computer Applications and Software,2010,27(1):6-8,22.
[12]朱巍.细分曲面理论及其应用问题的研究[D].合肥:中国科学技术大学,2011.

