船舶结构理性设计方法热点问题与展望

孙 利 王德禹

1 上海交通大学船舶海洋与建筑工程学院，上海 200240 2 中国船舶及海洋工程设计研究院，上海 200011

0 引 言

随着运输成本的上升以及运输产品的种类增加，船舶日益向尺度大型化、种类多样化的方向发展。以集装箱船为例，其载货量的变化历经上世纪60年代的700～1 000 TEU，70年代的1 800～2 000 TEU，1973年以后的3 000 TEU，80年代后期的4 400 TEU，直至目前发展到8 000 TEU，9 000 TEU甚至是万箱货船。随着尺度的不断增大，对于船舶结构的强度提出了更高的要求。由于船舶尺度增加，波激振动和振颤等问题也变得十分显著，需要设计者特别注意。目前，船舶的种类日益增加，如常见的散货船、油船、集装箱船、LNG船和FPSO等。不同种类的船舶在设计时有许多特殊的因素需要考虑，如油船和LNG船需要考虑晃荡问题，大型集装箱船需要注意弯扭组合作用下的强度，FPSO等超大型储油船舶对安全性提出了更高的要求等。此外，人们对于船舶设计有了更多的要求，如安全性、经济性和快速性等。安全性始终是船舶设计者首先要实现的目标，但在满足安全性要求的基础上，尤其对于商用船舶而言，设计者也更加重视设计方案的经济性。而在进行军用船舶的设计时，对于安全性和快速性等指标则更为关心。

以上这些船舶形式、大小上的变化以及人们对船舶设计要求目标的多样化，使得原本单纯依赖于设计者主观经验或船级社颁布的规范所规定的最小尺寸的传统设计方法难以满足现代船舶设计的需要。传统设计方法应用方便简单，使用者根据规范规定的公式、最小尺寸等便可以快速得到设计方案。但是，这种方法存在以下3个缺点：

1）由于船舶结构的失效形式有很多种，单纯依赖公式来解决所有失效问题必然导致设计者无法判别针对每种失效形式所设计结构的精确冗余度，这样的设计势必难以保证高效性。

2）规范给出的公式、要求和最小尺寸等都是为了设计出的船舶结构可以避免结构失效，但由于船东或设计者对于船舶结构设计有了更全面的要求，仅仅满足结构的安全性是不够的。

3）规范所给出的要求大多是有使用范围的，但随着船舶尺度的增大或新船型的出现，设计者可能难以找到可以应用的规范作为参考。即使在规范使用范围之内，如果比较靠近范围上限，这些规范公式的可信性也值得怀疑。

针对传统设计方法的不足，Hughes［1］将航空领域的设计理念“理性设计方法”引入船舶结构设计中。理性设计方法是一种直接并完全以结构理论和基于计算机技术的结构分析和优化为基础的、最终依赖设计者选择出优化的设计结构的方法。理性设计方法有以下几个主要特点：

1）完全以结构理论而非经验公式为基础；

2）依托计算机技术，应用数值方法进行计算分析；

3）依托计算机技术，依赖优化算法和优化策略寻找最优设计；

4）设计者可以自由选择各项设计性能的权重。

理性设计方法主要由3项任务组成，即分析计算、设计评价以及优化。

分析计算主要包括对于船舶所受环境载荷的计算、船体各个结构受环境载荷作用下的结构响应Q，在船体所能承受的极限载荷作用下船体各个结构的结构响应QL以及基于可靠性理论求得各类分部安全系数γ。

设计评价主要包括两个方面，即约束条件是否满足以及设计结果是否达到最优。约束条件主要包括强度约束和非强度约束。强度约束是基于可靠性理论对结构响应Q加以限制，如式（1）所示。强度约束的目的是保证船舶有足够的安全性和可用性，而非强度约束主要指由于施工建造需求以及使用的需求等对结构的尺寸形状等有所限制。

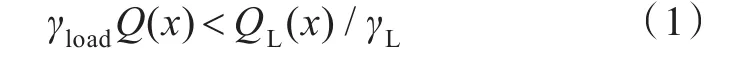
式中，x为主要结构的编号；γload和γL均为安全系数，分别为载荷系数和极限强度系数［1］。

评价设计结果是否达到最优必然需要评价标准，即优化问题中的目标函数。以民用船舶为例，经济性应该是船东或设计者最希望改进的优化目标。而影响经济性的参数主要包括空船重量、高强度钢的使用量、建造施工的难度、船舶的快速性以及是否低能耗等。除了经济性以外，船员的生活、工作环境也越来越受到人们的重视。因此，船舶耐波性和振动噪声等性能也是重要的衡量指标。当然，对于不同指标在优化问题中有不同的处理方式，设计者可以把某项指标作为目标函数，也可以给定容许边界将其设定为约束条件处理。然而，在实际设计中，除了规范限定的出于安全性考虑强制要求的指标有明确的上、下限要求（如许用应力、最大位移和最大振动响应等）外，其他许多指标都是十分感性而难以确定约束边界的。因此，许多时候设计者需要考虑多种评价标准并最后由船东或设计者选出偏好的设计方案。随着现代船舶的优化设计向多目标优化问题发展，涉及的学科繁多（包括经济、结构、流体、建造等），多学科优化问题也越来越受到船舶结构设计、研究人员的关注。

通过前述分析可知，分析计算的目的是为设计评价提供数据依据、设计评价则是为优化问题建立数学模型，而理性设计方法的核心就是利用优化策略和优化算法针对此前的数学优化模型选出最优的结构尺寸、结构形状、拓扑结构以及经济性更好的结构材料等。

下面将根据理性设计方法的特点介绍其在船舶设计领域应用时表现出的问题以及相关研究的情况，而后重点针对船舶结构多学科多目标优化设计这一热门领域的发展情况进行介绍，最后，展望理性设计方法应用于船舶设计领域的前景。

1 理性设计方法热点问题

1.1 计算成本

理性设计方法主要依赖于以计算机技术为载体的数值计算方法进行计算分析，并且以优化迭代作为寻找最优设计方案的方法，因此，应用理性设计方法对船舶这一大型的复杂结构进行设计的时间成本将非常高。首先，对于复杂的大型结构而言，应用FEM，CFD等数值计算方法需要的计算时间相当可观；其次，由于应用优化算法，随着设计变量数量和种类的增加、约束条件增加、以及随着优化问题的非线性化增强，优化迭代的步数将会大幅增加，从而需要进行大量的重复计算，进而导致累积起来的计算成本更高；最后，由于当今船舶设计已不再限于单目标、单一学科，而是一个多目标、多学科的综合性问题，这也势必导致需要更多的优化步数和更高的单步计算成本。

针对上述问题，目前主要可以遵循3种思路予以解决，即结构分解、“大”单元和元模型。

1.1.1 结构分解

将船舶按结构部位划分成多个子系统（子模块），从系统层面对各子系统进行协调，而各个子系统独立进行计算、分析以及优化。大型复杂结构一旦被分解成若干子结构，无论是该子系统的设计变量还是结构模型的分析时间，都将大幅减少。

Hughes等［2］首先提出了船体模块的概念以及基于船体模块概念的多级分析理念。Rahman［3］结合总体目标协调方法（General Goal Coordination Method）将船体梁分解为甲板、舷侧和船底等子结构并进行了多级分析优化设计。按照结构部位将船舶分解后，进行分级计算优化时存在一个重要问题，即如何处理子结构或船体模块的边界条件，Hughes提出的方法是将船体梁模型作为整船分析对象，然后将船体梁模型计算得到的节点位移传递到船体模块的两端边界，即认为船体模块两端各节点位移是相同的。该方法仅适用于两端结构刚度较强（通常以横舱壁为边界）的船体模块，而对于横舱壁较少的船舶势必将导致船体模块很大，计算成本无法明显减少。Sun和Wang［4］提出了结合超单元技术处理船体模块的边界条件，该方法无需要求船体模块以横舱壁为边界，提高了多级分析方法的灵活性。

1.1.2 “大”单元

利用结构理论，将复杂多自由度的有限元模型以近似的低自由度的“大”单元模拟代替。船舶结构的数值分析主要依赖于有限元方法，然而该方法的计算成本与单元节点的数量成正比关系，采用少量的“大”单元代替数量繁多的精细单元可以显著缩短计算时间。这里的“大”单元包括Hughes提出的宏单元（Macro Element），Satish［5］研究的新式加筋板单元以及Naar等［6］研究的耦合梁等。此外，以宏单元和粗单元（Gross Element）为模块，Andric［7］提出了在船舶概念设计阶段的通用船体模型（Generic Ship Model）理念。这些“大”单元可以快速地为设计者提供近似的分析结果。

1.1.3 元模型

元模型（Metamodel）是指基于回归方法或数理统计理论，可以近似模拟复杂数值分析程序的输入—输出关系的数学模型。由于元模型多基于简单的数学模型，所以其计算成本相当低。以前需要数小时甚至几天完成的数值分析程序，现在仅需数秒即可得到相近的结果。Wang［8］系统地介绍了元模型在工程优化设计领域的应用与发展情况。

比较常用的元模型包括响应面法（Response Surface Methodology，RSM），泰勒级数法（Taylor Series），随机模型（Kriging Model），径向基函数法（Radial Basis Functions，RBF）以及基于机器学习方法的人工神经网络法（Artificial Neural Network，ANN）。

马斯里亚说，几年前，NIH用于研究阿尔茨海默病的资金中，大部分用在β-淀粉样蛋白和tau蛋白研究领域，现在60%多的资金用于转化研究，大约70%的资金用于基础研究。北卡罗来纳州杜克大学的卡罗尔·科尔顿（Carol Colton）说：“我相信我们会有更多的资金来探索其他的想法。”科尔顿正在将炎症作为阿尔茨海默病的潜在原因进行研究。然而，她和其他研究人员补充说道：“一些学者呼吁重新审视NIH的拨款提议，有时他们的思想不如国家老龄化研究所的员工那么开放，他们拒绝新领域研究的申请，他们需要转变观念。”

上述方法中，RSM应用广泛，它利用低阶多项式回归拟合给定的输入—输出值［9］。Arai和Suzuki等［10-11］在船舶横舱壁的结构优化中应用了RSM法。对于高维非线性问题，RSM方法的准确性和稳定性均大幅降低［12］。Sacks等［13］提出使用 Kriging Model来模拟确定性的计算程序。相较RSM方法，Kriging Model方法对于非线性问题的计算更为准确。但对于高维问题，由于它需要处理复杂的矩阵求逆等运算，因此使用成本也很高。

ANN方法以已知输入—输出关系为训练样本，以某种训练机制（如反向传播Back Propagation，BP）更新其数学结构，训练后得到的数学结构即为输入—输出关系的模拟器。常用ANN包括多层感知器（Multi-Layer Perceptron，MLP）和基于径向基函数的神经网络（Radial Basis Function Network，RBFN）等［14］。邵雄飞［15］应用 RBFN 方法对大型油船三舱段模型进行了结构优化。但ANN方法受网络结构复杂性和样本复杂性的影响较大，容易出现“过学习”或低泛化能力。

传统的ANN方法的重要理论基础之一是统计学。传统统计学研究的是样本数目趋于无穷大时的渐近理论，现有学习方法也多是基于此假设。但在解决实际问题时，样本数量往往是有限的，因此一些理论上很优秀的学习方法在实际应用中的效果可能不尽人意。与传统统计学相比，统计学习理论（Statistical Learning Theory，SLT）是一种专门研究小样本情况下机器学习规律的理论，在该理论基础上发展了一种新的通用学习方法——支持向量机（Support Vector Machine，SVM），它是一种比较好的实现了结构风险最小化思想的方法。它的机器学习策略是结构风险最小化原则，其目的是最小化期望风险，应同时最小化经验风险和置信范围［16］。由于SVM方法与传统的学习机同样难以获得输入输出关系的梯度，因此应用SVM方法的优化问题并不适合应用基于梯度的传统优化算法。将SVM方法与遗传算法（Genetic Algorithm，GA）相结合的优化方法也是研究的热点之一［17-18］。

1.2 参数化建模

由于理性设计方法主要基于计算机技术、调用优化算法自动迭代完成建模、分析和判断等工作，因此要求上述几项工作完全可以由计算机自动完成，无需人工干预。计算分析和判断工作早已有成熟的数值计算软件（如Nastran，Ansys，Fluent等）和优化平台（如iSIGHT，Optistruct等）实现，而对于自动建模问题，至今仍是一个难点。现在各大数值计算软件的前处理工具均融合了强大的编程功能，为使用者参数化建模提供了很好的平台，如Patran的PCL语言，Abaqus的Python语言以及Ansys的APDL语言等。冯国庆等［19］研究了应用PCL语言对散货船直接强度进行评估，窦培林等［20］研究了通过 AutoCAD，VBA 和 PCL语言将Tribon模型几何信息导入Patran平台自动建模的方法。张丽［21］应用PCL语言实现参数化修改结构尺寸，对巴拿马型集装箱船的尺寸进行了优化。曾文源［22］研究了ADPL语言对于船舶结构形状优化的应用，以及采用交互式方式实现利用PCL语言参数化建立船体中间舱段的几何模型并划分网格。

然而，由于船舶结构的形状很不规则且大多数值计算软件的网格节点都要求协调匹配，这样就为复杂模型完全自动划分网格技术的实现带来了很大障碍。秦洪德等［23］详细总结了船舶在尺寸、形状和拓扑优化等方面研究的进展，此处不再赘述。

2 船舶结构理性设计方法的工程应用与展望

虽然对于理性设计方法在船舶领域的研究已经开展得很多，但是在实际设计过程中，很少有设计者会采用理性设计方法，分析其原因主要有模型问题、设计者的重要性、计算成本、参数化建模以及优化算法等。

2.1 模型问题

所有的优化算法都是基于由实际问题转化得到的数学模型。然而，在工业领域缺少熟练掌握建立这些数学模型的设计者，也没有十分成熟的商业软件供使用者完成数学建模工作，导致设计者对于这种不熟悉的模型没有充足的信心，他们更喜欢可以确切地掌握设计的每一步改善而非抽象的数学模型。

2.2 设计者的重要性

2.3 计算成本

根据前述分析可知，基于理性设计方法的计算成本相当高，这在很大程度上阻碍了其在实际设计中的应用。为解决这一问题，一方面可以利用前面提到的近似模型来模拟并代替准确但费时的计算模型；另一方面网格计算机和分布式计算技术的应用也从一定程度上解决了大规模优化问题的计算成本问题［26-27］。

此外，量子计算是一种新型的计算方式，它可以提供更快更有效的计算平台。目前，关于将量子计算手段和遗传算法［28］或群体智能［29］相结合的优化技术的相关研究工作也已经展开。

2.4 参数化建模

在实际设计工作中，设计对象多为几何模型甚至是简单的几何尺寸，如结构的形状、尺寸和材料或船舶的主尺度等。然而理性设计方法中对设计的评价往往基于数值模型，在船舶设计中最常用的数值模型包括结构有限元模型、流体方面的CFD模型等。由于目前尚无较成熟的接口或软件可以实现几何模型或几何尺寸与数值计算模型的全自动转换，这对设计者使用理性设计方法带来了很大不便。

2.5 选择合适的优化算法

成熟的优化算法有很多，如何针对不同问题选择合适的优化算法对于设计者而言是一项很复杂的挑战。虽然很多优化平台针对不同设计问题为使用者提供了优化算法的选择建议，如iSIGHT和Optistruct等，但采纳这些建议的结果大多是缩小可选优化算法的范围，而使用者仍需要根据知识经验在小范围的优化算法中选取合适的算法。此外，没有一个优化问题会仅有一种最优的优化算法，即每种优化算法对于某种特定的问题都有其优点与缺陷，因此仍然需要使用者合理地进行选择［30］。

2.6 培 训

使用传统设计方法的设计者对于理性设计方法、优化算法、可靠性方法以及近似模型的原理等都缺乏足够的知识，这很大程度上阻碍了他们对于理性设计方法应用的兴趣。因此，有必要对设计者进行相关知识的普及和推广培训。

3 结 语

尽管船舶结构理性设计方法在实际应用中面临很多问题，然而，考虑到现代船舶设计所面临的挑战，船东对于高性能、低能耗的要求以及船舶市场竞争的日趋激烈，不难得出掌握并最大限度地应用船舶结构理性等因素设计方法对于提升船舶设计水准、提高船舶结构的安全性和降低钢材原料使用成本等方面均能发挥重要的作用这一结论。

［1］HUGHES O F.Ship structural design：a rationallybased，computer-aided，optimization approach［M］.New York：Wiley，1983.

［2］HUGHES O F，MISTREE F，ZANIC V.Practical method for the rational design of ship structures［J］.Journal of Ship Research，1980，24（2）：101-113.

［3］RAHMAN M K.Multilevel optimization applied to hull girder design using three panel forms［J］.Structural and Multidisciplinary Optimization，1994，7（1）：126-137.

［4］SUN L，WANG D Y.A new rational-based optimal design strategy of ship structure based on multi-level analysis and super-element modeling method［J］.Journal of Marine Science and Application，2011，10（3）：272-280.

［5］SATISH K Y，MUKHOPADHYAY M.Finite element analysis of ship structures using a new stiffened plate element［J］.Applied Ocean Research，2000，22（6）：361-374.

［6］NAAR H，VARSTA P，KUJALA P.A theory of coupled beams for strength assessment of passenger ships［J］.Marine Structures，2004，17（8）：590-611.

［7］ANDRIC J，ZANIC V.The global structural response model for multi-deck ships in concept design phase［J］.Ocean Engineering，2010，37（8/9）：688-704.

［8］WANG G G，SHAN S.Review of metamodeling techniques in support of engineering design optimization［J］.Journal of Mechanical Design，2007，129：370-380.

［9］JONES D R，SCHONLAU M，WELCH W J.Efficient global optimization of expensive black-box functions［J］.Journal of Global Optimization，1998，13（4）：455-492.

［10］ARAI M，SHIMIZU T，SUZUKI T.Optimization of transverse bulkhead design by response surface methodology［J］.Journal of the Kansai Society of Naval Architects，Japan，2000（234）：237-244.

［11］SUZUKI T，ARAI M，SHIMIZU T.On the application of Response Surface Methodology to the optimization of ship structural design［J］.ClassNK Technical Bulletin，2001，19：39-47.

［12］GOU P，LIU W，CUI W C，A comparison of approximation methods for multidisciplinary design optimization of ship structures［J］.Journal of Ship Mechanis，2007，11（6）：913-923.

［13］SACKS J.Design and analysis of computer experiments［J］.Statistical Science，1989，4（4）：409-423.

［14］SIMON S，HAYKIN.Neural networks：a comprehensive foundation［M］.London：Prentice-Hall，1999.

［15］邵雄飞.基于直接计算的大型油船结构优化设计［D］.镇江：江苏科技大学，2007.

［16］VAPNIK V.Statistical learning theory［M］.New York：Wiley，1998.

［17］NANDI S.Hybrid process modeling and optimization strategies integrating neural networks/support vector regression and genetic algorithms：study of benzene isopropylation on Hbeta catalyst［J］.Chemical Engineering Journal，2004，97（2/3）：115-129.

［18］吕勇波.基于支持向量机与遗传算法的结构优化研究［D］.武汉：华中科技大学，2007.

［19］冯国庆，赵楠，任慧龙，等.基于PCL的散货船直接强度评估系统开发［J］.船海工程，2011，40（2）：5-8.FENG G Q，ZHAO N，REN H L，et al.Development of direct strength assessment system for bulk carrier based on Patran command language［J］.Ship and Ocean Engineering，2011，40（2）：5-8.

［20］窦培林，胡礼明.基于TRIBON数据快速建立全船有限元模型的研究［J］.船舶工程，2009，31（5）：44-46，51.DOU P L，HU L M.Study on quick finite element modeling of the whole ship based on the TRIBON data［J］.Ship Engineering，2009，31（5）：44-46，51.

［21］张丽.巴拿马型集装箱船结构优化设计研究［D］.上海：上海交通大学，2008.

［22］曾文源.舰船结构有限元参数化建模与优化研究［D］.哈尔滨：哈尔滨工程大学，2005.

［23］秦洪德，王艳艳.船舶结构优化设计的研究进展［C］//船舶力学学术会议暨《船舶力学》创刊十周年纪念学术会议.银川，2007.

［24］BRINTRUP A M，RAMSDEN J，TIWARI A.An interactive genetic algorithm-based framework for handling qualitative criteria in design optimization［J］.Computers in Industry，2007，58（3）：279-291.

［25］ZIMMERMANN M，BRONSART R，STENZEL K.Knowledge based engineering methods for ship structural design［C］//12th International Conference on Computer Applications in Shipbuilding（ICCAS），2005.

［26］GRAUER M，BARTH T，THILO F.Grid-based computing for multidisciplinary analysis and optimization［C］//10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference，2004.

［27］KERE P，LENTO J.Design optimization of laminated composite structures using distributed grid resources［J］.Composite structures，2005，71（3/4）：435-438.

［28］WANG L，TANG F，WU H.Hybrid genetic algorithm based on quantum computing for numerical optimization and parameter estimation［J］.Applied Mathematics and Computation，2005，171（2）：1141-1156.

［29］WANG L，NIU Q，FEI M.A novel quantum ant colony optimization algorithm and its application to fault diagnosis［J］.Transactions of the Institute of Measurement and Control，2008，30（3/4）：313-329.

［30］WOLPERT D H，MACREADY W G.No free lunch theorems for optimization［J］.IEEE Transactions on Evolutionary Computation，1997，1（1）：67-82.