弱耗散均匀回旋介质椭圆柱体的电磁散射
毛仕春, 王 帆
(宿迁学院 基础教学部, 江苏 宿迁 223800)
弱耗散均匀回旋介质椭圆柱体的电磁散射
毛仕春, 王 帆
(宿迁学院 基础教学部, 江苏 宿迁 223800)
分析了弱耗散型均匀回旋介质椭圆柱体的电磁散射特性.基于平面波谱的积分方程以及马丢函数的级数展开式,以横电型(TE)平面波为例,导出了弱耗散均匀回旋介质椭圆柱内场及其单位长度的雷达散射截面(RCS)的表达式.为了解决马丢函数子程序计算复数的难题,采用泰勒级数的一级近似将复数转换为实数运算.计算了部分数值并讨论了弱耗散介质对雷达散射截面的影响.
电磁散射; 椭圆柱体; 弱耗散介质材料; 马丢函数
0 引言
回旋介质是各向异性介质的一种特殊情况,而诸如等离子体、铁氧体等材料都是一种回旋介质.等离子体是由电子、中子、离子和中性分子组成的混合气体,存在于空间电离层、微波实验室等环境周围,并被广泛应用于环境目标的隐身技术等方面.例如,学者 Matsumoto采用共轭梯度快速傅里叶变换法分别研究了二维有损、非均匀磁化等离子体柱对入射平面波的散射,并给出了散射截面、回波宽度和吸收功率密度的数值结果[1];学者Hunsberger利用时域有限差分法分析了磁等离子体的电磁特性[2].由于回旋介质材料的广泛应用,回旋介质材料的电磁特性成为近年来许多学者的研究焦点之一[3-5].

图1 二维椭圆柱坐标系示意图
学者Yeh最早对介质椭圆柱的散射特性进行了讨论[6], 并计算了单位长度的雷达散射截面[7]. 随后的几十年,许多学者对导体涂覆多层介质椭圆柱的散射展开了研究[8-13]. 从已知的文献可以看出,对于均匀回旋介质椭圆柱体的散射国内外的报道较少,而对于弱耗散类回旋介质椭圆柱体的散射尚未报道.本文利用平面波谱的积分方程,在椭圆柱坐标系下, 利用马丢函数级数积分展开,得到了单位长度的雷达散射截面的解析表达式,为了解决程序无法运算复数的问题,采用泰勒级数的一级近似,将复数运算转换为实数运算,较方便的解决了若耗散回旋介质椭圆柱的电磁散射问题.为方便描述,文中省略时谐因子exp(jωt).
1 电磁场分析

(1)
其中εr=ε′+jε″(ε″≪ε′),μr=μ′+jμ″(μ″≪μ′)分别表示复相对介质常数和磁导率.
1.1 椭圆柱内场表达式
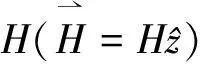

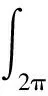
(2)
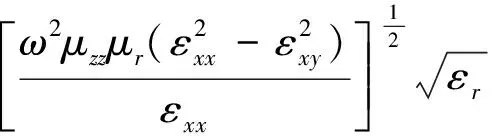
由于马丢函数复数运算的子程序尚未提供,为了解决耗散类介质的散射问题,引入泰勒级数的一级近似,即
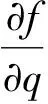
(3)

1.2 入射场和散射场表达式
假定椭圆柱体外部是理想的自由空间.振幅为H0,沿水平方向θi入射到椭圆柱体的入射场可以表示为:
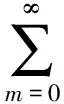
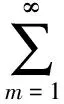
(4)
在自由空间中,假设散射场具有如下形式:
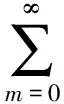
(5)
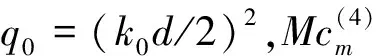
1.3 界面的切向分量
在柱体和自由空间界面上,电场在界面内侧的切向分量应满足
(6)

(7)
假设界面为u=u0,由电磁场在界面切向的连续性,则有
(8)
(9)
其中
(10)
(11)
利用Galerkin法以及上述边界条件,可得到下列两个方程组:
(12)
(13)
其中
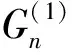
(14)

(15)

(16)

(17)
(18)
(19)
式中n=0,1,2,…,n′=1,2,3,….符号“D”表示对角向马丢函数v变量求导,或者对径向马丢函数u变量求导(或者在u=u0的导数值).
1.4 级数截断及雷达散射截面表达式
为得到数值解,必须将无穷级数进行截断.截取后通过公式(12)和(13)可求出内场以及散射场,利用径向马丢函数的渐进式,可得到单位长度的雷达散射截面(RCS):
(20)
2 数值计算
为了得到稳定的数值解,必须对无穷级数项进行截断,仅取其中的前N项.容易验证当所选椭圆柱体电尺寸较小时,N≥6时径向马丢函数的收敛性足够满足数值运算的要求.
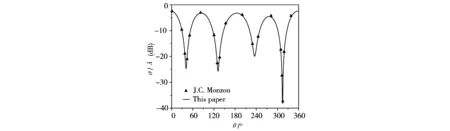
如图2所示,为了验证本节理论的正确性,利用上述散射理论将椭圆柱体退化到圆柱体时得到的结果和意大利学者Monzon[15]利用角谱积分法得到的结果吻合较好.鉴于本文理论方法与Monzon所采用的方法相互独立,从而说明了利用本文的理论方法能够较好的解释椭圆柱体的散射理论,利用和其他方法例如FDTD的数值对比也显示,其结果是正确可靠的,说明了本文理论的正确性.
图3给出了在主轴坐标系下,入射角θi=0°时,椭圆柱体弱耗散介质参数变化时雷达散射截面随散射角的变化关系.从图中可以看出雷达散射截面随着散射角呈对称分布,在前向时有最大峰值,这是由于介质系数的对称性引起的.雷达散射截面分布与椭圆柱体的电尺寸存在一定关系.相对而言,对于若耗散介质,耗散系数的变化引起的分布影响较小.
(u0=6.0,d/λ=1.24×10-3,εxx=4ε0,εxy=2jε0,μzz=2μ0,εr=1.0,μr=1.0,θi=0°.)

图3 双站雷达散射截面随散射角分布图

图4 双站雷达散射截面随散射角分布图
图4给出了介电常数张量参量εxy为复数时弱耗散介质对平面波的雷达散射截面的影响.由于参数的改变使得此时图形分布不再对称分布,但是对弱耗散介质而言,其耗散系数影响依然较小.值得注意的是,由于马丢函数子程序的限制,本文的理论适用于ε″≤0.3时的弱耗散介质情形.
3 结论
基于平面波谱的积分形式和马丢函数,得出了弱耗散均匀回旋介质椭圆柱电磁散射的积分方程并导出了单位长度的雷达散射截面.通过与已知文献的数值结果比较,理论模型能够比较真实的反映椭圆柱体电磁散射特性.计算并讨论了部分数值结果,分析了弱耗散介质参数对雷达散射截面的影响.这些结论对研究分析各向异性介质材料的散射特性有一定的参考价值.
致谢: 作者感谢Jian-ming Jin教授提供的马丢函数子程序!
[1] Matsumoto S, Okuzawa T. Scattering of a plane electromagnetic wave from magnetized cylindrical plasma[J]. Bulletin of the University of Electro-Communications,1988, 1(1): 23-30.
[2] Hunsberger F, Luebbers R, Kuru K. Finite-Difference Time-Domain Analysis of Gyrotropic Media-I: Magnetized Plasma[J]. IEEE Trans. Antennas Propagat,1992, 40(12): 1489-1495.
[3] Geng Y L, Wu X B, Li L W. Analysis of electromagnetic scattering by a plasma anisotropic sphere[J]. Radio Sci,2003, 38: 11041-11052.
[4] Yang J, Li, L W, Liang C H. Two-Dimensional Scattering by a Periodic Array of Gyrotropic Cylinders Embedded in a Dielectric Slab[J]. IEEE Trans Antennas wireless Propagat Lett,2003, 2: 18-21.
[5] Qiu C W, Li L W, Yeo T S. Field representations in general gyrotropic media in spherical coordinates[J]. IEEE Antennas wireless Propagat Lett,2005, 4: 467-470.
[6] Yeh C. The diffraction of waves by a penetrable ribbon[J]. J Math Phys,1963, 4: 65-71.
[7] Yeh C. Backscattering cross section of a dielectric elliptic cylinder[J]. J Opt Soc Am,1965, 55: 309-314.
[8] Richmond J H. Scattering by a conducting elliptic cylinder with dielectric coating[J]. Radio Sci,1988, 23: 1061-1066.
[9] Ragheb H A, Shafai L. Electromagnetic scattering from a dielectric-coated elliptic cylinder[J]. Can J Phys,1988, 66: 1115-1122.
[10] Caorsi S, Pastorino M, Raffetto M. Electromagnetic scattering by a multilayer elliptic cylinder under transverse-magnetic illumination: Series solution in terms of Mathieu functions[J]. IEEE Trans Antennas Propagat,1997, 45(6): 926-935.
[11] Caorsi S. Pastorino M. Scattering by multilayer isorefractive elliptic cylinder[J]. IEEE Trans Antennas Propagat,2004,52:189-196.
[12] Sebak A R. Scattering from dielectric-coated impedance elliptic cylinder[J]. IEEE Trans Antennas Propagat,2000, 48(10): 1574-1580.
[13] 葛俊祥,林为干. 非共轴多层介质椭圆柱体的电磁散射:任意方向斜入射电磁波[J]. 电子学报,1995, 23(3): 20-25.
[14] Blanch G. Handbook of Mathematical Functions[M]. New York: Dover, 1965: 721-746.
[15] Monzon J C, Damaskos N J. Two-dimensional scattering by a homogeneous anisotropic rod[J]. IEEE Trans Antennas Propagat,1986, 34(10): 1243-1249.
[责任编辑:蒋海龙]
ScatteringbyaWeeklyLossyHomogeneousGyrotropicEllipticCylinder
MAO Shi-chun, WANG Fan
(Department of Basic Course Education, Suqian College, Suqian Jiangsu 223800, China)
A solution to the scattering properties by a weekly lossy homogeneous gyrotropic elliptic cylinder is obtained. The transmitted field of the gyrotropic elliptic cylinder under a transverse-electric illumination is presented. A first-order Taylor expansion is introduced to treat the Mathieu functions of complex arguments. The result is in agreement with that available as expected when the elliptic cylinder degenerates to a gyrotropic circular one.
electromagnetic scattering; elliptic cylinders; weekly lossy gyrotropic material; mathieu functions
O441
A
1671-6876(2012)03-0251-05
2012-05-15
江苏省高校自然科学基金资助项目(12KJD140004)
毛仕春 (1977-), 男, 山东日照人, 讲师, 博士, 主要从事粒子电磁及光散射研究.

