一类双圈图拉普拉斯谱刻画

刘 群

(河西学院 数学与统计学院，甘肃 张掖 734000)

一类双圈图拉普拉斯谱刻画

刘 群

(河西学院 数学与统计学院，甘肃 张掖 734000)

称图是由谱确定的，如果没有非同构的图具有相同的谱。用Cq标记长度为q的圈。圈图Cq的一个顶点与路图Pr的一个悬挂点相连，圈图Cq的一个顶点与Pr的另一个悬挂点相连，所得的图称为G(Cq，Cq，Pr)。本文将证明图 G(Cq，Cq，Pr)由它的 Laplacian谱确定。

图的谱;共谱图;特征值

0 引言

设图 G=(V(G)，E(G))是点集为 V(G)={v1，v2，v3，...，vn}，边集为 E(G)的图。本文涉及到所有图均为简单的无向图。设A(G)图G的(0，1)－邻接矩阵，dk是点vk的度数。称矩阵L(G)=D(G)－A(G)为图G的Laplacian矩阵，其中D(G)是对角元素为{d1，d2，...，dn}的n×n阶对角矩阵，记多项式P(L(G))=det(μI－L(G))为图G 的Laplacian特征多项式，I为单位矩阵。令 P(L(G))=q0μn+q1μn－1+…… +qn，其中q0，q1，...，qn是多项式的系数。因为矩阵L(G)是实对称矩阵，因此它的特征值都是实数。设μ1≥μ2≥……≥μn(=0)是图的Laplacian特征值。图G的Laplacian谱是由图G的Laplacian特征值(带重数)组成的。如果两个图具有相同的谱，那么称这两个图是共谱的很明显，如果两个图是共谱的，那么它们具有相同的点数。对于图G，如果没有非同构的图与它相关于Laplacian共谱，则称图G是由Laplacian谱确定的。

在图谱理论中，哪些图是由图谱确定的这一问题似乎是一个比较难的问题。

截止目前，只有少数图被证明有它的谱确定。本文将讨论G(Cq，Cq，Pr)的拉普拉斯谱确定问题，其中G(Cq，Cq，Pr)是指圈图Cq的一个顶点与路图Pr的一个悬挂点相连，圈图Cq的一个顶点与Pr的另一个悬挂点相连。显然它是一个具有2q－2+r个顶点和2q－1+r条边的双圈图。

1 预备知识

引理1.1［1，2］(1)设图G是一个具有n个点和m条边的图，并设d=(d1，d2，…dn)点的不增的度序列，则多项式的一些系数满足:

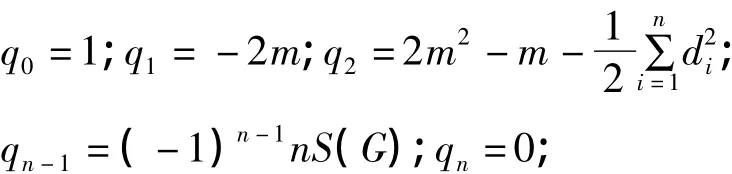
其中m是图G的边数，S(G)是图G的支撑树的数目。

(2)对于Laplacian矩阵，根据它的谱我们可以得到:

(a)图G的连通分支数;

(b)图G的生成树的数目。

(c)顶点度的平方和。

引理1.2［3，4］设图G是一个点集和边集都不为空集的图，则

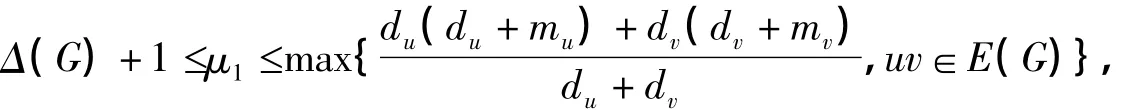
其中Δ(G)是图G中点的度数的最大值，μ1是图G的最大Laplacian特征值，mu是图G中相邻于点u的度数的平均值。

2 图G(Cq，Cq，Pr)是由它的Laplacian谱确定的

定理2.1图G(Cq，Cq，Pr)是由它的Laplacian谱确定。

证明:设图G'与图G(Cq，Cq，Pr)相关于Laplacian矩阵同谱，则根据引理2.1

和引理2.1(a)，它们有相同数目的点数、边数和连通分支数，即图G'有2q－2+r个点和2q－1+r条边，并且它是连通的，由引理2.2可得4≤μ1≤4.8，因此图G'没有度数大于3的点。设图G'中有度为i的点ni个，i=1，2，...，△'，Δ'≤3 是 G'的最大度，则

若 Δ'≤2，则 n2=2q+r，n1= －2 ＜0 矛盾，因此 Δ'=3，得 n1=0，n2=2q+r－4，因此，G'是图1 或图2:

图 1 θ(a，b，c)

图 2 G(Ct，Cs，Ph)

若 G'=θ(a，b，c)，则 a+b+c－1=2q －2+r，ab+ac+bc=q2，解得 a∈φ，b∈φ，c∈φ 矛盾。

若 G'=G(Ct，Cs，Ph)，则 ts=q2，解得 t=q=s，故 G≅G'。

定理2.2图G(Cq，Cq，Pr)是由它的Laplacian确定的。

对于一个图来说，它的Laplacian特征值确定了它的补图的Laplacian特征值，因此显然有下面的结论:

推论2.3图G(Cq，Cq，Pr)的补图是由它的Lacplacian谱确定的。

［1］ E R van Dam，W H Haemers.Which graphs are determined by their spectrum［J］.Linear Algebra Appl，2003(373):241 －272.

［2］ C S Oliveira，N M M de Abreu，S Jurkiewilz，The characteristic polynomial of the Laplacian of graphs in(a，b)-linear cases［J］.Linear Algebra Appl，2002(365):113 －121.

［3］ A K Kelmans，V M Chelnokov.A certain polynomial of a graph and graphs with an extremal number of trees［J］.Combin.Theory，Ser.B，1974(16):197－214.

［4］ J-S Li，X-D Zhang，On the Laplacian eigenvalues of a graph［J］.Linear Algebra Appl，1998(285):305 －307.

Laplacian Spectrum Characterization of a Class of Bicyclic Graphs

LIU Qun

(School of Mathematics and Statistics，Hexi University，Zhangye 734000，China)

A graph G is determined by Laplacian spectrum if there is no other non-isomorphic graph with the same Laplacian spectrum.Cqdenotes the cycle with the length of q.G(Cq，Cq，Pr)is a graph consisting of two vertex-disjoints of cycle Cqand Prjoined by a path.This paper shows that graph G(Cq，Cq，Pr)is determined by its Laplacian spectrum.

spectrum of a graph;cospectral graphs;eigenvalue

O157.5

A

1009－3907(2012)08－0989－03

2012-04-20

刘群(1979-)，女，甘肃张掖人，讲师，硕士研究生，主要从事代数图论方面的研究。

责任编辑:程艳艳