基于粒子群算法的大型风力机桨距调节计算

杨从新，吕小静，童 刚

（兰州理工大学 能源与动力工程学院，甘肃 兰州730050）

0 引 言

一般风力机风轮的气动外形是根据给定的额定风速与转速进行设计的，以保证其以最优的气动性能产生额定出力［1－2］。然而风电场的风速很少能保持为其额定值，为使风力机风轮在非额定风速下运行时还能具有尽可能高的气动性能，并且限制其过载运行，就必须使叶片安放角根据风速信号按确定方式调整，即进行桨距调节。

目前，国内的大型风力发电机组多采用统一变桨距控制技术［3］，其控制原理如图1所示。给定风速信号和功率信号，控制系统将按预先设计好的风速与桨距角的对应关系进行控制调节。

为了能够较准确地进行变桨距调节，本文将采用基于有限叶片变环量的气动模型，结合粒子群算法对大型风力机的桨距调节进行气动设计的研究。

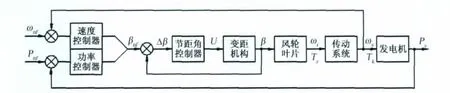
图1 桨距调节控制图Fig.1 Chart of the pitch adjusting control

1 气动计算模型的选择

风力机气动理论从Betz和Glauert建立的经典理论，到目前常用的动量－叶素理论及其修正，这些理论虽易于估算机组初始设计时整机的气动性能，但因都进行了一些假设和简化，故对叶片气动性能计算还不够准确。为了能够得到较准确的气动计算结果，本文采用一种基于有限叶片变环量的气动模型［4］。

水平轴风力机风轮的尾流可以看成是由复杂旋涡系统组成的。该旋涡系统由三部分组成：位于风轮轴线上的中心涡、沿叶片轴线的变环量附着涡以及从叶片尾缘与叶尖脱落的螺旋状自由涡层。其模型如图2所示。

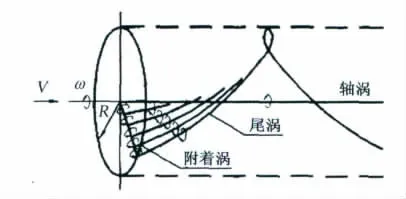
图2 风轮漩涡气动模型Fig 2 Aerodynamic vortex model of wind rotor

在上述旋涡系统的基础上，根据风力机风轮的气动计算，给出了水平轴风力机风轮的理论模型，即在不作无限叶片数与定环量假设的情况下计算叶片某断面处的旋涡诱导速度和来流下洗角，给出来流的真实速度大小和方向，用以进行风轮的气动计算。气动计算模型图如图3。

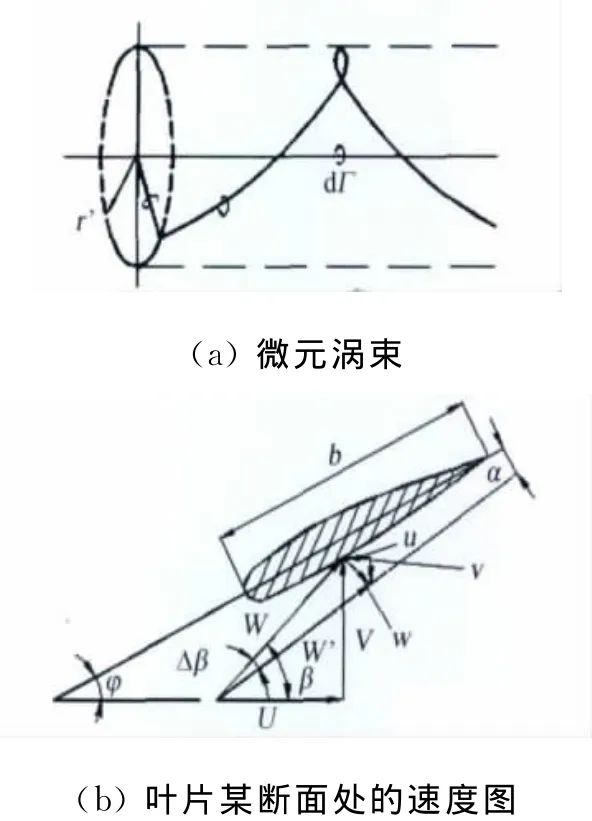
图3 计算模型图Fig.3 Calculation models

根据比奥萨法尔定理和库塔－茹可夫斯基升力公式及翼剖面理论可知，求解环量分布Γ（r）的方程如下：

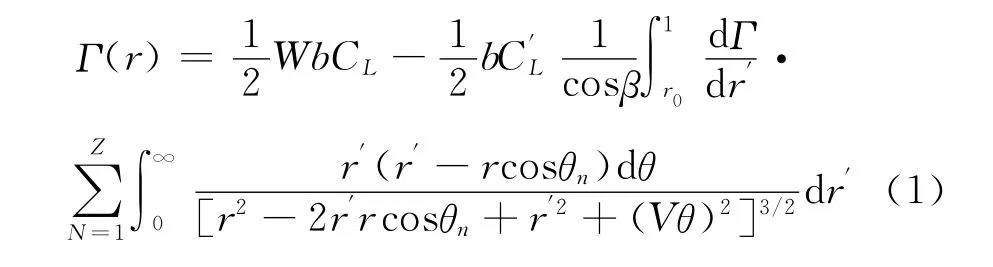
当风轮的来流条件和几何参数给定后，解此积分微分方程可得到沿桨叶分布的环量和诱导速度及下洗角。进而求得推力系数CF和功率系数CP，其无因次量形式的表达式为 ：

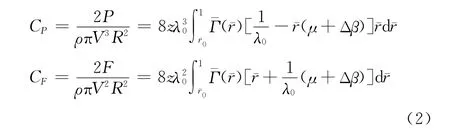
式（1）中CL为升力系数，C′L为升力系数对攻角的导数，θn＝θl＋2π（n－1）／z，θ为中心角，n为叶片断面数。式（2）中P为功率，F为轴向力，z为叶片数，λ0为叶尖速比，μ为翼型升阻比的倒数。各式中其它参数如图2和图3所示［4－7］，均为叶片任意断面位置r的函数，符号上方带横线的各参数为其无因次量。

2 粒子群算法简介

粒子群优化（Particle Swarm Optimization，PSO）算法是近年来发展起来的一种新的进化算法。该算法将从初始化的随机解出发不断迭代更新，最终找到最优解。迭代中粒子根据如下两个公式来更新自己的速度和新的位置：

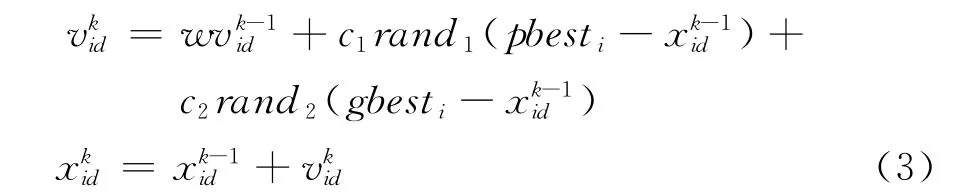
式（3）中i＝1，2，...，m；d＝1，2，...，n；m为粒子的个数；n是解向量的维数。vi是粒子的速度，xi是粒子的位置。pbest和gbest分别是个体极值和全局极值，c1和c2通常等于2，rand1和rand2是两个独立的介于［0，1］之间的随机数；w是动量项系数，调整其大小可以改变搜索能力的强弱，本文取0.75［8］。

本文以水平轴风力机为研究对象，优化设计编程方框图如图4所示。

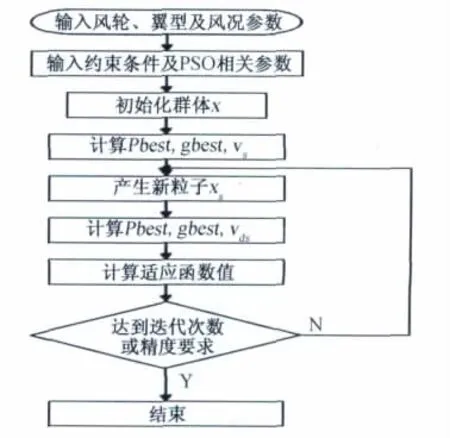
图4 粒子群算法流程图Fig.4 Flow chart of PSO program

3 风力机桨距气动设计的PSO实现

文中采用风力机专用翼型S809，以设计一1.5MW的恒速变桨风力机为例进行优化设计。该风力机的主要气动与几何参数为：直径D＝70m，额定风速V0＝12m／s，切入风速Vin＝3m／s，切出风速Vout＝25m／s，额定转速n＝18.8rpm，额定功率W＝1500kW，叶片数z＝3。叶片几何外形设计结果如表1所示。

3.1 桨距气动的优化分析

对于大型恒速变桨风力机组，当风速低于额定风速时，应使风轮的桨距角向负方向调节，来维持最佳攻角，以提高风能利用系数。即V＜V0时，以各个风速下需调节的变桨角为搜索变量，目标函数为：f1（Δφ）＝CP（Δφ，V），给出变桨角 Δφ的约束范围：φmin＜Δφ＜φmax搜索使f1（Δφ）达到最大值时的值，即得到各个风速下调桨距的角度。

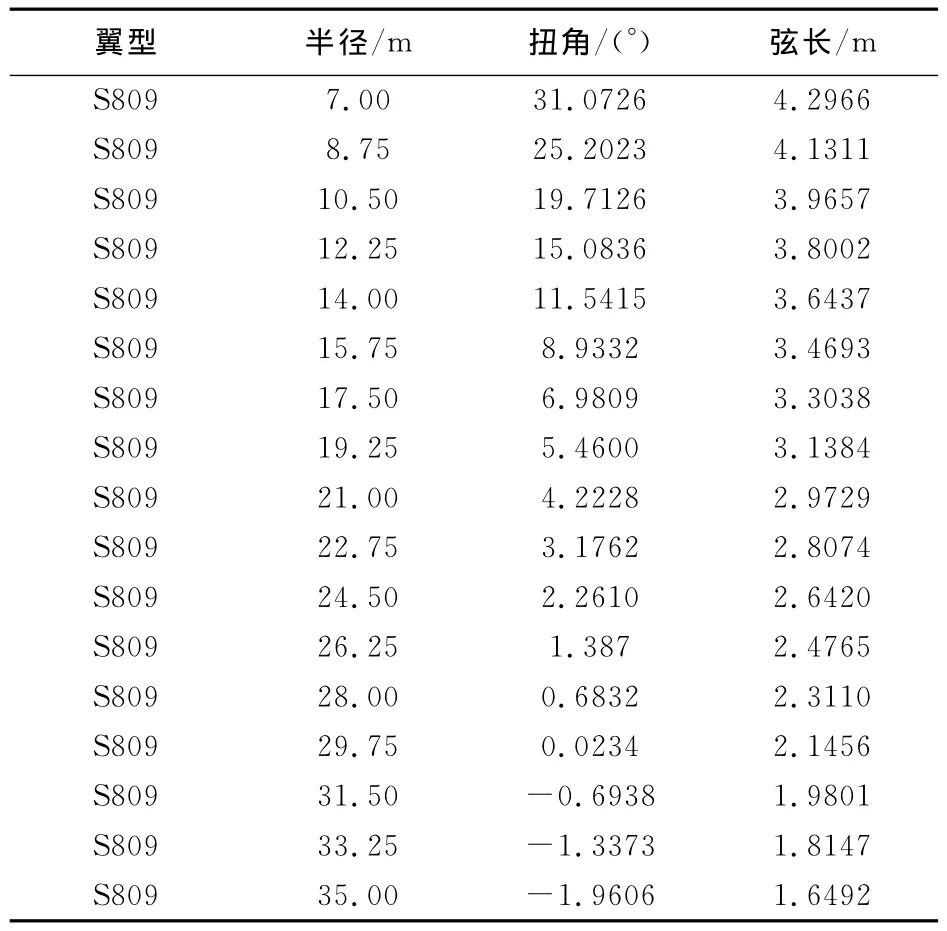
表1 优化设计结果Table 1 The results of optimal design

当风速高于额定风速时，应使风轮的桨距角向正方向调节，攻角变小，减小风能利用系数来保证额定功率的输出。即V＞V0时，求出各欲设计风速下应满足的各个CP值，使其作为目标向量，各风速下应满足的变桨角作为搜索变量，目标函数为两个向量差的模：f2（Δφ）＝｜CP（Δφ，V）－CP｜给出变桨角 Δφ的约束范围：φmin＜Δφ＜φmax搜索使f2（Δφ）达到最小值零时的Δφ值，即得到各风速下调桨距的角度。

风轮经桨距调节后，所改变的只是其各径向位置处的叶片安放角。根据调桨后安放角的更新和原额定的叶片气动与几何参数（直径，弦长，翼型及其气动性能系数），即可计算风轮在各风速下的气动性能。

3.2 优化设计结果

根据PSO流程图，搜索出Δφ，各风速下桨距调节值如图5所示。优化设计出的桨距调节值变化曲线呈线性分布，易于调节，这和现行桨距角调节理论相吻合。

根据桨距调节公式φ（v）＝φ（v0）±Δφ（v），结合额定的叶片气动与几何参数，即可计算风轮在各风速下的气动性能：风能利用系数CP（V），轴向力系数CF（V），出力的转速特性P（V），及轴向力的转速特性F（V）。

各风速下桨矩调节设计计算结果及气动性能曲线分别如表2和图6－7所示。

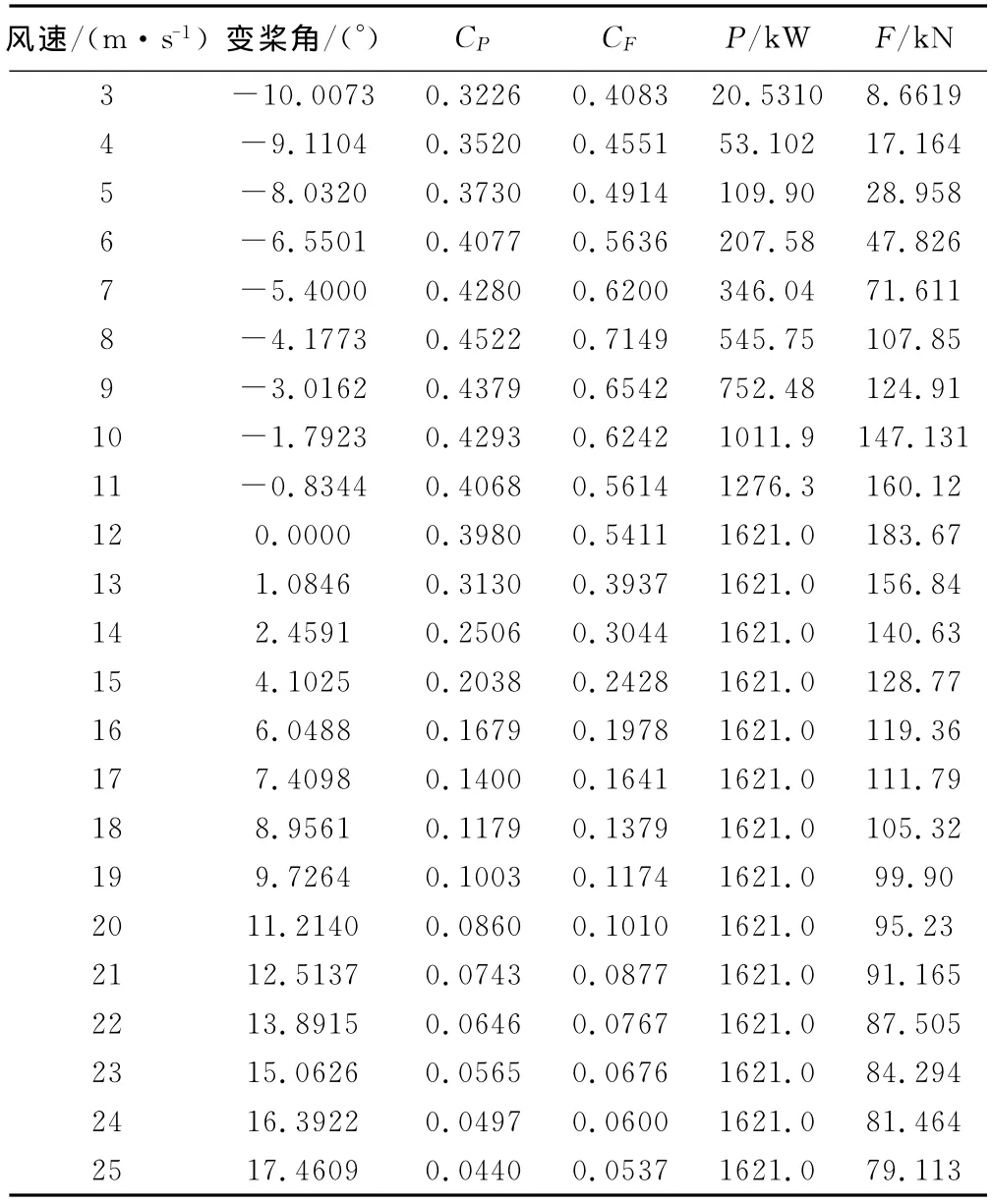
表2 桨矩调节设计计算结果Table 2 The design results of the pitch regulation

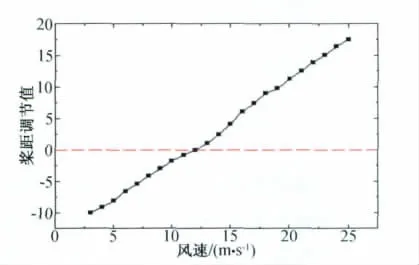
图5 桨距调节曲线Fig.5 The pitch regulation curve

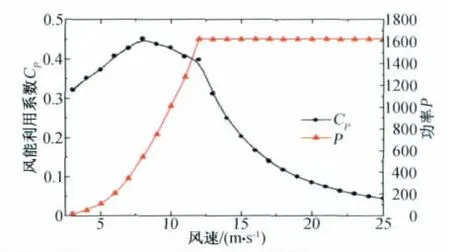
图6 功率系数和功率曲线Fig.6 Power coefficient and power curves

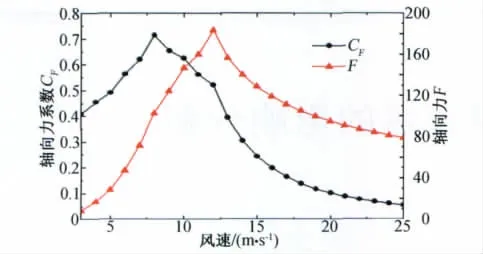
图7 轴向力系数和轴向力曲线Fig.7 The axial force coefficient and axial force curves

3.3 结果分析

（1）从气动外形优化设计的结果（见表1）可以看出，基于有限叶片变环量的气动模型与粒子群算法相结合的优化设计计算方法设计出的风力机叶片，其安放角和弦长沿叶片展向分别按贝塞尔曲线和线性进行分布，这与同类型同功率风力机沿叶片展向所设计的安放角和弦长分布情况趋势一致，说明了本文的优化设计计算方法是可行的。

（2）从桨距气动优化设计的结果（见图5）可以看出，当风速小于额定风速12m／s时，桨距角需往负方向调节；当风速大于额定风速12m／s时，桨距角需往正方向调节，这与桨距角调节理论相吻合。

（3）从桨距气动优化设计的计算结果（见图6、图7）可以看出，计算出的CP（V）、CF（V）在风速等于8m／s时达到最大值，随着风速的逐渐增大其值逐渐减小；功率P和轴向力F从切入风速到额定风速呈上升趋势，从额定风速到切出风速，由于对桨距进行调节功率P保持不变，轴向力F逐渐减小。这与现行风力机桨距调节的气动性能曲线变化一致。从而进一步说明本设计计算方法的可行性。

4 结 论

（1）本文采用基于有限叶片变环量的气动模型，结合粒子群算法对大型风力机桨距调节进行了气动优化设计和计算，优化设计计算出的特性变化趋势与实际风力机运行相符，证明了该设计计算方法的可行性和有效性。

（2）为保证设计结果为全局最优解，并加快搜索的速度，文中采用了粒子群算法，这种方法在风力机气动优化过程中，可以更快收敛于最优解，保证了解的质量。

［1］GOURIERES D L.Wind power plants：theory and design［M］.NewYork：Pergamon Press，1982.

［2］贺德馨.风工程与工业空气动力学［M］.北京：国防工业出版社，2006.

［3］叶杭冶.风力风电机组的控制技术［M］.北京：机械工业出版社，2002.

［4］CHENG Z X，YE Z Q，CHEN J Y，et al.Aerodynamic optimization for the rotor of horizontal－axis wind machine［A］.Proceedings of the International Conference on New and Renewable Energy［C］.Beijing，1990.

［5］BURTON T，SHARPE D，JENKINS N，et al.Wind energy handbook［M］.Chichester：John Wiley ＆ Sons，Ltd，2001.

［6］SPERA D A，et al.Wind turbine technology：fundamental concepts of wind turbine engineering［M］.New York：ASME Press 1994.

［7］KRAMER R，ARCHER R.Modelling approaches for flow over a wind turbine blade［J］.WindEngineering，2004，28（3）：311－323.

［8］汪定伟，王俊伟，王洪峰.智能优化方法［M］.北京：高等教育出版社，2006.