微分雷诺应力模型在激波分离流中的应用
聂胜阳,高正红,黄江涛
(西北工业大学 翼型叶栅空气动力国防科技重点实验室,陕西 西安710072)
0 引 言
基于Boussinesq涡粘性假设的湍流模型在很多工程流动类型上有很好的预测能力,但是对一些特殊的流动,它会给出与实验较大的差别。平均应变率的突变导致这些湍流模型失效并不奇怪,雷诺应力的相应变化是与自由来流进程和时间尺度不相关的变化率衡量,所以导致Boussinesq涡粘性假设失效。同样,当流动中因快速膨胀,剧烈变形,或者大的流线弯曲产生的额外应变率,都会产生不平衡的法向雷诺应力,涡粘性假设就失效了。
为了修正这些问题,在涡粘性模型的基础上加入曲率修正[1],应用于存在大的流线弯曲的情形如旋涡流动。另外一种更近似描述雷诺应力张量而不引入附加方程的方法是假定Boussinesq近似是雷诺应力级数展开项的主导项,这样流动中引入各向异性的雷诺应力分量,这就是代数应力模型(ASM)。这种模型在流体各向异性特性显著的流动中,预测较好,但它还是基于两方程的涡粘性假设的模型,和它们的缺点一样[2]。
本文将完全雷诺应力方程的模式化过程进行了详细阐述,应用一系列模式将其封闭,得到微分雷诺应力模型(DRSM);将其与广泛使用的几种湍流模型应用于较大攻角的跨声速ONERA M6机翼的计算,表明其在激波分离流动中具有更好的预测能力;对各种模型的不足之处进行了讨论,为模型的改进工作提供参考。
1 不可压雷诺应力方程
雷诺应力的差分方程完整地描述了雷诺应力张量,τij≡-,其不可压的形式为:

其中:

称为扩散项;由式(1)可以看出,第一,方程中已经包含了τij的对流和扩散,所以二阶矩模型包含流动发展历程的影响。耗散项和湍流输运项中的时间尺度是和平均流动时间尺度不相关的,所以二阶矩模型的上游历程的影响要比两方程湍流模型中人为添加的上游历程的影响更真实;第二,式(1)包含了对流项、产生项和体积力项,这些项对流线弯曲,流体旋转等起主要作用。所以二阶矩模型如果模化的好,也能更真实地包含这些产生不平衡雷诺应力的作用;第三,式(1)并没有反应出法向应力相等,即使平均应变率为0,也就是说,它的值由初始条件和流动进程决定。因此,二阶矩模型能够处理平均应变率有突变的情况。
2 模式假设
为了封闭方程(1),必须对耗散项张量,再分布项张量,扩散项张量进行模化。耗散项:
因为耗散作用发生在最小尺度的涡,因此耗散项的建模就相对简单,大家都采用Kolmogorov(1941)提出的当地各向同性假设,即:

这里

标量ε就是湍动能方程中的耗散率。而对耗散率的建模可参考k-ε两方程模型中的耗散率方程的处理方法。
由于实际中的耗散率是各向异性的,尤其是靠近壁面处,所以为引入这一特性,后人进一步修正耗散项为:
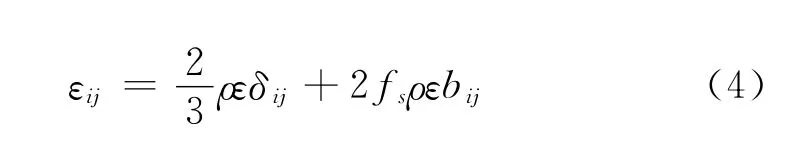
其中bij为无量纲化的雷诺应力各向异性张量,即
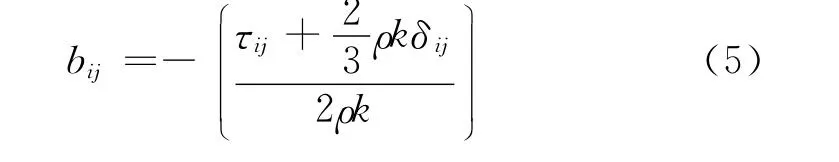
fs是经验性的添加的衰减函数,为

ReT为定义的湍流雷诺数,为

扩散项:
扩散项中包含压力脉动项和三阶速度脉动项,表示脉动压力和雷诺应力对能量的输运作用。现有的实验数据无法找到有用的信息去模型化压力脉动关联项。最简单而又常见的模化扩散项的方法是假定一个梯度输运进程,并且引入分子粘性作用。这里使用Launder,Reece和 Rodi(1975)[2]提出来的一种近似方法:

这里他们建议Cs≈0.11。这也是涡粘性假设的湍流模型处理扩散项常用的方法。再分布项:
压力张量再分布项也叫压力张量关联项,是最难模式化的部分。第一,它和产生项是同阶的;第二,它包含大量不可测的关联项,模式假设缺乏足够的理论依据及实验数据。再分布项有两种主流的模型化方法,分别是Launder,Reece和 Rodi(1975)等提出的LRR压应力模型以及Speziale,Sarkar和Gatski(1991)等提出的SSG压应力模型,具体参考文献[3]。本文选取较简单的SSG模型来模化:

这里bij定义如式(5)。
Speziale,Sarkar和Gatski给出的模式参数为:

Willin &Johansson[4]给出了一组较简单的模式参数为:

3 可实现的DRSM
3.1 引入压缩性修正
可压流动的特征是密度的显著变化。在马赫数小于5(另一说为8)时[2],壁面流动受压缩性影响很小,因为通过激波,在小距离内压力梯度变化不剧烈。Tw/Te在边界层内压缩性对涡的作用也不明显。基于这样的事实,Morkovin(1962)认为湍流的密度脉动量相对与自由来流是个微量,因此在湍流模式中使用不可压的形式[2]。但 Morkovin假设在即使不是高超音速情形下也有其局限性,因为密度脉动量相对自由来流的密度并不是小量。所以压缩性效应明显的流动情形,应将密度脉动量考虑进去,一种有效的数学处理方法就是采用Favre(1965)的质量平均速度的概念,定义为:

某时刻瞬时速度为:

这样在湍流模型中也就反映了密度的脉动。这里直接给出Favre平均的雷诺应力方程,具体推导过程见参考文献[2]:

其中:
产生项:Pij=-
再分布项:Πij=
耗散项:εij=
扩散项:Dij=-
压力作用项:PWw=
对比可压和不可压的完全雷诺应力方程,可以发现,方程多了压力作用项,这个由压缩性引起的项在不可压流动中是零。其他项的物理意义与不可压方程相同,但在形式上由于引入质量平均概念而有所不同,对再分布项,耗散项和扩散项的建模思路和不可压的二阶矩模型一样,自由来流的速度项均需采用式(12)中定义的质量平均速度。
由于压力作用项是脉动量和平均量的耦合,还没有合适的模型去表征它的特点,并且单个脉动量在时间平均中是可以忽略掉的,本文去掉压力作用项。
3.2 耗散项εij的改进
前面介绍二阶矩的模型化过程,但没有给出耗散率ε的方程。这是因为,在壁面上,耗散率为ε=0,所以在壁面上,式(1.7)、(1.8)中均出现奇点。在计算中,ε会在壁面附近剧烈变化,因此在壁面附近需将网格划分的足够的小。因此本文采用Wilcox(1988)等[5]提出的比耗散率ω的输运方程来模化耗散项。输运方程为:

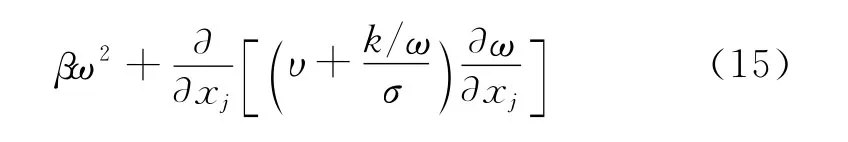
模式参数为:

耗散率补充方程为:

由前述的式子就将SSG-ε模型发展成了SSG-ω模型。
4 模型验证
选用ONERA M6机翼,计算状态为Ma=0.84,α=6.06,Re=11.7×106。这是一个跨音速大迎角状态,实验数据来自参考文献[6]。
本文计算采用的离散格式为中心格式添加适当的人工粘性,对时间推进采用显式三步Runge-Kutta推进。采用多重网格和隐式残差光顺等措施加速收敛。计算网格为非结构网格,粘性层用25层三棱柱,第一层的高度为1e-6,外推比例为1.3。为了对不同湍流模型计算效果进行比较,计算过程采用同一套分布合理的网格,使用相同的时间推进手段和CFL数,自由来流的湍流度和湍流粘性比相同。
图1和图2给出了表面极限流线计算结果,可以看出M6机翼在该状态时,出现 形激波,在翼展60%处,激波汇合,形成更强的激波,波后由于强的逆压梯度,出现大范围的分离涡。比较发现,SA模型和SST模型的分离区域最大,在机翼中段激波后就出现了轻度分离。汇合后的激波靠近前缘,尤其是SA模型。SST模型预测出来的激波不平直。而基于Wilcox提出的标准k-ω两方程,以及基于标准k-ω两方程的SSG-ω模型和Willin &Johansson提出的改进SSG-ω模型预测出相似的极限流线分布和激波形状和位置,W&J改进的SSG-ω模型预测出的分离区域,流线更紊乱,标准k-ω模型预测出的激波位置更靠近下游,激波后的流动更光顺。
从压力分布与实验数据的对比上,80%展向位置之前,SST模型给出最接近实验的激波位置,但波后的分离较大,整个后半区域都是低压区;在80%展向外,SA和SST模型对大的分离流动和激波位置预测失真,而基于SSG压力关联项假设的DRSM预测的激波位置最接近实验,波后的分离流动虽然不是很贴合,但也可以接受。而 Wilcox的标准k-ω模型给出的激波位置靠后。

图1 计算网格、表面压力系数分布和表面极限流线图(SA、SST、k-ω、SSG+ω和W&J SSG+ω)Fig.1 Surface and symmetry grid &surface pressure coefficient distributions &surface skin friction lines(SA、SST、k-ω、SSG+ω & W&J SSG+ω)

图2 等压线分布图Fig.2 Iso-surface pressure coefficient lines distributions

图3 各站位压力分布对比Fig.3 Pressure coefficient distributions at different standings
SA和SST都过度地预测了激波后的分离流动,这可能是在这种出现强的激波附面层干扰和强逆压梯度时,两种模型都没有很好地限制空间湍流粘性系数的非物理性增加,而基于k-ω模型的计算在激波位置的预测上显得滞后,这与附面层内湍流粘性系数的过度增长有关,但在激波后,又很好地限制了这种增长。而DRSM模型直接对雷诺应力分量建模,在各向同性流体中就退化成了Wilcox标准k-ω模型。
可以总结出,DRSM模型较一方程和两方程模型,如本文第一部分所述,对快速膨胀,流线弯曲等流体各向异性性质显著的流动预测更加合理。Willin&Johanson的改进参数在激波位置的预测上稍好,但改进余地有限。
在流线比较规则的区域,压力梯度比较和缓,如机翼80%展向之前,SA模型和Menter的SST模型对激波位置的预测比本文使用的其他湍流模型更好,尤其是SST模型。单独比较Menter的SST模型和Wilcox的标准k-ω模型,SST模型是在近壁处采用Wilcox的标准k-ω模型,在边界层边缘和自由剪切层采用k-ε模型(k-ω形式),其间通过一个混合函数过渡。这就是Menter的BSL模型改善对自由来流ω值的敏感性的思路。其应用表现和Wilcox的标准k-ω模型类似。故通过修改ω的输运方程达到改进DRSM的目的是不可行的。数学上分析两方程模型在有逆压梯度流动中的表现很大程度上被限定在对数区。尽管模型在对数区的模拟能力很重要,尤其是有强的逆压梯度,但尾流区的涡粘性系数却决定了涡粘性模型对强逆压梯度的预测能力。为此Menter参照Johanson &King模型,考虑了湍流剪切应力的输运而修改了涡粘性的表达式,使模型对强逆压梯度流动的预测更加合理(具体见参考文献[7]),对太强的逆压梯度分离的预测又显得太敏感。而标准的kω模型不能准确预测压力诱导的分离,使得激波位置靠后,而又限制了分离的发展。完全雷诺应力模型,也就是二阶矩模型考虑了湍流剪切应力的输运,理论上说能预测压力诱导的分离流动,但计算结果表明DRSM较两方程的标准k-ω模型只是在激波位置上较好,这让人不由得想到在对二阶矩模型压力再分布项模化的时候使用的SSG模型。SSG压应力模型较LRR压应力模型简单,它不需要LRR模型那样,为获得较好的对数层的解,而加壁面反射作用修正,这也许就是在强逆压梯度区SSG模型未能较好地预测出激波位置的原因。因此,更为合理的微分雷诺应力模型应当综合SSG模型的简洁性和LRR模型的准确性,在边界层内使用LRR-ω模型,在边界层外使用SSG-ε模型,通过类似与Menter的BSL模型中的混合函数来过渡。
5 结 论
涡粘性假设和代数应力模型都是基于雷诺应力方程而简化建立的模式假设。雷诺应力方程是对雷诺平均假设下最完整的描述湍流的控制方程,因此本文着眼于直接对雷诺应力方程的建模,也就是利用微分雷诺应力模型求解激波分离流这种复杂的流动;由于雷诺应力方程引入了22个未知量,需大量合理的模式假设将其封闭。本文总结前人工作的基础上,应用成熟的一系列假设将雷诺应力方程封闭,并针对本文应用的流场特点,引入了压缩性修正和改进的耗散率方程,构造出可实现的微分雷诺应力模型(DRSM);将此模型和传统的一方程模型(SA)和两方程模型(SST、Wilcox标准k-ω)应用于较大攻角的跨音速ONERA M6机翼的计算,结果表明,SA和SST在流场未出现大的分离前能较好地预测激波位置但分离程度都过大,出现激波诱导的大分离后分离流态和激波位置都严重失真,而DRSM在激波诱导的分离区域表现较好。
[1]SPALART P R,SHUR M L.On the sensitization of turbulence models to rotation and curvature[J].AerospaceScienceandTechnology,1997,1(5):297-302.
[2]WILCOX D C.Turbulence modeling for CFD[R].DCW Industries,Inc.1994.
[3]SPEZIALE C G,Sarkar S,Gatski T G.Modelling the pressure-strain correlation of turbulence[J].Fluid Mech,1991,227:245-272.
[4]WALLIN S,JOHANSSON A.An explicit algebraic Reynolds stress model for incompressible and compressible flows[J].FluidMech,2000,403:89-132.
[5]WILCOX D C.Reassessment of the scale determining equation for advanced turbulence models[J].AIAA Journal,1988,26(11):1299-1310.
[6]SCHMITT V,CHARPIN F.Pressure distributions on the ONERA-M6-wing at transonic Mach numbers[R].AGARD-AR-138.May,1978.
[7]MENTER F R.Two-equation eddy-viscosity turbulence models for engineering applications[J].AIAAJournal,1994,32(8):1598-1605.

