细长杆降低超声速客机气动噪声的数值分析
沈 沉,周 华
(同济大学 航空航天与力学学院,上海200092)
0 引 言
超声速客机在飞行速度方面的优势使其自诞生之日起就受到世界的瞩目,但是由于经济性较差、飞行噪声过大,使这种飞机的发展一波三折,唯一实现航线飞行的是由英法联合研制的“协和”式飞机。“协和”式飞机靠英法政府补贴弥补其经济性较差的缺点,同时为了避免噪声带来的环境问题,“协和”式飞机的航线被设计到大西洋上空。2003年,在一次机毁人亡的严重事故后,“协和”式飞机正式退出运营。但是超声速客机的研究一直没有停止,美国和欧洲都有相关的研究计划,甚至还包括研制高超声速客机的设想。为了解决超声速客机带来的噪声问题,欧美都有相关的研究项目,希望克服经济性和飞行噪声问题。这两个问题的解决无疑将扫清超声速客机进入商业运营道路上的技术障碍。
超声速客机的飞行噪声主要来源于超声速飞行时产生的“音爆”现象。超声速空气动力学告诉我们,飞机以超声速飞行时,它在远场对空气的扰动与细长旋成体等价,其流动特征由头部激波、膨胀波和尾部激波决定,其压强分布形成典型的字母N的形状,因而常被称为“N波”。“N波”扫过地面时,地面上的居民可以听到类似雷声滚过的轰鸣,这就是所谓“音爆”现象。为了减弱“音爆”带来的噪声问题,各国研究人员提出各种技术手段用于降低气动噪声,包括使用航迹优化和改变气动外形两大类方法。航迹优化包括将航线设计到无人区上空并增加起飞着陆时的飞行角度以减小受影响的区域。改变气动外形的方法则是试图通过减小客机尺寸、改变客机气动外形和加装降噪装置三种途径实现降低飞行器对空气的扰动,改变激波形状和强度,进而达到减弱"音爆"的目的。本文研究的降噪手段属于后者,意图在于用加装在飞机头部的细长杆改变头部激波形状,进而减弱“音爆”的影响。
细长杆降噪方法的设想最早诞生于20世纪60年代,它既有空气阻力相对较小的优点,还对机体改动小。通过分析比较各种细长杆的降噪效果,本文经过研究分析获得细长杆降噪性能的一系列初步结论,这些结论可供超声速客机设计人员参考。
如前所述,超声速客机的噪音主要源于音爆,而对音爆的分析一般分为近场、中场和远场。客机以超声速飞行时在空气中产生扰动,扰动通过大气传播至地面的过程基本是轴对称型的。气体静压曲线的特征形状在传播过程中演变,气体的各个参数在大尺度范围内仍具有明显的非线性效果。由于满足几何声学方程,飞机产生的音爆会在大气传播过程中收敛叠加,在远场形成了静压特征曲线相对固定的“N波”。假设波幅衰减因子在大气中恒定,根据特征线的观点[1],过压δp只与音爆传播距离有关。超声速飞机产生噪声的实质是激波在大气中传播,在远场仍能产生较大的压强差,从而产生音爆,因而,研究降噪的本质办法要从控制激波入手。
传统的音爆计算方法采用诸如 TRAPS[2]、ZEPHYRUS[3]、PCBoom3[4]等音爆程序计算远场音爆,然后结合CFD计算得到的近场解来使两者相互适应。这种方法的计算量较小,但由于采用不同数值方法分别求解近、远场,难以具有很好的说服力。由于计算机性能的不断提高,使本文采用统一的CFD算法求解近场与远场成为可能。本文综合考虑计算成本和计算精度,采用自适应网格,以使求解更加快速、精确。下面通过对比实验数据以及传统音爆理论,以说明数值算法的准确性。
1 数值模型及其验证
为了检验本文所用的数值模型,本文将计算结果与湾流公司的飞行试验数据进行对比,以此验证数值模拟结果的可信度,为后续工作打下基础。
Preston等人提出的细长杆降噪小型超声速民航机方案如图1所示[5]。本文将此民航机作为数值可信度分析参照物,使用由此型号导出的的外形尺寸参数进行计算,以便于与试验结果进行对比。由于我们只关心飞行噪音对地面的影响,因此将此飞机简化为细长旋成体(如图2),便可以将与其音爆相关的流场计算转化为准三维问题求解,从而大大缩短计算时间。

图1 湾流公司细长杆降噪小型超声速民航机方案Fig.1 Small supersonic civil aircraft of Gulfstream
图2 机身准三维简化结构Fig.2 Simplified structure of quasi-three-dimensional body
下面算例中的飞行马赫数为1.6。划分网格时首先用马赫角来预估激波范围,确定计算域。然后对此计算域用四边形网格划分,原始网格数量15万。在计算过程中,以压强梯度为变量,应用自适应网格方法处理网格,在激波附近加密网格,然后重复计算。求解中采用了密度基定常求解器耦合能量方程的方法求解全场,大气采用粘度满足Sutherland关系的理想气体模型模拟,使用Spalart-Allmaras湍流模型以及压力远场边界条件,以隐式格式进行计算。本文采用的预分裂法能克服矢通量分裂格式精度不足和通量差分裂格式计算量较大的缺点,符合本文的带细长杆超声速客机的数值模拟精确高效的要求[6]。
本文通过逐步增加网格数量的方式(图3、图4),观察网格数量对计算结果的影响,验证网格无关性检验。结果证明,在本文计算中,当网格密度增加到40万以后,可以达到网格无关性的要求。

图3 飞机附近的计算域原始网格Fig.3 Original mesh around the aircraft

图4 自适应处理后激波路径上的网格Fig.4 Self-adapted grid along the shock path
调用近场数据,画出静压分布曲线(图5)并与实验曲线(图6)对比,可见两条曲线的走势基本一致,曲线前段也有锯齿状上升,两者在前半段基本吻合。明显的不同处体现在两个方面:(1)尾部压强曲线出现突起;(2)模拟结果中的静压最小值低于实验结果中的值。
这两方面的误差是由于实际模型机身后半段与准三维轴对称体差异较大。实际民航机由于垂尾的存在,使得机尾激波较弱且偏转角大无法顺利扫到地面所以不存在尾部波形突起,而数值模拟的尾部激波比较强会引起特征波形在这点的压强骤增;而且实际民航机后段机腹纵截线曲率半径较大,产生的膨胀波系较弱,不能像轴对称模型那样明显地降低地面压强,导致了数值模拟数据与试验数据的压强最小值差异。虽然后半部分用准三维模型模拟存在一些误差,但考虑到细长杆是安装在机头部位,属于机身前段,用数值模拟方法比较各种细长杆降噪效果的结论也具有可信性。
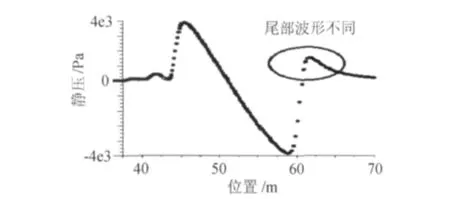
图5 数值模拟静压曲线Fig.5 Static pressure curve of numerical simulation
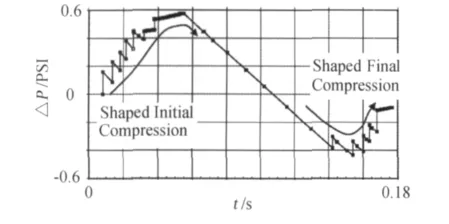
图6 湾流公司实验曲线Fig.6 Experimental static pressure curve of Gulfstream
将各个距离静压峰值用连线表示(图7),从模拟结果中我们可以看到距飞行轨迹不同距离位置的静压情况是满足细长体近场压强场的基础理论公式[7],静压峰值与半径的四分之三次方成反比,说明在这一点上数值模拟结果是与理论相符合的。根据前文的论述,超声速飞机在远场会产生“N波”,而将“N波”理论结果[8]叠加到650m处的数值模拟结果上对比(图8),发现两者走势基本吻合。由此可见,通过与已有实验数据和音爆理论的对比,表明上述用于模拟音爆的数值方法是合理有效的。

图7 飞行轨迹上不同站位的压强变化Fig.7 Pressure variation at different stations on the flight path
2 设计方案与计算结果
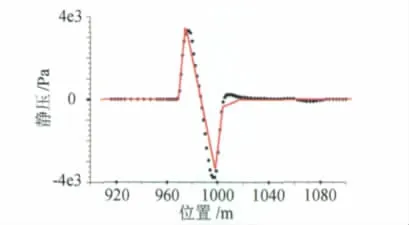
图8 理论波形在数值模拟结果上的对比Fig.8 Comparison between the numerical simulation results and N-wave theory
超声速客机头部激波形状在大尺度范围看主要由飞行马赫数决定,而根据锥形流理论,头部激波形状在近场小尺度范围内则由头锥的锥角和飞行马赫数共同决定。细长杆降噪的主要机理就在于用细长杆改变头部激波近场形状,进而改变头部激波强度,减弱“音爆”形成的噪声水平。从另外的角度看,加装细长杆后,超声速客机的长细比增加,这意味着激波阻力下降,而激波阻力下降的根本原因是激波强度减弱,显然有助于减弱“音爆”带来的噪音。
基于对上述基本机理的认识,本文设计了6组细长杆方案,包括双锥体方案、台阶体方案、钝头体方案、连续压缩体方案、流线型细长杆方案和整体锥形细长体方案,加上作为对比参照物的无细长杆方案,共计算了7组13种方案(表1):
a)三种双锥体细长杆方案用来确定双锥体细长杆降噪效果与锥顶角的关系。
b)两种台阶体细长杆模型是受美国SSBD验证项目中F-15B战机实验的启发,希望找到台阶数对降噪的影响。
c)钝头体细长杆能在钝头前方拉出一道弓形脱体激波,而弓形激波的激波较强,可能有较好的降噪效果,这里做尝试分析。
d)连续压缩细长杆方案是本文独创的,这种方案的特点是细长杆前部由连续的凹面构成,超声速气流在凹面上产生连续的压缩波,而不是孤立的贴体激波。提出连续压缩方案是因为对来流进行连续压缩可以产生较弱的脱体激波,可能有较好的降噪作用。与凹面相连接的曲面包括锥面、一阶连续凸面和凹面三种型式,目的在于考查各种后向曲面产生的膨胀波与前方连续压缩形成的激波之间的相互干扰关系,同时考察衔接两个曲面的锐边对噪声的有什么影响。
e)流线型细长杆模型也是本文独创的,虽然前部有较大的锥角,后段则有较大范围的膨胀波区域可能对细长杆顶端的激波有一定的干涉作用。
f)整体锥形体的锥角明显小于飞机头锥的锥角,根据锥形流理论,由此产生的一道斜激波的强度将小于头锥产生的激波强度。设计这个方案就是要验证局部较小的激波锥角对远场激波锥角的影响。
为了在模拟中计入机身影响,同时为了简化计算,本文以“协和”式客机的几何构型为基准,设计了细长旋成体代替机身的作用。各种方案中的细长杆在计算中直接加装在细长旋成体上,细长杆长度统一为8m。采用细长旋成体机身后,可以用准三维模型进行分析。使用第3部分的计算方法,采用相同的湍流模型和步骤,将马赫数修改为2,其他参数不变,迭代至收敛后使用自适应网格以提高精度,并验证网格无关性。
从等高图、坐标表示(图9)、列表(表2)三个方面对距飞行轨迹50m和1200m处的计算数据进行后处理,观察远场N波、激波强度、激波倾角。

表1 各种细长杆方案Table 1 Various slender-rod designs
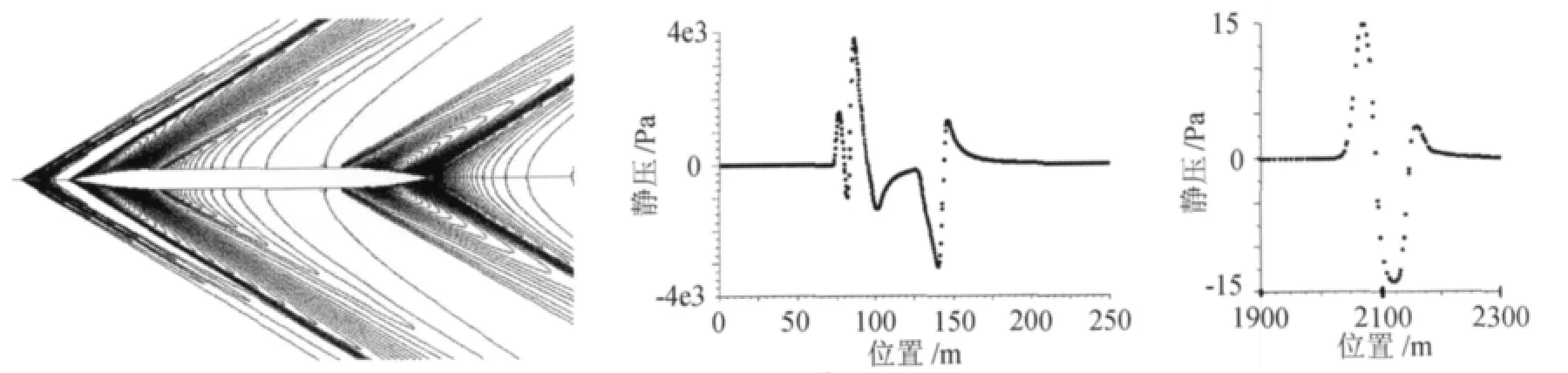
图9 典型的近场等高线图、典型近场静压曲线、典型远场“N波”曲线Fig.9 Typical near-field contour,typical near-field static pressure curve,typical far-field N-wave curve
这里采用声压级参数来量化比较的降噪效果。由于噪声的实质是空气中的压力脉动,且各类细长杆方案的机头激发的激波所形成的压力阶跃脉宽相近,因此可以直接利用远场最大静压的声压级降低值来衡量。降噪效果声压级应满足下式:
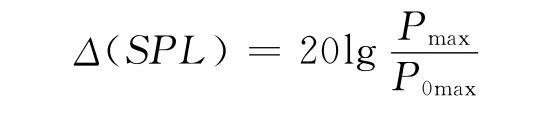
其中Pmax为细长杆方案的远场静压最大值,P0max为无细长杆方案的远场静压最大值。列表比较声压和较降噪分贝数。
本文从表2数据得出以下规律:
a)双锥体细长杆顶角越小,远场的噪声水平越低,降噪效果越好。
b)台阶数越多,远场噪声水平越低,降噪能力越好。
c)外形光滑(一阶连续)的细长杆降噪效果比带锐边的细长杆好,平滑过渡(一阶连续)的细长杆形状具有更低的N波峰值。
d)各种方案的降噪效果优劣:5°锥顶角方案降噪效果最好,连续压缩降噪效果较好,多台阶也具有降噪效果,前凸方案降噪效果不明显,其他方案没有降噪效果。
e)细长杆形状对局部激波倾角有影响,但对大尺度的远场激波倾角影响不大。
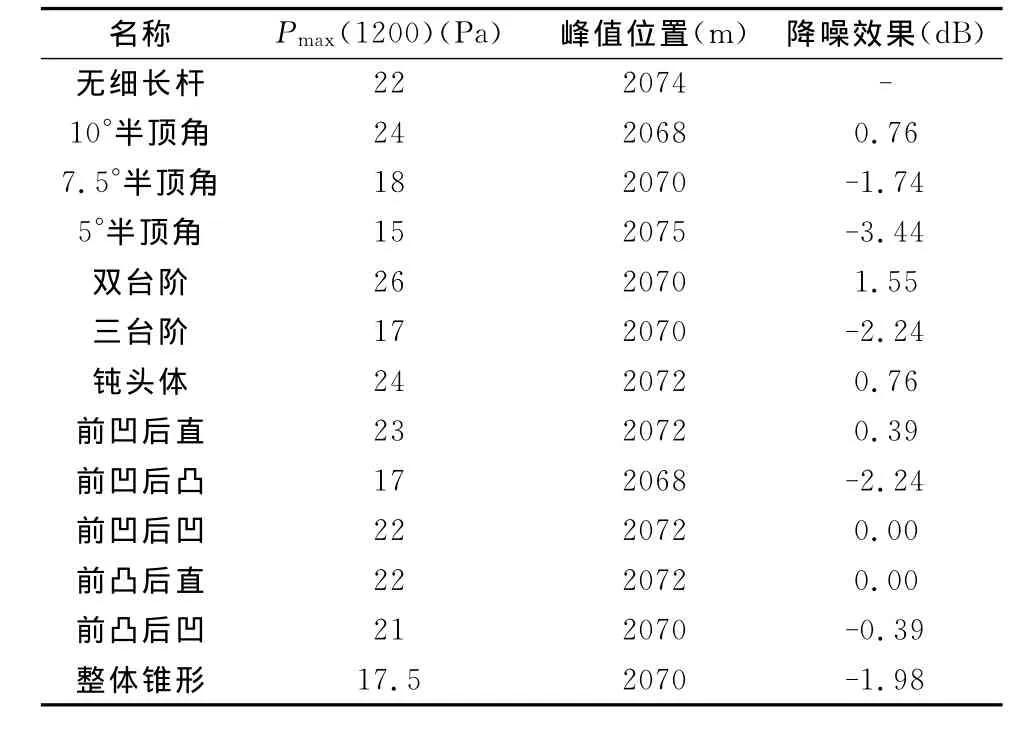
表2 各种细长杆模型远场静压与降噪效果列表Table 2 Comparison of far-field maximum pressure and noise reduction effect
3 准三维计算结果的机理分析
3.1 近场分析
距飞行轨迹50m截面的静压曲线(图10、图11)来看,根据细长杆形状不同,无细长杆方案有单个波峰,加装细长杆后头部激波被"分裂"成几个较小的波峰。也就是说,在近场,无细长杆模型的激波强度较强,而通过加装细长杆,就可以把激波"分解",这样就能够有效地降低激波强度,减少其近场的噪声。而多道激波在中场叠加并影响远场的情况将在本文3.3讨论。
连续压缩(一阶连续)方案的近场激波强度最小,这样的结果与细长杆形状有关。图12为细长杆以及机头前部流场静压云图,由于细长杆前段对气体的连续压缩,产生了多道较弱的压缩波,这些压缩波最终会叠加为激波。从数值模拟的结果来看,这些压缩波在叠加为激波之前受到了膨胀波系的影响而产生了弯折。多道压缩波叠加相当于对机头的来流进行了“预压缩”,使得机头所产生的激波大为减小。从云图中还可以发现,外形一阶连续的细长杆相对于有锐边的细长杆更能够产生连续的更弱膨胀波,使机头前的气流密度和温度不至于降低太多,就能够降低机头产生的激波强度,这就是这个方案可以降低音爆噪声的主要机理。
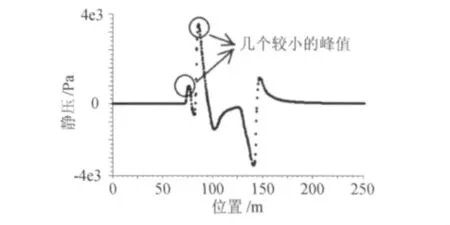
图11 带细长杆近场静压曲线Fig.11 Near-field static pressure curve of aircraft with slender-rod-noise-reduction

图12 静压云图中的压缩波、激波、膨胀波系Fig.12 Compression wave,shock wave,expansion wave system in the static pressure cloud
3.2 远场分析
从熵增和耗散的角度来解释本文第2部分发现的规律,连续压缩模型之所以具有低噪声的优势,是因为它可以使气体压缩过程接近于等熵过程,总压损失小,噪声水平也就较低[9];双锥体方案的锥顶角直接影响到了气流转折角,转折角越大,气体压缩过程中的熵增越多,能量的耗散也越多,因此锥顶角越大,噪声也越大;而双台阶体方案降噪效果较差也可以用这样的理论来解释。这就解释了越是平滑的外形,具有越好的降噪效果。以上是从能量耗散的角度解释噪声,本文3.3将从激波强度的角度来解释降噪的机理。
3.3 近场对远场的影响分析
这里以连续压缩(一阶连续)的模型为例,分析从近场激波到远场激波的演变过程。图13分别展示了距飞行轨迹50m、75m、100m的静压曲线,观察这三条静压曲线可以发现两道激波逐渐收敛合并的过程。距飞行轨迹50m的两个静压峰值还十分明显,但到75m处时静压曲线已经比较靠近,客机扰动传播到距飞行轨迹100m位置的静压峰值基本已经相互融合。这样的现象在各类细长杆方案中都可见,这与激 波叠加的基本理论完全一致。

图13 50m处静压曲线、75m处静压曲线、100m处静压曲线Fig.13 Static pressure curve of the distance 50m,75m,100mfrom the flight path
由于远场的激波是近场的各压缩波叠加而成的,因此噪声水平实质上取决于细长杆产生的激波强度与机头产生的激波强度,这与Page和Plotkin的研究成果[10]相符。为了了解近场参数和远场参数之间关系,这里以静压参数为例尝试探究经验公式。为了经验公式的有效性,只观察细长杆产生的近场静压超过1000Pa并且有明显的两个近场峰值的情况。以二阶线性方程回归公式得到远场(距飞行轨迹1200m处)静压峰值与近场(距飞行轨迹50m处)两个静压极值之间的关系:

这里已经考虑了单位的统一性,单位为Pa。经过数据回归分析,计算出:
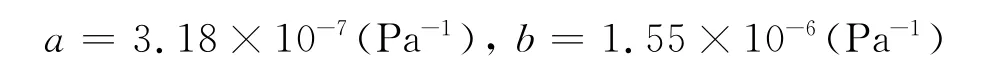
通过上面的分析,我们知道远场激波强度是与细长杆激波强度和机头激波强度密切相关的。这个经验公式也可以作为细长杆初步设计时的参考。
4 三维计算
准三维流场计算虽有高效率的优点,但不及三维计算有说服力,况且带攻角的细长杆降噪流场分析已经不属于准三维流场范畴,对带细长杆客机采取三维分析是有必要的。本章选择了降噪效果最佳的5°半顶角双锥体细长杆方案和本文独创的连续压缩的方案,分析这两种方案的三维流场,并对带攻角的模型分析气动力。
细长杆降噪需要远场计算结果,由于我们只关心飞机噪声向地面传播方向的流场情况,且客机流场属对称问题,切割一半并去除上部以减小计算域。得到的零攻角时连续压缩的流场静压分布情况与第4部分中连续压缩细长杆准三维模型静压情况相符合,说明了准三维轴对称简化是合理且可行的。零攻角时1200m外远场地面的静压分布如图14,可以从地面的静压分布中观察出准三维问题中的“N波”特性,这与准三维模拟是吻合的,也是对准三维模型计算方法的验证。5°攻角时,双锥体细长杆的气动力如图15。由于强度校核属于气动弹性范畴,本文主要阐述细长杆的降噪效果与降噪机理,故这里不展开说明。
图14 零攻角时1200m外远场地面的静压分布Fig.14 Static pressue distribution at the distance of 1200mfrom the flight path while AOA of aircraft is 0°
5 结 论
本文从第1部分开始对超声速客机进行数值模拟,验证了数值模拟的可信性,第2部分介绍了各类细长杆设计方案及其设计理由,并建模计算,展示了计算结果,第3部分从气体动力学理论出发解释了细长杆降噪的内在机理并总结出经验公式,第4部分基于三维分析。经过大量数值模拟以及理论分析,本文获得了以下结论:
(a)合理的细长杆方案具有降噪作用。
(b)不同形状的细长杆在远场的激波角基本相同。
(c)小顶角双锥体细长杆降噪效果较好。
(d)台阶数多的台阶体细长杆噪效果较好。
(e)外形光滑细长杆降噪效果较好。
(f)细长杆降噪机理在于将原本机头的单道激波“分解”为多道较弱的压缩波,使它们在远场叠加后的激波强度较无细长杆的模型弱。
(g)近场峰值与远场峰值之间的关系基本满足本文3.3中的经验公式。
我国目标要跻身于航空大国之列,将来也一定会发展超声速民用飞机,超声速客机细长杆降噪具有降噪效果明显以及对机身改动小的优点,拥有广阔的应用前景。本文只讨论了细长杆降噪方法,事实上超声速客机的降噪方法有许多。比如使用更为细长机身以减小截面积、使用小型化的客机、加大起飞攻角等措施,这些都是值得探究的方向。关于细长杆的进一步分析还可以是细长杆附加阻力研究、细长杆热疲劳分析、减重方法探究、近场与远场经验公式的修正、改进和推广。而将细长杆用于实际飞机型号进行试验才是证明理论研究的最好方法。在噪声污染日益严重的今天,研究并应用超声速飞机的降噪方法无疑具有重大意义。
[1]KENNETH J PLOTKIN.State of the art of sonic boom modeling[A].Sonic Boom Symposium,136th Meeting of the Acoustical Society of America[C],2001,(4):530-536.
[2]TAYLOR A D.The TRAPS sonic boom program[J].NOAATechnicalMemorandumERL-87,1980:1-B18.
[3]ROBINSON L D.A numerical model for sonic boom propagation through an inhomogeneous windy atmosphere[J].InNASA.LangleyResearchCenter,High-SpeedResearch:SonicBoom,1992,(1):7-30.
[4]PLOTKIN,KENNETH J.PCBoom3sonic boom prediction model-version 1.0c[J].WyleResearchReport WR95-22E,1996,(937):255.
[5]PRESTON A HENNE.Case for small supersonic civil aircraft[J].JournalofAircraft,2005,42(3):765.
[6]黄江涛,高正红,苏伟.几种典型的迎风格式比较[J].航空计算技术,2008,38(1):1-2.
[7]WHITHAM G B.The flow pattern of a supersonic projectile[J].Commum.PureAppl.Math.,1952,(3):301-348.
[8]WHITHAM G B.On the propagation of weak shock waves[J].JournalofFluidMechanics,1956,(1):290-318.
[9]林兆福.气体动力学[M].北京:北京航空航天大学出版社,1988:187,256.
[10]PAGE J A,PLOTKIN K J.An efficient method for incorporating computational fluid dynamics into sonic boom prediction[R].AIAA-91,327,1991:17.

