基于干扰观测器的高超声速飞行器非线性控制

宋超, 赵国荣, 黎志强, 周源

(1.海军航空工程学院 控制工程系, 山东 烟台 264001;2.国防科学技术大学 机电工程与自动化学院, 湖南 长沙 410073)

基于干扰观测器的高超声速飞行器非线性控制

宋超1, 赵国荣1, 黎志强2, 周源1

(1.海军航空工程学院 控制工程系, 山东 烟台 264001;2.国防科学技术大学 机电工程与自动化学院, 湖南 长沙 410073)

针对高超声速飞行器非线性动力学系统中存在的高度非线性、多变量耦合及参数不确定等问题,结合反演滑模控制,利用非线性干扰观测器对各种干扰的逼近特性设计了一种飞行器反演滑模控制器。该控制器利用干扰观测器观测系统的干扰时,放宽了现有文献对干扰的界进行限制的苛刻条件,未观测出的部分干扰采用反演滑模控制进行补偿,避免了累积误差,实现对制导指令的鲁棒输出跟踪,并证明了系统稳定性。仿真结果验证了该方法能较理想地观测干扰,保证系统良好的鲁棒性。

高超声速; 干扰观测器; 反演设计; 滑模控制

引言

近年来,高超声速飞行器作为突破导弹防御系统并实现远程精确打击的新途径已成为研究的热点[1]。为满足近空间再入飞行的力学和热学环境要求,高超声速飞行器需要以大迎角再入大气层内,因此,飞行环境的大范围变化、机身的弹性变形、气动参数的变化和外界干扰都不可避免,致使所建立的飞行器动力学模型存在高度非线性、强耦合及不确定性,且表现为非匹配的不确定性[2-3]。高超声速飞行器飞行参数耦合强烈,且随时间变化剧烈,是多变量的强耦合非线性时变系统[4]。传统的基于动态逆解耦的三通道独立设计方法不再适用,必须采用非线性控制方法设计满足性能指标要求的控制器。非线性干扰观测器(Nolinear Disturbance Observer, NDO)技术用于消除系统的未知干扰和未建模动态等不确定因素的影响,在很多领域得到应用[5-8]。但是,现有文献在利用非线性干扰观测器时,大多要求对干扰的界做出限制,即假设干扰为未知但是有界的,这大大限制了干扰观测器的应用领域。

在对飞行器数学建模过程中,本文综合考虑飞行过程中遇到的各种不确定性,采用干扰观测器对系统的干扰进行估计,并放宽了干扰观测器对干扰的界的限制,未观测出的部分干扰采用反演设计[9]与滑模变结构控制[10-11]方法补偿,实现了高超声速飞行器的鲁棒控制。

1 飞行器数学模型的建立

为了使描述飞行器在空间的六自由度运动方程不过于复杂,作如下假设:

(1)飞行器再入过程中,地球为平面且静止;

(2)不考虑飞行器的挠性,即视为刚体;

(3)忽略操纵面的转动惯量,高超声速飞行器的惯性主轴就是机体轴,无惯性积。

(1)

(2)

式中,a=1/(JxJy);b=1/Jz;Jx,Jy,Jz为机体轴的主转动惯量;其余参数说明见文献[12-13]。

简化式(1)和式(2),并考虑气动参数的不确定性,则系统模型可写为:

(3)

f2(x1,x2)+Δf2(x2)+g2(x1)u+Δ2(x1,x2,t)

(4)

y=x1

(5)

式中,f1(x1),f2(x1,x2),Δf2(x2),g1(x1),g2(x1)为对应的矩阵;Δ1(x1,t),Δ2(x1,x2,t)为非匹配不确定项。

令

d1=Δ1(x1,t),d2=Δf2(x2)+Δ2(x1,x2,t)

式中,d1为气动参数误差;d2为模型不确定性及外界干扰等不确定项总和。

飞行器控制系统的任务是在不超过控制执行机构所能提供的控制量限制的前提下,实现对制导系统给出的气流角指令yd的跟踪[14]。

2 反演滑模控制系统设计

2.1 非线性干扰观测器设计

由文献[6-7]的结论,非线性干扰观测器的设计原理如图1所示。由图1可知,为消除不确定性和未知干扰对系统性能的影响,首先采用干扰观测器对系统的干扰进行估计,未观测出的部分干扰使用滑模控制来补偿。

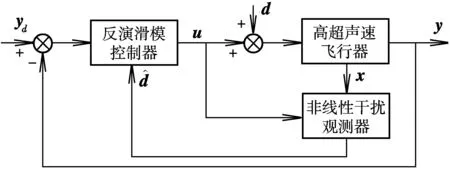
图1 基于非线性干扰观测器的控制结构图

定义辅助变量

设计非线性干扰观测器如下:

(6)

(7)

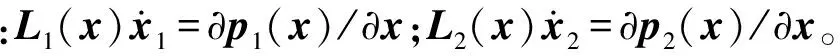
为证明观测器的稳定性,定义非线性干扰观测器的观测误差为:

(8)

同理可得:

(9)

构造Lyapunov函数:

对其求导并将式(8)和式(9)代入得:

(10)

由式(10)可知,通过适当选择L1(x)>0,L2(x)>0可以使观测器的观测误差按指数收敛。简单起见,选择L1(x)=c1,L2(x)=c2(c1,c2为正常数),设计p1(x)=c1x1,p2(x)=c2x2。

2.2 反演滑模控制系统设计

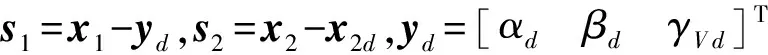
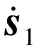
(11)

设计虚拟控制量为:

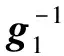
(12)

将式(12)代入式(11),得:

(13)

对s2求导,得:

(14)

设计控制律为如下形式:

(15)

2.3 控制稳定性分析

对式(3)～式(5)的系统,考虑Lyapunov函数:

对V求导并将式(13)～式(15)代入,得

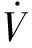
≤-(k1-0.25)‖s1‖2-(k2-0.25)‖s2‖2-

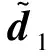
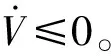
3 仿真验证

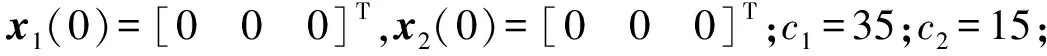
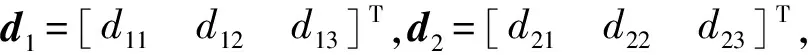
仿真结果表明,本文设计的干扰观测器能很好地对各种干扰进行观测,整个系统具有良好的跟踪性能,跟踪指令时不但上升时间较短,而且超调量和跟踪误差也很小。对比采用干扰观测器前后的姿态角跟踪曲线,可以看出本文设计的控制器具有更好的鲁棒性,能够更好地克服系统中参数不确定性和外来干扰。

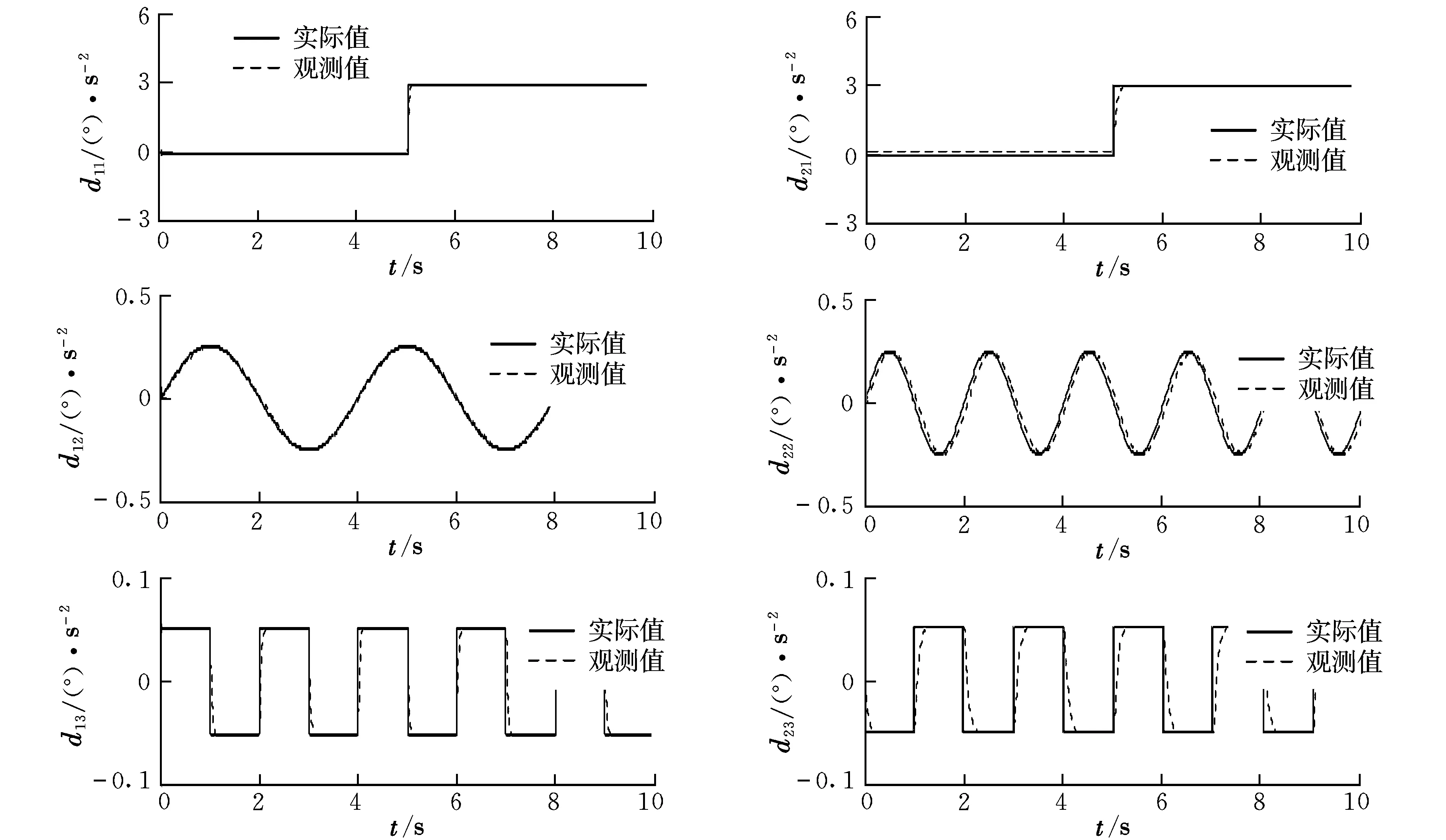
图2 干扰观测器对干扰d1和d2的观测曲线

图3 采用干扰观测器前后的姿态角跟踪曲线

4 结束语

本文在对高超声速飞行器数学模型充分分析的基础上,设计了非线性干扰观测器对各种干扰进行观测,并放宽了现有文献中对干扰的界的限制,采用反演滑模控制策略,通过设计虚拟控制,将输出误差限制在很小的范围内,并最终设计真正的控制律。研究表明,采用干扰观测器后能对系统各种未知干扰和气动参数的不确定性进行补偿,系统性能得到明显改善。由仿真结果可以看出,该控制器具有良好的跟踪性能,对不确定性及外界干扰具有鲁棒性。

[1] Jorris T R.Common aero vehicle autonomous reentry trajectory optimization satisfying waypoint and no-fly zone constraints[D].Alabama:Air University,2007.

[2] Maj Mirmirani,Chivey Wu.Modeling for control of a generic airbreathing hypersonic vehicle[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit.San Francisco,California,2005:1-19.

[3] 张军,王玫,赵德安.高超飞行器的再入非线性鲁棒控制[J].动力学与控制学报,2011,9(1):91-96.

[4] Shahriar Keshmiri,Richard Colgren,Maj Mirmirani.Six-DOF modeling and simulation of a generic hypersonic vehicle for control and navigation purposes[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit.Keystone,Colorado,2006:1-10.

[5] Nikoobin A,Haqhiqhi R.Lyapunov-based nonlinear disturbance observer for serial n-Link robot manipulators [J].Journal of Intelligent and Robotic System:Theory and Application,2009,55(2-3):135-153.

[6] Chen Wenhua,Ballance D J,Gawthrop P J.A nonlinear disturbance observer for robotic manipulators [J].IEEE Transactions on Industrial Electronics,2000,47(4):932-938.

[7] Chen Wenhua.Nonlinear disturbance observer-enhanced dynamic inversion control of missiles [J].Journal of Guidance,Control,and Dynamics,2003,26(1):161-166.

[8] 张元涛,石为人,邱明伯.基于非线性干扰观测器的减摇鳍滑模反演控制[J].控制与决策,2010,25(8):1255-1260.

[9] Baohua L,Hyochoong B,John E,et al.Adaptive backstepping control based autopilot design for reentry vehicle[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit.Rhode Island,Providence,2004:1-10.

[10] Capisani L M,Ferrara A,Maqnani L.Design and experimental validation of a second-order sliding-mode motion controller for robot manipulators [J].International Journal of Control,2009,82(2):365-377.

[11] 方勇纯,卢桂章. 非线性系统理论[M].北京:清华大学出版社,2009:21-81.

[12] 钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2008:28-48.

[13] 赵汉元.飞行器再入动力学和制导[M].长沙:国防科学技术大学出版社,1997:23-86.

[14] 陈洁,周绍磊,宋召青.基于不确定性的高超声速飞行器动态面自适应反演控制系统设计[J].宇航学报,2010,31(11):2550-2556.

(编辑：崔立峰)

Nonlinearcontrollawforhypersonicvehiclewithnonlineardisturbanceobserver

SONG Chao1, ZHAO Guo-rong1, LI Zhi-qiang2, ZHOU Yuan1

(1.Department of Control Engineering, NAAU, Yantai 264001, China;2.College of Mechatronics Engineering and Automation, NUDT, Changsha 410073, China)

Hypersonic vehicle’s nonlinear dynamics system is highly nonlinear, multivariable coupled and includes uncertain parameters. Particularly for this problem, a new backstepping sliding mode controller is designed based on nonlinear disturbance observer (NDO) and backstepping sliding mode control scheme. NDO is used to observe the disturbance of the system and the limitation of the disturbance can be unknown. Sliding mode control is adopted in every backstepping design to compensate for unknown disturbance. The approach prevents cumulative error and realizes robust output tracking to guide order. The system is proved to be stable. Simulation results show this method can observe the disturbance ideally and enhance the robust performance of system.

hypersonic; disturbance observer; backstepping; sliding mode control

TP273

A

1002-0853(2012)06-0546-05

2012-02-10;

2012-07-04; < class="emphasis_bold">网络出版时间

时间:2012-11-23 14∶01

国家自然科学基金资助(61004002);航空科学基金资助(20110184001)

宋超(1983-),男,山东荣成人,博士研究生,研究方向为飞行器制导与控制。