中国碳排放的影响及预测研究

■ 牛苗苗/杨树旺

（中国地质大学（武汉）经济管理学院，湖北 武汉 430074）

0 引言

由于中国经济总量增长迅速，能源消耗不断增加，再加上以煤为主的能源消费结构，导致碳排放总量不断增长，成为世界上最大碳排放国家之一[1]。虽然目前中国尚未承担减排任务，但是减少碳排放已成为国际共识，中国也面临着巨大的挑战和压力。积极寻找减排途径、加速发展低碳经济，既是中国顺应世界发展潮流的需要，也是中国实现可持续发展的内在要求。寻找减排途径的前提，是准确分析和把握中国碳排放量的影响因素，并对其碳排放量进行预测，这样才能对症下药。为此，本文运用协整分析方法，定量研究了各因素对碳排放量的影响，并利用ARIMA模型对中国碳排放总量进行预测。

1 中国碳排放影响因素分析

1.1 变量选取

选取二氧化碳排放总量（TC）为目标变量，人口总数（P）、国内生产总值（G）、能源消费总量（E）、能源生产效率（EP）、产业结构（ST，用工业比重作为代表）为解释变量。

1.2 数据的选取

本文选取1980—2011年年度数据，数据来源于《2012年中国统计年鉴》和美国能源总署EIA的统计结果，均以1980年为基期。同时，为消除变量中的不稳定性和异方差现象，对各变量分别进行对数化处理，软件使用Eviews5.0。

1.3 实证分析

1.3.1 相关性检验

通过相关系数矩阵的计算，可以发现，TC与P、G、E、EP的相关系数都在0.73以上，而TC与ST的相关系数较小，相关性较弱。同时，可以发现E、EP、G和P这些解释变量的相关系数也很高，可能存在较严重的多重共线性。为了减轻多重共线性的影响，在建立协整方程时，应采用逐步回归法。

1.3.2 平稳性检验

利用Eviews5.0来检验，结果发现TC、P、G、E、ST和EP经过二阶差分后都是显著平稳的。在此基础上，使用A D F检验方法，可以发现TC、P、G、E、ST和EP的水平序列在1%和5%的显著性水平上都不平稳，一阶差分DTC、DP、DG、DE、DST、DEP在1%的显著性水平都是不平稳的，二阶差分DDTC、DDP、DDG、DDE、DDST、DDEP在1%的显著性水平上都是平稳的，也就是说这些时间序列TC、P、G、E、ST和EP经过二阶差分后平稳，它们都是二阶单整序列。这意味着协整检验是有必要的。

1.3.3 协整检验

本文采取Engle和Granger提出的协整检验方法。这种检验方法是对回归方程的残差进行单位根检验。从协整理论的思想看，自变量和因变量之间存在协整关系，也就是说，因变量能被自变量构成的线形组合所解释，两者之间存在稳定的均衡关系，因变量不能被自变量所解释的部分构成一个残差序列，这个残差序列应该是白噪声的，平稳的[2]。因此，检验一组变量(因变量和自变量)之间是否存在协整关系等价于检验回归方程的残差是否是平稳序列。由于TC、P、G、E、ST和EP均为二阶单整变量，我们可按EG两步法做如下协整回归，并检验三个变量是否存在协整关系。

第一步，为了减轻多重共线性的影响，利用Eviews5.0软件进行逐步回归[3]。逐步回归后，剔除了P和ST两个变量。修正多重共线性影响后的协整方程为：

方程括号中为估计参数t的统计量，由于各变量之间的量纲差异较大，所以有必要对原始数据进行标准化处理，标准化后的协整方程为：

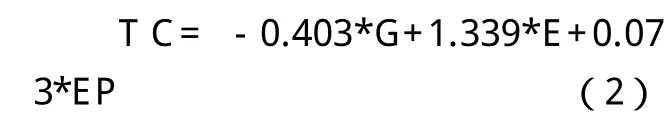
从式(1)可以看出，回归方程的T检验和F统计检验都很显著，而且修正的可绝系数也很高，说明拟合总体效果较好。DW=1.886016接近于2，说明模型不存在自相关。但是，G的系数是负，EP的系数是正的。这可能是因为方程(1)中没有考虑到GDP和能源生产率对碳排放量影响的时滞性造成的结果。

第二步，回到协整检验，对方程(1(的残差Ut进行白噪声检验。如表1所示，Ut序列在1%显著性水平下拒绝原假设，因此可以判定Ut为白噪声的平稳序列。同时从残差Ut的自相关图和偏相关图也可以看出，残差Ut是白噪声的。这表明TC与E、G、EP之间存在一定的协整关系，即它们之间的某种线性组合是平稳的，它们变动的方向与幅度一致，长期上存在稳定的线性关系。（参见表1）

1.3.4 向量自回归

向量自回归(V A R)模型不但考虑到影响因素的滞后问题，还能够解决自变量内生的问题。本文所分析的各种影响因素对碳排放的影响基本上都存在一定的时滞，并且碳排放和本文分析的影响因素之间关系复杂，存在自变量内生的问题。所以，本文将进一步考虑建立向量自回归(VAR)模型。对由TC与G、E、EP组成的VAR方程，通过Eviews5.0反复试验，在选择滞后期为1时，SC最小，则确定滞后期为1的VAR模型。估计结果如下，其具体形式可以表述为如下模型:

表1 残差Ut的ADF检验

另外，通过VAR模型的稳定性检验也可以发现，VAR模型有两个特征根落在单位圆之外，表面所建立的模型是非平稳系统。（见图1）

下面对T C与G、E、E P做一阶差分，利用一阶差分序列建立VAR模型。根据AIC和SC最小原则，本文选择滞后期为1的VAR模型，估计结果如下：

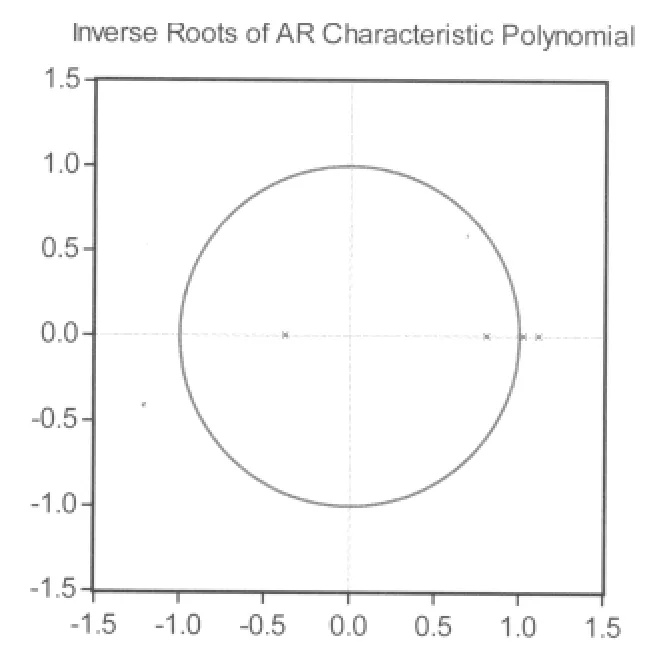
图1 VAR模型的稳定性检验

从表2可以看出，一阶差分后得到的VAR方程的调整后的样本决定系数为0.527948，AIC和SC也非常小，可以判断VAR模型的总体性质比较好。同时从V A R模型的稳定性检验也可知，VAR模型的全部特征根都在单位圆之内，表明VAR模型是稳定的。所以该模型较好地反映了中国碳排放复杂系统的长期变动关系，并且较好地解决了自变量内生化的问题。

2 中国碳排放的预测

2.1 ARIMA模型的识别

由上一章平稳性检验可以看出TC二阶差分后是白噪声的，这也意味着利用其来做预测是没有意义的。所以对TC原始数据取对数,即得LNTC，然后对LNTC进行ADF检验。由表3可知，在5%显著性水平上，LNTC一阶差分后是平稳的。因为是进行了一阶差分,因此认为A R I M A(p,d,q)中d=1。

ARMA(p,q)模型的识别与定阶可以通过样本的自相关与偏自相关函数的观察获得[4]。通过LNTC一阶差分后的自相关结果可以发现，偏自相关在滞后1处冒出了统计上显著的尖柱，而在其余地方都不显著。根据A C F与P A C F的理论模式，可初步认定DLNTC模型是一个AR(1)过程。

2.2 AR(1)模型的估计

首先，尝试建立如下AR模型：

DLNTCt=δ+α1DLNTCt-1+μt利用Eviews5.0，我们得到如下估计结果：

表2 VAR模型估计统计量

2.3 模型的检验

通过检验结果可知，对模型的Q统计量进行白噪声检验，得出残差序列相互独立的概率很大，故不能拒绝序列相互独立的原假设，即表明估计出来的残差是纯随机的，模型检验通过，也就是说，将DLNTC设定为AR(1)过程是正确的，故可以利用方程(5)来预测中国碳排放量。

2.4 模型的预测

我们使用时间序列分析的方法对中国碳排放的年度数据序列建立自回归预测模型，并利用方程(5)对2005到2008年的数值进行预测和对照：

由表4可见，该模型在短期内预测比较准确，平均绝对误差为2.99%。按照所建立的模型，我们对中国2012年与2013年的碳排放总量进行预测：2012年预计碳排放总量为6872.479百万吨，2013年预计碳排放总量达到7252.646百万吨。

3 结论

通过协整分析，发现中国碳排放量与中国国内生产总值、中国能源消费量、中国能源生产率之间存在长期均衡关系。其中中国能源消费量对中国碳排放量有显著的正向影响，而中国国内生产总值对中国碳排放量的影响具有较强的滞后性。同时研究发现，利用ARIMA模型对中国碳排放量的预测精确度相当高，按照所建立的ARIMA模型预测，2012年预计中国碳排放总量为6872.479百万吨，2013年预计碳排放总量达到7252.646百万吨。

表3 ADF检验结果

表4 ARIMA（1,1,0）预测值与实际值的比较

[1]王锋，吴丽华.中国经济发展中碳排放增长的驱动因素研究[J].经济研究，2010(2)：123-131.

[2]达摩达尔·N·古扎拉蒂.计量经济学基础[M].北京：中国人民大学出版社,2005.

[3]申笑颜.中国碳排放影响因素的分析与预测[J].统计与决策，2010(19):90-92.

[4]谭诗!.ARIMA模型在湖北省GDP预测中的应用——时间序列分析在中国区域经济增长中的实证分析[J].时代金融，2008(1):26-27.