几何非线性大转动变形分析

祁继鑫 彭兴勇

(1.天津市津南区建筑勘察设计所，天津 300350;2.中国建筑第一局(集团)有限公司，北京 100161)

0 引言

作为计算力学的重要分支，有限单元法是一种将连续体离散化以求解各种力学问题的数值方法。1960年Clough在研究平面弹性问题时提出了“有限单元法”的概念。如今，有限单元法已经成为处理力学、物理、工程等计算问题的有效方法之一[1-4]。

早期的几何非线性有限元分析基本上仍是线性分析的扩展。近年来，基于非线性连续介质力学原理的有限元分析有了很大的发展，并且已经有效地应用于广阔的领域[2]。

本文以几何非线性余能原理作为基础，采用全量法，对一悬臂曲梁自由端部受弯矩作用而产生大转动变形的数值算例进行了分析，验证了该原理适用于解决具有曲线边界的几何非线性的问题。

1 数学模型的建立

1.1 将单元余能分解为转动部分和变形部分

1.2 柔度矩阵

单元柔度矩阵的显式表达式为[5]:

其中，E，v分别为材料的弹性模量和泊松比;U为单位张量。

1.3 支配方程

利用Lagrange乘子法，放松平衡条件约束，则修正的泛函可写成:

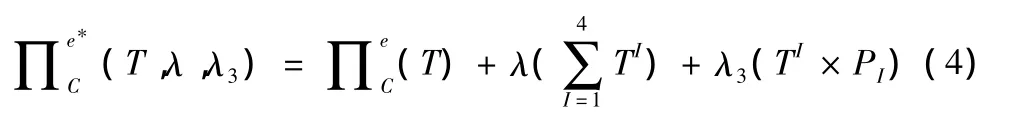
其中，λ，λ3均为 Lagrange乘子，λ =λ1e1+λ2e2。

系统的修正泛函为:

由修正的余能原理，泛函的驻值条件可写为:

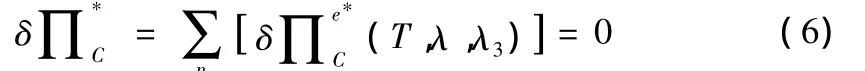
式(6)即为基于基面力概念的余能有限元控制方程[5]。

2 数值算例分析

有一悬臂曲梁的自由端部受弯矩作用如图1所示，该悬臂曲梁的半径为R=100 m，圆心角为90°，截面的高度为h=1 m，弹性模量E=2 000 N·m2，泊松比v=0，作用在自由端的弯矩值为M=2EI/R=3.333 3 N·m。计算时取单位厚度，假设按平面应力问题考虑，采用迭代法计算并进行一次加载分析。

计算时将该悬臂曲梁剖分为140个四边形单元、307个边中节点(如图2所示)，采用全量法进行计算分析，结果为一次加载所得。下面将用本文方法计算所得悬臂曲梁自由端的无量纲水平位移值u/(0.5πR)、无量纲竖向位移值v/(0.5πR)与无量纲荷载值k=2MR/(5EI)的关系列于表1，图3为悬臂曲梁的荷载—水平位移曲线，图4为该悬臂曲梁对应不同加载值k的变形全图。

表1 端部承受集中弯矩悬臂梁的荷载—位移关系

图1 端部承受弯矩的悬臂曲梁

图2 四边形单元剖分的曲梁

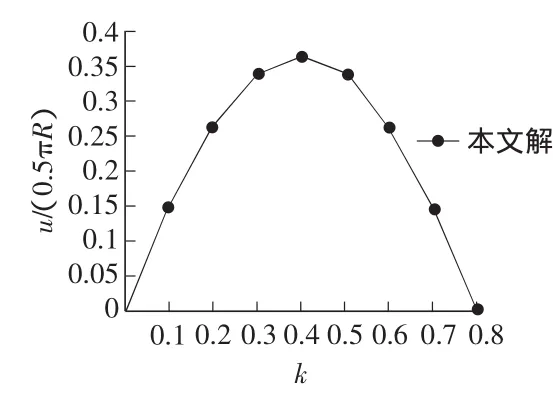
图3 悬臂曲梁的荷载—水平位移曲线

图4 悬臂曲梁的变形全图

3 结语

1)从表1及图3和图4可以看出，当施加荷载到k=0.4时，该曲梁变形为直梁，梁端的水平位移达到最大值:0.363 1，竖向位移为:0.637 5;当继续施加荷载到k=0.8时，该曲梁反向弯曲，其当前位形与初始位形呈对称状，此时，梁自由端的水平位移为0，而竖向位移约为荷载k=0.4时梁自由端竖向位移的两倍，即:1.273 3。

2)该数值算例研究表明，利用本文给出几何非线性余能原理有限元公式可以解决具有曲线边界的几何非线性大转动变形问题，且能得到较高精度的解，对于解决结构稳定性和屈曲问题的几何非线性大变形分析具有重要的理论和实际意义。

[1] ZIENKIEWICZ O C.The finite element method[M].New York:McGraw-Hill，1977.

[2] 王勖成.有限单元法[M].北京:清华大学出版社，2003.

[3] COOK R D.Concepts and applications of finite element analysis[M].New York:Wiley，1981.

[4] BATHE K J.Finite element procedures[M].New Jersey:Prentice-Hall，1996.

[5] 彭一江.基于基面力概念的新型有限元方法[D].北京:北京交通大学，2006:4.