关于一类微积分计算方法的探究

席高文

（重庆科技学院，重庆401331）

关于一类微积分计算方法的探究

席高文

（重庆科技学院，重庆401331）

通过对一类微积分计算方法的探究，从本质上分析所形成的思维模式,给出了一元微分以及积分区域为圆的二重积分通过平移变换简单巧妙的计算方法。由此可以类比出多元微分，以及多重积分的计算方法。

微分；导数；积分；平移；求导法则

1 微分计算方法的探究

微分的计算，关键就是导数的计算，教材中给出了许多求导法则，例如：和、差、积、商的求导法则，复合函数、反函数、隐函数、参数方程的求导法则等。在教学中，如何让学生掌握求函数导数的核心，是我们要研究的关键问题。首先要让学生熟练掌握求导法则的核心，其次是掌握求导的基本方法。

首先，对于求导法则，除了和、差、积、商的求导法则外，对于复合函数、反函数、隐函数以及参数方程的求导法则，从求导的本质来看，最主要的就是复合函数的求导法则，而反函数、隐函数以及参数方程的求导法则，完全可以由复合函数的求导法则得到。复合函数的求导法则为：如果函数u=g(x)在点x可导，而函数y=f(u)在点u=g(x)可导，则复合函数y=f(g(x))在点x可导，且其导数为

即函数y=f(g(x))对x的导数是y=f(u)对中间变量u的导数乘以函数u=g(x)对自变量x的导数。在复合函数求导法则的基础上，其他几个求导法则，只需要作一些简单的变化即可得到。例如：对于隐函数求导法则，即为在对函数求导时，如果变量y是x的函数，求导时遇到变量y，只需要把变量y看作中间变量，首先是函数对变量y求导，然后再乘以变量y对自变量x的导数；对于参数方程的求导法则，如果变量y和x都是参数t的函数，在求函数的导数时，只需要把变形为，把参数t看作中间变量，即有函数的导数是变量y对参数t的导数，除以变量x对参数t的导数；对于反函数的求导法则，如果变量y是x的函数，在求函数的导数时，可以转化为，即函数的导数是所给函数用y表示x后，变量x对变量y的导数的倒数。

其次，就是要掌握求导数的基本方法和步骤：第一步，观察所给的解析式是否为两个及两个以上函数的和、差、积、商。如果是，则运用导数的运算法则，转化为求“形式上为某一个基本初等函数”（指由常数函数、幂函数、指数函数、对数函数、三角函数和反三角函数等基本初等函数复合而成的初等函数）的求导问题；第二步，利用基本初等函数的求导公式以及复合函数的求导法则，求其导数，直到所求函数为“标准的基本初等函数”（指函数形式为y=xp（p∈R是常数），y=ax（a＞0且a≠1），y=log ax（a＞0且a≠1），y= sin x，y=arcsin x等）为止。即在运用复合函数求导法则的中间变量为自变量x时求导结束。

例1 设隐函数y=sin(x+y)，求y′。

解：由于函数y=sin(x+y)是一个形式上的三角函数，y是x的隐函数，因此两端对x求导得

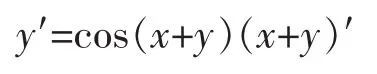
函数x+y是两个函数的和函数，利用求导的运算法则得

这里函数x已经是一个标准的幂函数，而函数y不仅是x的隐函数，而且是形式上的幂函数，故

即

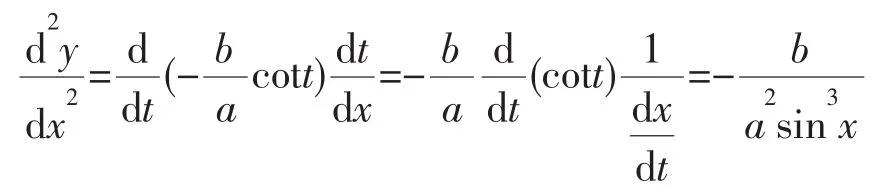
例3已知y=xsinx，求

解：对于y=xsinx，由于不是形式上的某类基本初等函数，无法直接求导，因此，必须作恒等变形，才可以利用求导法则进行求导。这种恒等变形一般有两种方法。

方法一：两端取对数得：ln y=sin x ln x，上式两边对x求导得（y是x的隐函数)，则

这里利用了积的求导法则。

方法二：因为y=elnxsinx，所以

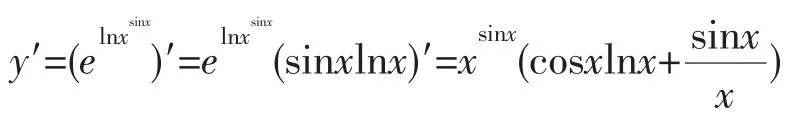
这里利用了函数y=elnxsinx是个形式上的指数函数。

2 积分计算方法的探究

解析几何是通过建立坐标系，使点与实数对之间一一对应，以及曲线与方程之间一一对应，运用代数方法研究几何问题，或用几何方法研究代数问题。解析几何的建立第一次真正实现了几何方法与代数方法的结合，使形与数统一起来，这是数学发展史上的一次重大突破。

解析几何分为平面解析几何与空间解析几何两部分内容，本文以空间解析几何为主加以讨论。如果空间内一点P的旧坐标与新坐标分别为P(x,y,z)与P (x′,y′,z)，则平移变换的公式为或者显然，平面上任何一条曲线f(x，y)=0，或者空间任何一个曲面f(x，y，z)=0，经过平移变换后得到的新方程f(x′,y′)=0、f(x′,y′,z′)=0分别表示的是同一条曲线、同一个曲面。

在计算二重积分时，当积分区域为圆形区域，且圆心不在原点时，无论是直角坐标系或者极坐标系下，直接计算，都比较复杂，但是，如果利用平移变换，则计算会非常简单。

解：如图1所示，积分区域为圆x2+y2=2y，此圆的圆心在（0，1），半径为1。一般的方法是利用极坐标系计算（利用直角坐标系计算更复杂）。

这里应用了当函数f（x）=0为奇函数，且积分区域D关于y轴对称时，，以及定积分的计算公式。

当我们巧妙的利用平移变换后，计算就会变的非常简单，即有

图1 积分区域D

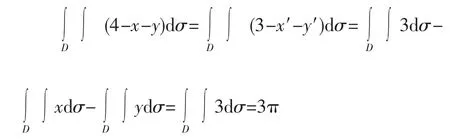
这里同样应用了当函数f（x）=0为奇函数，且积分区域D关于y轴对称时，；当函数f（y）=0为奇函数，且积分区域D关于x轴对称时，

图2 积分区域D′

类似于例4的问题非常多，这里不再赘述。由此可见，如果教师能够引导学生认真探究微积分计算方法的本质，不仅可以使学生牢固掌握其计算方法，而且开阔了学生的视野，进一步培养了学生的创新能力、分析能力以及解决实际问题的能力。

[1]同济大学数学系.高等数学：第六版[M].北京：高等教育出版社，2007.

[2]华东师范大学数学系.数学分析[M].北京：高等教育出版社，2001.

Research on the Calculation M ethod of Calculus

XIGaowen
(Chongqing University of Science and Technology,Chongqing 401331)

In this paper,by study on the calculation method of calculus,and thinking model,we obtain single differential,and the calculation method of double integration whose integration domain is circular through the translation of coordinates.Hence,based on it,the calculation of the Multivariate differentialandmultiple integral can be obtained.

differential；derivative；integral；translation；derivation rules

O172

A

1673-1980（2012）03-0177-03

2012-02-21

席高文（1963-），男，河南灵宝人，教授，研究方向为组合数学。