三维侧位抛物线型方位漂移轨道设计的数值算法

鲁 港，夏泊洢

(1.中国石油辽河油田公司勘探开发研究院，辽宁盘锦 124010;2.中国石油长城钻探工程有限公司工程技术研究院，辽宁盘锦 124010)

三维侧位抛物线型方位漂移轨道设计的数值算法

鲁 港1，夏泊洢2

(1.中国石油辽河油田公司勘探开发研究院，辽宁盘锦 124010;2.中国石油长城钻探工程有限公司工程技术研究院，辽宁盘锦 124010)

考虑方位漂移因素的设计约束方程组是一个具有3个独立未知数、多个隐含未知数的非线性方程组，需要使用数值迭代法才能求出其数值解。给出了解析形式的垂深增量公式，利用约束方程组中的垂深方程，将3个独立未知数中的一个未知数表示成其他2个未知数的函数，并用之对设计约束方程组进行降维处理。剖析了隐含未知数的计算细节，给出了隐含未知数的递推算法。提出了降维后的约束方程组的数值求解算法——缩半网格法，该算法可以快速、可靠地求出设计问题的数值解，适用于在开发计算机软件时编程实现。

钻井工程;大位移井;轨道设计;侧位抛物线;方位漂移;数值求解

0 引言

由于地层倾角、岩石和钻头各向异性等因素的综合作用，在实钻井眼轨迹普遍存在方位漂移现象。特别是在高陡构造条件下使用牙轮钻头旋转钻进时，方位漂移问题更为突出。大多数的方位漂移为右首漂移，也有左漂的情况［1］。

如果在进行井眼轨道设计时就充分考虑方位漂移特性，可以在实钻时减少扭方位操作和起下钻次数，进而减少井眼轨道控制的难度和工作量。

刘修善［2］最近提出了考虑方位漂移的三维悬链线轨道设计问题，将经典的二维悬链线大位移井轨道设计推广到了三维的情况，建立了数学模型和数值求解的基本思路，为方位漂移轨道设计技术在实际工作中的应用提供了理论框架。

本文对侧位抛物线型的三维方位漂移轨道设计问题进行了研究，着重阐述了设计约束方程组的求解方法，详细讨论了可以计算机编程实现的数值算法的技术细节。

约定:除非特别声明，文中具有长度量纲的参数其单位为m，角度的单位为rad，井眼曲率和角度变化率的单位为rad/m。

1 设计基础

设计井眼轨道由连续光滑的多段空间曲线构成，每个分段空间曲线称为设计井段。

侧位抛物线轨道由4个设计井段构成:直井段，圆弧过渡段，侧位抛物线段，稳斜段。

方位漂移轨道设计的做法是先在垂直剖面图上进行设计，规定每个设计井段的井斜角变化规律，然后再结合方位变化率进行空间轨迹设计。

1.1 井斜角函数

在每个设计井段上，井斜角随着井深而变化的规律是相同的，可以用下面的井斜角函数来表示:式中:α——设计井段上任意点处的井斜角;ΔL——井深增量，ΔL=L－Lb;L——设计井段上任意点处的井深;Lb——开始点处的井深。

直井段和稳斜段:

式中:αb——设计井段开始点处的井斜角。圆弧过渡段:

式中:kα——造斜率。

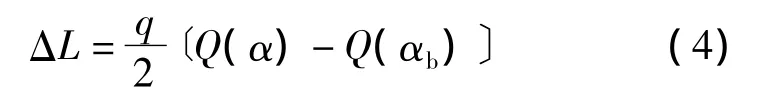
1.2 井斜单元

在设计轨道上任取一连续曲线段，称之为井段。本文用设计井段和井段来区分设计轨道上具有不同属性的连续曲线段。

设计井段上的任一井段称为一个井斜单元［2］。

井斜单元小于或者等于、但不大于某个设计井段;一个设计井段可能划分为多个井斜单元。

下面的情况决不会出现:某个井斜单元的上端点在一个设计井段内部，而下端点在另一个设计井段内部。

1.3 方位单元

将从井口到靶点的垂深划分为连续的m个区间，每个区间称为垂深区间，在每个垂深区间上给定方位变化率的数值。

按照垂深与井深的对应关系，每个垂深区间对应于设计轨迹上的一井段，该井段上的方位角变化规律如下:

式中:φ——井段上任意点处的方位角;φb——井段开始点处的方位角;kφ——方位变化率。

具有上述性质的井段称为设计轨迹上的一个方位单元，简称方位单元［2］。

1.4 计算单元

式中:q——侧位抛物线特征参数，m。

函数Q(x)定义如下:

对于方位单元可能会出现下面的情况:上端点在一个设计井段内部，而下端点在另一个设计井段内部。

为了避免出现这种情况，可以将方位单元再划分成多个更小的井段，使得每个井段都是一个井斜单元。

这种既是井斜单元又是方位单元的井段称为计算单元。在文献［2］中也称为细分单元等。但本文认为“细分”这个词的语义不甚明晰，由于在漂移轨道设计时是以这样的井段为最小划分单元的，本文认为称之为计算单元更言简意赅。

2 设计约束方程组

假设整个设计轨迹可以划分为n个计算单元，则可以给出下面的设计约束方程组［2］:

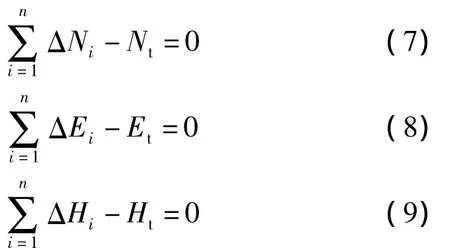
式中:ΔNi、ΔEi、ΔHi——分别为第i个计算单元的北坐标增量、东坐标增量、垂深增量;Nt、Et、Ht——分别为靶点的北坐标、东坐标、垂深。

已知参数包括:造斜点深度，圆弧过渡段造斜率，侧位抛物线段初始井斜角，稳斜段井斜角;垂深区间及方位变化率。

求解设计参数:定向方位角，侧位抛物线特征参数，稳斜段的段长。

2.1 坐标增量计算

计算公式如下:

式中:Li－1、Li——分别为第i个计算单元的开始井深和结束井深;ΔSi——水平投影长度增量。

式(10)～(11)中的定积分无法写成封闭的形式，在计算时只能使用数值积分法［4］。

2.2 独立未知数与隐含未知数

方程组(7)～(9)只有3个方程组，理论上可以求出3个未知数，要求这些未知数之间是独立的。

另外可以看到，在完成设计约束方程组求解之前，某些井深单元的端点井深或井斜角等参数是未知的，例如侧位抛物线段上的井深单元。这些未知数也需要在求解过程中确定出来，但是他们都可以根据已知设计参数或者独立未知数计算出来，称之为隐含未知数。

3 垂深增量公式

在坐标增量公式中，垂深增量公式(12)具有比较特殊的意义，不仅在于积分函数只与井斜角有关、从而有可能求出积分的原函数，而且方位单元是根据已知垂深来确定的，利用垂深已知性可以确定出井深单元的其他参数来。

3.1 显式公式

将式(2)～(4)代入式(12)得:直井段和稳斜段:

圆弧过渡段:

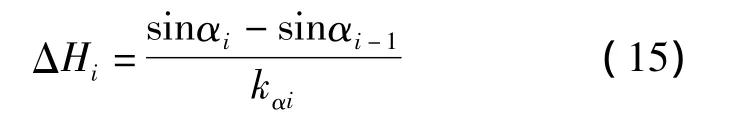
侧位抛物线段:

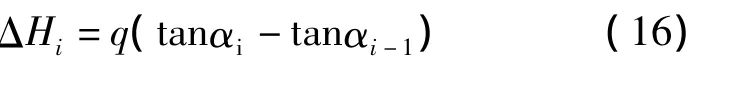
3.2 推论

如果知道一个井深单元的上端点的井深和井斜角，则可以计算出下端点的井深和井斜角以及段长。

例如，假设造斜率或者曲线特征参数为已知数，则从式(15)～(16)可以先求出井斜角αi，再代入式(3)～(4)求出段长ΔLi和井深Li。

而对于稳斜单元，可以直接从式(14)求出这些参数。

3.3 用于降维处理

如果能将要求解的某个独立未知数用其他的独立未知数来表示，则可以将求解三元非线性方程组问题简化成求解二元非线性方程组问题。未知数的减少可以降低方程组的求解复杂度，提高计算速度。

对整个设计轨迹列出垂深方程如下:

式中:Hz——造斜点垂深;αt、Δl——分别为稳斜段的井斜角和段长。

从式(17)解得:

可见，稳斜段长Δl可以从式(8)直接计算出来，求解设计约束方程组时只需要使用前2个方程(7)～(8)即可。

如果用均匀网格法来求解方程组，初始网格点个数为:

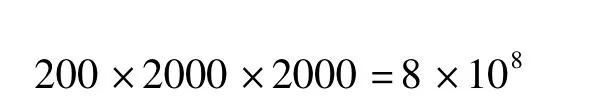
当稳斜段长不作为独立未知数时，初始网格点个数减少为:

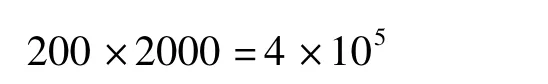
即求解的空间规模降低了3个数量级，求解难度获得降低。

4 求解方程组

记方程(7)～(9)的左端分别为F1、F2和F3，无论使用哪种数值算法求解该方程组，都需要反复计算这3个值。

4.1 隐含未知数的递推计算

用{hr|r=0，1，…，m}表示方位单元的端点垂深序列(已知设计参数)，h0=0，hm=Hz。第r个方位单元上的方位变化率kr为已知设计参数。

用Ω={Hi|i=0，1，…，n}表示最终得到的计算单元的端点垂深序列，H0=0，Hn=Hz。第i个计算单元上的方位变化率Ki待确定。

对于设计轨迹上的第j个设计井段，假设已知其上端点处的井深L(j)0、垂深H(j)0、井斜角α(j)0，则其他已知参数会出现3种情况:

(1)已知设计井段的垂深增量ΔH(j)，例如直井段。在方位单元垂深序列中查找2个下标号r1和r2，使得下式成立:

(2)已知设计井段下端点处的井斜角α(j)1，例如圆弧过渡段、侧位抛物线段等。根据式(15)～(16)可以求出垂深增量ΔH(j)。求出垂深增量ΔH(j)之后，归结为第(1)种情况。

(3)已知设计井段的段长ΔL(j)，例如稳斜段。使用式(1)计算设计井段下端点处的井斜角α(j)1，然后归结为第(2)种情况。

在完成上面步骤之后，该设计井段被分解成多个计算单元，并且每个计算单元端点处的井深、井斜角、垂深、方位变化率等关键参数都已经确定。

进一步，用式(6)计算计算单元端点处的方位角;用式(10)～(11)或者其等价的显式表示式来计算计算单元的北坐标增量、东坐标增量、北坐标、东坐标等等。

完成第j个设计井段的计算单元划分和井身参数计算之后，继续对第j+1个设计井段执行同样的操作，直到最后一个设计井段。

上述递推过程完成之后，得到F1、F2和F3的确定值。

4.2 设计约束方程组的数值求解

经过降维处理之后的设计约束方程组(7)～(8)为二元非线性方程组，没有解析解，需要使用数值算法求数值解(近似解)。求解非线性方程组的数值算法有很多种［5，6］，大部分算法需要使用导数信息，并且迭代初始值对算法的收敛性有较大影响，如果迭代初始值选择不当，则迭代过程可能不收敛、或者收敛速度很慢，在方程组有多个解的情况下，还有可能收敛到伪解。

算法研制的最终目的是为钻井设计人员(用户)提供一套可靠性好的计算机软件，用户在使用该软件时，只需要给定必要的设计参数、不必设置太多的算法控制参数就能够快速求出轨道设计问题的解来。本着这一原则，下面给出一个具体的迭代算法——缩半网格法。

记x、y、z为方程组(7)～(9)的3个独立未知数:定向方位角、侧位抛物线特征参数、稳斜段的段长。方程左端项分别记为F1(x，y，z)、F2(x，y，z)和F3(x，y，z)，前面已经说明从垂深增量方程可以将某个参数z表示为其他2个参数的函数〔见式(18)〕:

对每个网格点(xi，yj)，利用垂深方程求出对应的第3个待定参数zij=λ(xi，yi)，然后使用第4.1节中的方法求出全部的隐含未知数并得到方程左端项的值，再代入式(22)求出网格点函数值Fij。

求出所有的网格点函数值中的最小的函数值，对应的网格点为(x(0)，y(0))，以该网格点为矩形中心将初始矩形缩小一半，得到新的约束矩形:

用新的约束矩形重复上述计算过程，直到约束矩形的边长或者最小函数值小于给定的允许误差时停止迭代过程。

5 结论

(1)通过垂深方程可以将3个独立未知数中的一个表示为其他未知数的函数，从而使得设计约束方程组可以降维为二元非线性方程组，降低了数值求解的规模和难度。

(2)结合隐含未知数的递推计算策略，缩半网格法能够可靠地求出降维后的设计约束方程组的数值解，特别适用于计算机编程实现。

［1］刘修善.井眼轨道几何学［M］.北京:石油工业出版社，2006.

［2］刘修善.三维悬链线轨道的设计方法［J］.石油钻采工艺，2010，32(6):7－10.

［3］鲁港，余雷，杨文举.大位移井抛物线剖面设计的数值计算［J］.石油地质与工程，2009，23(5):81－83.

［4］施吉林，刘淑珍，陈桂芝.计算机数值方法［M］.北京:高等教育出版社，1999.

［5］李庆扬，莫孜中，祁力群.非线性方程组的数值解法［M］.北京:科学出版社，1987:38－119.

［6］王德人.非线性方程组解法与最优化方法［M］.北京:高等教育出版社，1979:28－113.

Numerical Algorithm for the Design of 3D Lateral Parabola Azimuth Drift Well-path

LU Gang1，XIA Bo-yi2(1.Exploration＆Development Research Institute，Liaohe Oilfield Company，PetroChina，Panjin Liaoning 124010，China;2.Engineering＆Technology Research Institute，Great Wall Drilling Corporation，PetroChina，Panjin Liaoning 124010，China)

The design constrained equations of azimuth drift is a nonlinear one that contains 3 independent and several hidden unknowns，the numerical iteration method should be used to get the numerical solution.The vertical depth increasing equation was provided，by using vertical depth increasing equation of the constrained equations，one of the 3 independent unknowns was expressed as functions of the other 2 unknowns，which were used for dimension reduction of the design constraint equations.The paper analyzed the calculation details of hidden unknowns and gave the recursive algorithm for hidden unknowns.The numerical value arithmetic of constrained equations after dimension reduction was also put forward，that was half-shrinkage grid method，which could be applied to quickly and reliably find the numerical solutions of design，especially for programming computer software.

well drilling engineering;extended reach well;well-path design;lateral parabola;azimuth drift;numerical algorithm

TE243

A

1672－7428(2012)06－0023－04

2011－12－11

国家科技重大专项“大型油气田及煤层气开发”之课题21－6“钻井工程设计和工艺软件”(2008ZX05021－006)和中国石油长城钻探工程有限公司科技开发项目“钻井数据管理系统配套与应用”(2010A11)资助

鲁港(1963－)，男(汉族)，辽宁锦州人，中国石油辽河油田公司勘探开发研究院高级工程师，钻井工程专业，硕士，从事石油钻探领域数学模型及算法的理论研究和计算机软件开发工作，辽宁省盘锦市兴隆台区石油大街95号，214811882@qq.com。