基于GRA-DEA混合模型的沿海地区海洋经济效率分析与评价

赵 昕，郭恺莹

（中国海洋大学经济学院，山东 青岛 266100）

引 言

海洋是人类生存与发展的资源宝库和重要空间，是具有重要战略意义的开发领域。开发海洋资源、发展海洋经济已成为世界各沿海国家实现可持续发展的重要举措。中国海洋经济较世界海洋经济发展滞后大约10年，但随着海洋资源开发的深入，海洋产业已成为中国国民经济发展新的增长点并显示出了巨大的发展潜力，海洋经济对沿海地区的发展产生了举足轻重的战略影响。据初步核算，2011年全国海洋生产总值45 570亿元，比上年增长10.4%，海洋生产总值占国内生产总值的9.7%。其中，海洋产业增加值26 508亿元，海洋相关产业增加值19 062亿元。

海洋经济效率作为衡量海洋经济投入产出的指标之一，是指以现有的海洋环境资源为基础，在开发利用海洋资源的过程中，投入人力、物力、财力基础上所能获得的经济收益。它既决定于劳动生产率，更决定于该生产率究竟能产生多少价值。因此，正确衡量各地区的海洋经济效率，不仅可以评判各地区投入产出情况，也可以为各地区的海洋产业投入指导方向。

本文正是基于各沿海地区的海洋经济发展情况，对各地区的海洋经济投入产出情况进行分析和研究。首先根据影响海洋经济的主要因素，提出了衡量各沿海地区海洋经济效率的指标体系，然后运用常用的灰色关联方法找出主要指标，最后在主要指标的基础上，运用数据包络分析方法，得到各沿海地区的投入产出情况。

1 GRA-DEA混合模型

海洋经济效率的评价一般采用投入—产出模型和数据包络分析模型进行分析，前者通过大量的数据搜集和分类整理，整理出较为全面的投入—产出表，通过该表得到相应的经济效率；而后者是以“相对效率”为基础，根据多指标投入和多指标产出对相同类型的单位或部门进行相对有效性或效益评价的一种新的系统分析方法，该种方法评价的依据是决策单元的“输入数据”和“输出数据”。“输入数据”是指决策单元在某种生产活动中所消耗的某些量，例如投入的资金总额、投入的劳力总数、占地面积等（即“生产要素”的投入）；“输出数据”是指决策单元经过一定的投入之后，产生的表明该种活动成效的某些量，例如各种类型产品的数量、产品的质量、经济效益等。根据输入数据和输出数据来评价决策单元的效率，即所谓评价决策单元之间的相对有效性。

本文所采用的经济效率的评价方法是对数据包络分析方法的一个改进，主要是对输入数据及输出数据选取的改进，建立GRA-DEA混合模型。首先通过引入关联度分析方法对评价体系中进行主要指标提取，在此基础上运用数据包络分析方法进行经济效率评价。

1.1 GRA分析方法

灰色关联度（GRA）分析方法的提出，是为了通过该种方法理清系统中各因素间的主要关系，找出影响最大的因素，把握矛盾的主要方面。所谓关联度是指对两个系统或两个因素之间关联性大小的量度，它描述系统发展过程中因素间相对变化的情况，即变化大小、方向及速度等指标的相对性。如果两者在系统发展过程中相对变化基本一致，则认为两者关联度大；反之，两者关联度就小。灰色关联度分析方法的计算步骤如下：

首先是对原始数据的变换。由于系统中各因素的量纲（或单位）不一定相同，这样的数据很难直接进行比较，且它们的几何曲线比例也不同，因此，对原始数据需要消除量纲（或单位），转换为可比较的数据序列。转换方法有：均值化变换、初值化变换和标准化变换。均值化变换是指先分别求出各个序列的平均值，再用平均值去除对应序列中的各个原始数据，所得到新的数据列即为均值化序列。初值化变换是指分别用同一序列的第一个数据去除后面的各个原始数据，得到新的倍数数列即为初值化数列。标准化交换是指先分别求出各个序列的平均值和标准差，然后将各个原始数据减去平均值后再除以标准差，这样得到的新数据序列即为标准化序列。

其次是计算关联系数。经数据变换的母序列记为{X0（t）}，子序列记为{Xi（t）}，则在时刻t=k时母序列{X0（t）}与子序列{Xi（t）}的关联系数（LOi（k））可由下式计算：

式中：ΔOi（k）表示k时刻两比较序列的绝对差，即ΔOi（k）=|x0（k）-xi（k）|，其中1≤i≤m；Δmax和Δmin分别表示所有比较序列各个时刻绝对差中的最大值与最小值。因为比较序列相交，故一般取Δmin=0；ρ称为分辨系数，其意义是削弱最大绝对差数值太大引起的失真，提高关联系数之间的差异显著性，ρ∈（0，1），一般情况下可取 0.1～0.5。

再次是求关联度。由以上所述可知，关联度分析实质上是对时间序列数据进行几何关系比较，若两序列在各个时刻点都重合在一起，即关联系数均等于1，则两序列的关联度也必等于1。另一方面，两比较序列在任何时刻也不可垂直，所以关联系数均大于0，故关联度也都大于0。因此，两序列的关联度便以两比较序列各个时刻的关联系数的平均值计算，即：

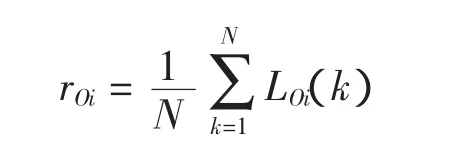
式中：rOi为子序列i与母序列0的关联度，N为比较序列的长度。

最后是排关联序和列关联矩阵。将m个子序列对同一母序列的关联度按大小顺序排列起来，便组成关联序，记为{X}。它直接反映各个子序列对于母序列的优劣关系。关联矩阵是对各时序序列关联度进行矩阵排列。关联序和关联矩阵是进行决策的依据。

1.2 数据包络分析

数据包络分析方法（DEA）的基础是决策单元的确定。一个经济系统或一个生产过程可以看成是一个单元在一定的可能时间范围内，通过投入一定数量的生产要素并产生一定数量的产品的活动，虽然这种活动的具体内容各不相同，但其目的都是使该项活动取得最大效益。由于产出是决策的结果，所以这样的单元被称为决策单元（DMU）。在DEA方法中，使用较多的是同类型的DMU，而选取相同的DMU，是指具有以下三个特征的决策单元：一是具有相同的目标和任务；二是具有相同的外部环境；三是具有相同的输入和输出指标。

设某个DMU在一项经济活动中的输入向量为 x=（x1，x2，…，xm）T，输出向量为 y=（y1，y2，…，ys）T，于是可以简单的用（x，y）来表示这个DMU的整个生产活动。称集T={（x，y）|产出y能用输入x生产出来}为所有可能的生产活动构成的生产可能集，一般假设生产可能集满足下面四条公理，即凸性、锥性、无效性和最小性。迄今为止，最具代表性的经典DEA模型有：C2R模型、BC2模型以及由学者（R.Fare and S.Grosskopf）给出的FG模型和由学者（L M Seiford and R M Thrall）给出的ST模型。本文仅针对前两种模型进行介绍和应用。

1）C2R模型

C2R模型是由A Charnes等人以单输入单输出的工程效率概念为基础提出的，它是第一个DEA模型，它讨论的是具有有限多个决策单元，相应的生产可能集为闭凸锥的情况，在该模型下的有效性对应的决策单元既是规模有效又是技术有效的。

设有 n 个决策单元 DMUj，j=1，2，…n。每个决策单元都有m种“输入”（表示该决策单元对“资源”的耗费），以及s种“输出”（表示该决策单元消耗了“资源”之后，表示“成效”的数量），这里DMUj的输入为Xj=（x1j，x2j……xmj）T，输出为Yj=（y1j，y2j……ysj）T。基于输入的评价DMU总体效率的具有非阿基米德无穷小的C2R模型如（Ⅰ）所示：

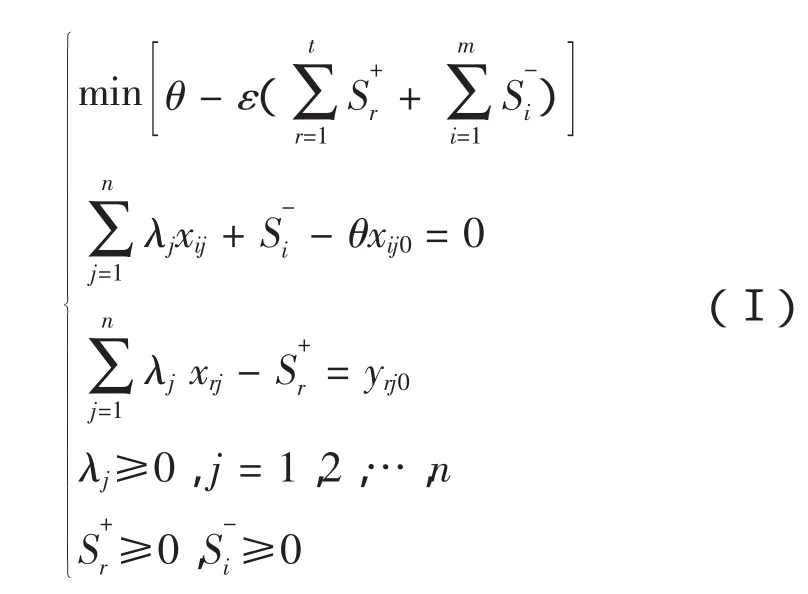
在模型（Ⅰ）中，xij为第j个决策单元对第i种类型投入的投入量，yrj为第j个决策单元对第r种类型产出的产出量，与分别为松弛变量和生育变量，也称为投入冗余和产出不足，ε为一非阿基米德无穷小量，可取（ε=10-）6，λj、、、θ为待估计参量。

C2R模型可以评价DMU的总体效率，即技术和规模的综合效率。因此，可以根据DEA的相关软件进行分析得到的一些数值来对某些现象进行经济学解释。

①当θ=1时，决策单元DMU为DEA有效。

②当θ＜1时，决策单元DMU为DEA无效。

④若存在λj（j=1，2，…，m），使成立，则DMUj为规模效率不变，即规模有效；若＜1，则DMUj为规模效率递增；若，则DMUj为规模效率递减，且的值越大，规模递减趋势越大。

2）BC2模型

同样作为DEA模型，BC2模型也是研究各个决策单元有效性的问题，但与C2R模型不同的是，BC2模型不考虑生产可能集满足锥形条件，同时BC2模型可以分别评价DMU的技术效率和规模效率。

设有 n 个决策单元 DMUj，j=1，2，…，n。每个决策单元都有m种“输入”（表示该决策单元对“资源”的耗费），以及s种“输出”（表示该决策单元消耗了“资源”之后，表示“成效”的数量），这里 DMUj的输入为 Xj=（x1j，x2j……xmj）T，输出为Yj=（y1j，y2j……ysj）T。基于输入的评价DMU纯技术效率的具有非阿基米德无穷小的BC2模型如（Ⅱ）所示。

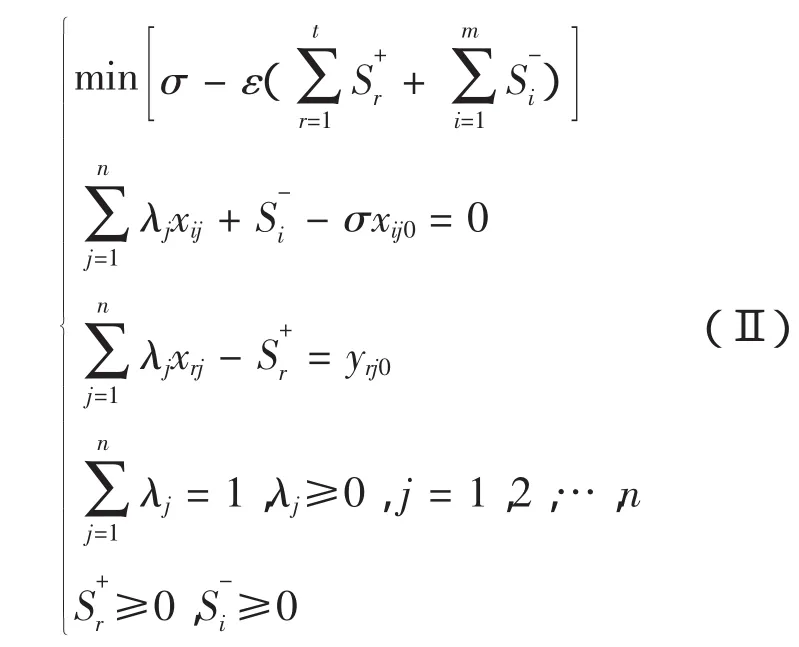
该模型计算的是DMU的纯技术效率。若σ=1，则DMU，为DEA有效。设总体效率为θ，纯技术效率为σ，纯规模效率为s，则DMU的纯规模效率的计算公式为s=θ/σ。

2 沿海地区海洋经济效率的实证分析

2.1 指标的确定

由于中国海岸线较长，各个沿海地区的海洋产业类型差异较大，但是各沿海地区海洋经济的影响因素不尽相同。因此在评价体系中，分别从人力资源、科技投入、海洋贡献度、资产投资、环境损耗和对外开放程度6个方面参与评价。针对上述6个方面，选取相应经济指标进行分析，包括8项输入指标和1项输出指标。输入指标包括涉海就业人数（X1）、科研人员（X2）、港口货物吞吐量（X3）、海洋捕捞量（X4）、海水养殖量（X5）、固定资产投资（X6）、废水入海量（X7）和接待入境旅游人数（X8）。而输出指标则选取海洋生产总值（Y）来反映各沿海地区的海洋经济产出情况。

2.2 样本数据选取

考虑到数据的可得性，本文依据《沿海行政区域分类与代码》（HY/T 094-2006）对各地区的海洋经济投入产出情况进行实证分析。根据《中国海洋统计年鉴2010》，搜集中国沿海地区（包括辽宁、天津、河北、山东、上海、江苏、浙江、福建、广东、广西、海南）2009年相应统计数据作为输入和输出指标数值，并利用相关DPS和DEAP分析软件进行实证研究。

2.3 GRA-DEA混合模型分析

确定评价指标后，由于输入指标较多且相关程度相差较大，因此有必要对这些指标进行筛选，提取主要指标，本文采用灰色关联度分析对主要指标进行提取。

对于较稳定的社会经济系统数列作关联度分析时，对原始数据的处理多采用均值化变换，因此本文选择均值化变换对原始数据进行处理。运行DPS分析软件，选择数据转换方式为均值化变换、分辨系数取0.1，参数Δmin取0。最后系统输出分析结果，包括数据转换结果、母序列与其他子序列的绝对差值、最大差值Δmax、关联系数、关联序及其关联矩阵等。

根据软件运行的结果，Y与其他因子的关联系数如表1所示。

表1 Y和其它因子的关联序Tab.1 The relational ordinal between Y and other factors

从上表中可以看出，在指标体系中，X3、X2、X1、X8与Y的关联度较大，因此在接下来的数据包络分析中选择这四个指标作为输入单元。

将11个沿海城市2009年的海洋经济输入指标和输出指标的相关数据代入C2R与BC2模型中，得出海洋经济运行的相对效率，如表2所示。

从软件运行结果可以得出：

（1）天津、河北、上海、江苏、福建和山东六个沿海地区海洋经济的综合效率θ=1，为DEA有效；剩余的五个省市地区的综合效率θ＜1，为DEA无效。

（2）天津、河北、上海、江苏、福建和山东海洋经济发展的σ值和s值都为1，即同时为纯技术有效和纯规模有效，说明这六个沿海地区与其他五个沿海地区相比，海洋经济发展具有相对优越性，投入资源的组合结构相对合理。在投入产出技术效率方面，不存在投入冗余和产出不足的情况；在规模效益方面，处于最佳状态，因此同时为技术有效和规模有效。

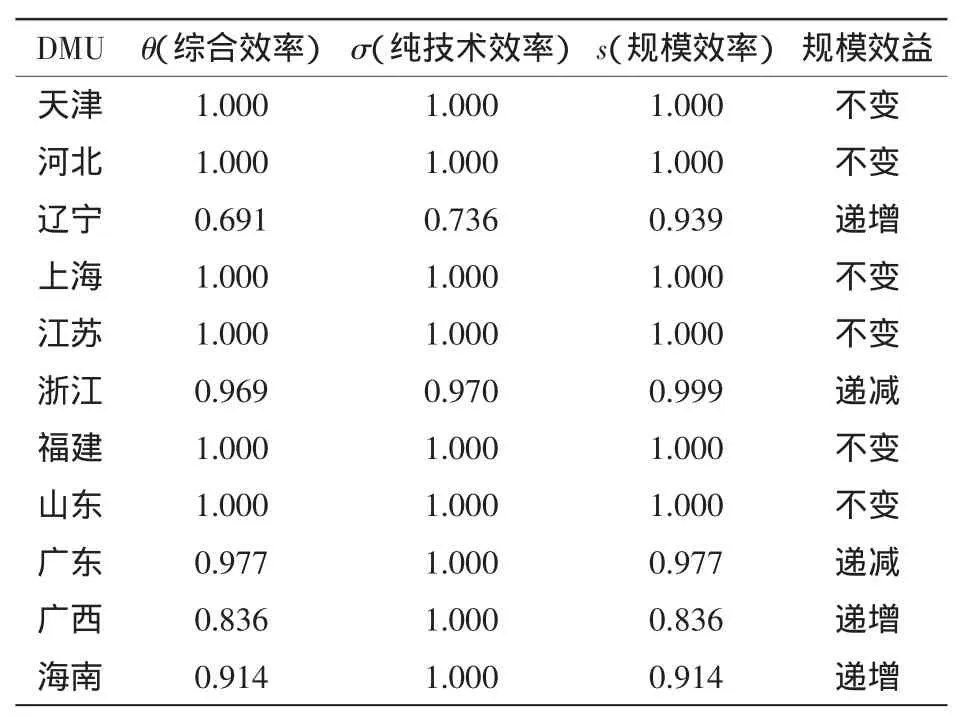
表2 中国沿海地区2009年海洋经济相对效率Tab.2 The relative efficiency of marine economy in coastal areas in 2009

（3）DEA无效的沿海地区中的广东、广西、海南的σ=1，为纯技术有效；辽宁、浙江的σ＜1，为纯技术无效。由此可见，广东、广西和海南的DEA无效是由纯规模无效引起的，而辽宁省和浙江省的DEA无效是由纯技术无效和纯规模无效共同作用造成的。因此，辽宁和浙江在以后的海洋经济发展中应当整合资源技术，逐步实现资源配置的最优组合，提高资源利用效率，并适当扩大海洋经济规模。

（4）DEA无效的各沿海地区除广东省和浙江省以外，都处于规模效益递增阶段，这些地区海洋经济纯规模无效率的原因是海洋经济规模没有达到合理的程度，因此需要投入更多的资源扩大海洋经济规模，达到规模经济。而对广东省和浙江省来说，海洋经济纯规模无效率的原因是海洋经济规模超过了合理的水平，因此需要合理的分配资源，避免资源的浪费，使海洋经济达到规模效应。

（5）由纯技术无效和纯规模无效共同作用的DEA无效的辽宁省和浙江省，均存在投入冗余的情况。对于辽宁省而言，若要使资源合理分配，可在现有基础上X1减少80.456万人，X2减少479.51人、X3减少14 615.144万t和X8减少446 660.741人。而对于浙江省，同样为了避免资源浪费，可在现有基础上X1减少12.094万人，X2减少42.857人、X3减少2 172.245万t和X8减少143 852.142人。

4 结 论

本文以各沿海地区海洋经济效率为研究对象，采用GRA-DEA混合模型对海洋经济投入产出情况进行分析。在这一过程中主要得出以下结论：

（1）由于海洋经济效率的影响因素较多，在分析经济效率时需要建立一个比较全面的指标体系，但是在做具体的分析时，需要提取主要因素，忽略次要因素的影响。同时海洋产业作为典型的灰色系统，不宜采用统计学中的因子分析法，因此本文采用灰色系统理论中的关联度分析对中国海洋经济效率进行分析，得到影响海洋经济效率的主要因素有涉海就业人数、科研人员数目、港口货物吞吐量和接待入境旅游人数。

（2）通过对海洋经济投入产出的数据包络分析，可以看到部分地区目前呈现海洋经济效率良好的态势，但是部分地区由于资源整合或规模效应的问题导致海洋经济效率低下，影响该地区的海洋生产总值。因此，针对这部分地区，应合理整合海洋资源，适度调整相关海洋产业规模，以实现海洋资源的有效利用。

[1] 唐启义，冯明光.DPS数据处理系统——实验设计、统计分析及模型优化[M].北京：科学出版社，2006.

[2] 付静，周厚诚，李萍.基于灰色系统理论的广东省海洋经济关联度分析[J].海洋开发与管理，2009（2）：89-92.

[3] 冯俊文.基于数据包络分析的标杆管理理论与应用研究[D].南京：南京理工大学，2010.

[4] 柳顺，杜树新.基于数据包络分析的模糊综合评价方法[J].模糊系统与数学，2010（2）：93-98.

[5] Charles S Colgan，何广顺，王晓慧，等.海洋经济和沿海经济的计量理论和方法[J].经济资料译丛，2010（2）：59-74.

[6] Francisco J.Andre′，Ine′s Herrero，Laura Riesgo.A modified DEA model to estimate the importance of objectives with an application to agricultural economics [J].Empirical Research in the EU Banking Sector and the Financial Crisis,2010（5）：371-382.