冲击作用下岩石破碎比功理论分析及模糊预测模型

曹 钧，沈志康，胡永乐，范成洲，王定贤，邓丽蓉，杨 欢

（西北核技术研究所，西安 710024）

1 引 言

用冲击方式破碎岩石，在采矿、冶金、水利、市政工程及国防工业等领域的工程实践中应用十分普遍[1]，这种方式破碎岩石量大、速度快，靠冲击力的冲击压碎作用，达到破碎岩石的目的[2－3]。岩石破碎比功是研究冲击方式破碎岩石的主要性能参数之一，主要确定工程作业的性能参数，评估破岩机具的性能。岩石破碎比功是指破碎单位体积岩石所需的能量，在破碎等量岩石的情况下，比功小就意味着破岩机具的效费比高。随着科学技术的发展，工程实践中要求通过评估破岩机具性能，实现对工程工期和费用准确预估，而破岩机具性能评估误差会导致工程延误，预算超支。破岩机具性能主要评估手段主要是对其破岩能力、进尺速率以及设备利用率等进行评估。有许多预测岩石破碎比功值的模型，也有用线性试验装置直接测量的[4－5]。本文从岩石破碎机制分析出发，通过建立岩石破碎比功模态，确定破岩机具结构尺寸、岩石力学特性和破岩工艺三类对岩石破碎比功有影响的参数。引入模糊逻辑法，将上述参数作为模糊逻辑分析的输入变量，建立一种基于人工智能模糊逻辑模型来预测岩石破碎比功值的新方法。

2 岩石破碎机制分析及其比功模态的建立

2.1 岩石破碎机制分析

在冲击力作用下，设分布在破岩机具上的作用力为P (见图1)，而岩石的抗压入强度为σ压，其碎岩过程分如下几个阶段，（1）弹性变形阶：当 P＜0.4σ压，形成压力面，边缘产生裂隙，当P力撤除，岩石面恢复原状，裂隙消失。（2）压力压皱阶段：当P = (0.4～0.6)σ压，裂隙延伸，出现主压力体，称之为疲劳阶段（表面裂隙不再消失），岩石产生表面破碎。（3）破碎阶段：当 P≥0.6σ压时，自岩石表面出现裂隙,形成剪切体，随着P的增加，剪切体开始向外崩落，主压力体被压碎，形成破碎坑。当破岩机具与岩石接触所产生的接触压力等于或大于岩石的极限强度（或压入硬度），则岩石产生跃进式破碎，破碎块度大，破碎速度比研磨区大得多，并随冲击力的增加而增加。该阶段破碎岩石量大、速度快，机具磨损小，岩石破碎过程所消耗的比功亦小，正是破岩所追求的目标[6]。

图1 岩石破碎断面Fig.1 The section of broken rock

2.2 岩石破碎比功模态建立

根据能量守恒原则，破岩机具所作的功应该包含破碎岩石、转化为热能以及形成振动波等所消耗的能量，而岩石破碎所消耗的能量是破岩机具所做的功的主要部分。为简化分析，将岩石破碎所消耗的能量看作为破岩机具所做的功，可列方程[7－9]：

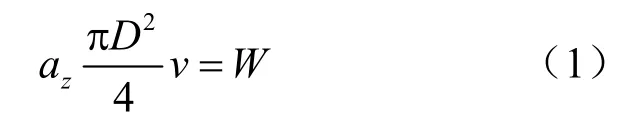
式中：az为岩石破碎比功(kW · h/m3)；D为破岩断面直径（m）；v为掘进速度（m/h）；W为破岩机具所作的功（kW）。

令

则式（1）可简化为

为了分析破岩机具的主要性能参数与破碎岩石比功az的关系，作以下假设：（1）岩石为一均质弹性体；（2）将破岩机具与岩石面垂直接触简化为一个集中力点；（3）将破岩机具作业面简化为半无限体界面模型。

按弹性理论分析岩石的应力状态。破岩机具作用于半无限体的应力状态模型如图2所示。

图2 破岩机具作用下岩石单元体应力状态模型Fig.2 Stress mode of the rock unit under acting forces of tools

冲击力 Pz引起的岩石诸应力分量为

式中：μ为泊松比；R、z、r为圆柱坐标。

当轴向应力σz＞σucs(σucs为岩石抗压强度极限）时，岩石即从整体上破碎下来。将σz=σucs代入式（4）中第三式，解出平行于边界岩石破碎半径r为

令r = 0，代入式（5），得到破碎深度z0为

由式（5）、（6）可得破碎岩石体积：

大量研究资料表明，由于冲击破岩是既有冲击压碎、又有剪切破碎作用的复合运动，这就给刀齿侵入岩石参数的研究，造成极其复杂的困难局面。研究岩石破碎的学者仅能对岩石破碎前的应力状态有较明确的观点和论述，而对裂纹的发生、扩展、汇交、破碎判据、漏斗形成等一系列问题仍处于实验研究、现象积累和观点争鸣阶段[5－6]。前苏联斯科琴斯基矿业研究院对于不同形状的破岩机具压入岩石的应力状态和破碎岩石机制进行了研究。以布希涅希克的理论为基础，假定破岩机具是绝对刚体，接触表面没有摩擦，外载荷垂直于作用面。对于圆柱体、球形、抛物线形和圆锥形的的破岩机具进行了研究，结果见表 1。表中，P为作用于机具齿上的外载荷；P0为接触面的平均压力；h为机具齿压入岩石的深度；Zk为产生最大剪应力的深度，即τ=τmax时的临界深度；τ为岩石的剪应力；μ为泊松比；m=1/μ；A=8/k3；k=D/；D = 2R；H为机具齿高度；a为接触面积等效半径；α为圆锥形齿的锥角；G为剪切模量；r、Z为圆柱坐标。根据研究者的意见，在其他条件相同时，抛物线形比球形可承受较高的剪应力，更适合应用于坚硬的岩石[5－10]。

通过上述对岩石破碎比功模态的分析可以看出，岩石破碎比功主要与机具破岩工艺参数和几何参数及岩石的力学参数有关。在分析岩石破碎比功与上述参数之间的关系时，虽然作了简化和理想化的假设，但还是很难给出一个综合的表达式。其实，在岩石破碎比功模态中，存在大量非线性、不确定的问题。而模糊数学的诞生，为解决上述问题开辟了一条新的途径。

3 岩石破碎比功模糊预测模型建立

3.1 确定输入输出变量

根据上述对岩石破碎比功模态的分析，确定预测模型的输入变量有破岩机具所作的冲击功，主要考虑冲击力、冲击速度、冲击力矩以及机具旋转速度等冲击工艺参数，破岩机具结构参数主要考虑机具齿的高度，接触岩石面积等效半径等；岩石力学参数主要考虑岩石单轴抗压强度、岩石剪切应力、岩石可钻性等，输出变量为岩石破碎比功。图3为利用 MATLAB建立的输入输出变量模糊逻辑推理模型[11]。

表1 几种常见形状的破岩机具冲击侵入岩石参数[5]Table1 Penetration parameters of several tools

图3 岩石破碎比功模糊逻辑推理模型Fig.3 The fuzzy logical inference model of specific power of broken hard rock

3.2 模糊逻辑推理规则

要进行模糊推理运算，一般采用以模糊条件语句描述的一组模糊控制规则：

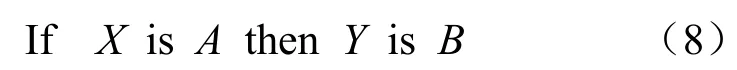
式中：A、B分别为输入和输出对应论域上的模糊集，它们表征诸如正大、正中、负大等语言变量。用模糊集来描述研究系统的行为特征信息。

4 工程应用实例

4.1 确定输入输出变量基本论域

输入变量的取值依据近50年的钻井实践数据、相关试验数据以及相关手册。冲击力（钻压）P的取值范围为 500～1000 kN，其基本论域为[500，1000]；冲击速度v的取值范围为0.1～1.6 m/s，其基本论域为[0.1，1.6]。钻具转速 n的取值范围为5～12 r/min，其基本论域为[5，12]。冲击力矩M取值范围是50～300 kN·m，基本论域为[50，300]；岩石单轴抗压强度σucs的取值范围是60～ 245 MPa，其基本论域为[60，245]。岩石抗剪切强度τ的取值范围是5～30 MPa，基本论域为[5，30]。接触岩石面积等效半径 a的取值范围为 8～45 mm，其基本论域为[8，45]。机具齿高 H 取值范围为 2.5～30 mm，其基本论域为[2.5，30]。岩石可钻性K的取值范围是 6～11，基本论域为[6，11]。输出变量为岩石破碎比功az，取值范围是0.1～500 kW·h/m3，基本论域为[0.1，500]。

4.2 模糊预测推理运算

模糊推理机设计选择 Mamdani 模型，根据工程实践和知识库，在该模糊推理机总共编写512条模糊逻辑推理规则。图4为该岩石破碎比功模型的MATLAB模糊逻辑推理规则观测窗。将适当的数据输入该模型，就可提供破岩比功水平的估计，取P = 750 kN，ν = 0.9 m/s，n = 8.5 r/min，M = 175 kN · m，σucs= 153 MPa，τ= 17.5 MPa，H = 16.3 mm，a = 24 mm，K = 9，预测到岩石破碎比功为 316 kW·h/m3。

图4 工程实例岩石破碎比功模型的MATLAB模糊逻辑推理规则观测窗Fig.4 Observing window of MATLAB fuzzy logical inference model for the project instance specific power of broken hard rock

4.3 模型所得结果与工程实践中的真实值对比

通过对比相同输入条件下模型所得结果与钻井实践中的真实岩石破碎比功，来考证该模型的实用性，对比情况如图5所示。

图5 模型所得结果与钻井实践中的真实值对比Fig.5 Comparative analysis graphic of simulation values and real values of specific power

从图5可以看出，模型所得结果的图形拟合曲线为y＝0.9x，R-Squared = 0.912，这意味着模型所得结果与钻井实践中的真实岩石破碎比功接近。模型所得结果比钻井实践中的真实岩石破碎比功值略小，这是因为研究模型取得数据范围比较宽泛，特别是对于非常坚硬的岩石，岩石单轴抗压强度和抗剪切强度都非常高，而刀齿侵入岩石深度又非常小（小于2.5 mm），这时该模型就不能够真实反映出岩石破碎比功的实际情况，而于真实岩石破碎比功有一定的偏差。

5 结 语

模糊逻辑法广泛应用于各种研究领域，特别是复杂系统和不确定系统。如果没有一定的假设条件，那么需要考虑影响系统的许多变量来对其进行预测，这一过程相当复杂，而且得到的结果往往很难用于指导实践。模糊模型利用其特有的柔性方法，能够对人类的生产实践经验进行逻辑表达，并通过模糊推理运算，获得比较切合实际的结果，应用于实践预测，可得到较好的应用价值。

本文将模糊逻辑法引入冲击破碎岩石的工程领域，建立了用于预测岩石破碎比功的模型，对于给定破碎岩石机具主要几何尺寸、岩石力学主要特性参数和破碎岩石主要工艺参数的情况下，可有效预测滚刀岩石破碎比功这一工程领域的重要特征参数。通过对比模型所得结果与工程实践中的真实破岩比功，该模型所得结果与工程实践中的真实值比较接近，模型设计合理，模糊推理规则能够表达工程实践。在实际应用该模型时，只要选取合理的输入变量参数值，就可得到与之对应的岩石破碎比功值。利用该模型所得结果，可以实现对工程工期和费用准确预估，并可为破岩机具结构设计以及现场选取破岩工艺参数提供指导。

[1]周兴旺. 我国特殊凿井技术的发展与展望[J]. 煤炭科学技术,2007,34(10): 10－17.ZHOU Xing-wang. Development and out look of mine shaft special sinking technology in China[J]. Coal Science and Technology,2007,34(10): 10－17.

[2]张永成,刘志强. 钻井法凿井技术的发展和展望[J]. 建井技术,2003,24(2): 1－6.ZHANG Yong-cheng,LIU Zhi-qiang. Development and prospect of drilling shaft technology[J]. Mine Construction Technology,2003,24(2): 1－6.

[3]崔广心. 大直径钻井法在地下工程中的应用与研究[J].探矿工程(岩土钻掘工程),2001,45(4): 6－8.CUI Guang-xin. Application of Large diameter drilling inunderground engineering[J]. Exploration Engineering(Rock & Soil Drilling and Tunneling),2001,45(4): 6－8.

[4]曹钧,陈昌明. 大口径钻井钻压设计探讨[J]. 矿山机械,2008,36(7): 8－10.CAO Jun,CHEN Chang-ming. Probing into the bit-pressure design for large-diameter shaft drilling[J].Mining & Processing Equipment,2008,36(7): 8－10.

[5]李夕兵,古德生. 岩石冲击动力学[M]. 长沙: 中南工业大学出版社,1994.

[6]蔡美峰,何满潮,刘东燕,等. 岩石力学与工程[M]. 北京: 科学出版社,2004.

[7]况雨春,伍开松,杨迎新,等. 三牙轮钻头破岩过程计算机仿真模型[J]. 岩土力学,2009,30(增刊1): 235－238.KUANG Yu-chun,WU Kai-song,YANG Ying-xin,et al.Simulation model of drilling process of three-cone bit[J].Rock and Soil Mechanics,2009,30(Supp.1): 235－238.

[8]MISHNAEVSKY L L. Physical mechanisms of hard rock fragmentation under mechanical loading: A review[J].Rock Mech. Min. Sci. & Geomech. Absrt,1995,8: 763－766.

[9]张照煌,叶定海,袁昕. 楔形刃压头作用下岩石力学性能研究[J]. 应用基础与工程科学,2011,19(6): 978－985.ZHANG Zhao-huang,YE Ding-hai,YUAN Xin. A study of rock mechanical properties under the effect of the wedge-shaped blade head[J]. Journal of Basic Science and Engineering,2011,19(6): 978－985.

[10]葛和平,孙岩,朱文斌,等. 岩石破裂行为的实验研究[J]. 高校地质学报,2004,20(2): 290－296.GE He-ping,SUN Yan,ZHU Wen-bin et al. Experiment on the Fracture Behavior in Rocks[J]. Geological Journal of China Universities,2004,20(2): 290－296

[11]韩峻峰,李玉惠. 模糊控制技术[M]. 重庆: 重庆大学出版社,2003.