基于水-岩相互作用的泥岩库岸时变稳定性分析

周世良，刘小强，尚明芳，李 怡

（重庆交通大学 河海学院，重庆 400074）

1 引 言

富宁港位于云南省境内，地处云贵高原向桂东溶原过渡的斜坡地带。在广西百色水利枢纽蓄水后，港区库岸将受到高水位的长期浸泡和水位周期性涨落影响，库岸岩体力学性能和边坡稳定性将具有明显的时变特征。因此，开展水-岩相互作用下岸坡稳定性研究成为库区港口工程建设中亟待解决的关键技术问题。

传统的库岸稳定性分析较多地从水对岸坡的力学效应进行考虑[1－4]。但基于岩土体力学参数劣化的库岸稳定性研究相对较少。张明等[5]利用大型原位推剪试验对比分析了仅考虑水-岩力学作用下、水-岩力学作用及物理化学作用下堆积体的稳定性变化特点，并指出实际工程中仅考虑水-岩力学作用得到的稳定系数误差较大。刘新荣、傅晏等[6－8]以室内岩石力学试验为基础，分析了三峡库区某砂岩边坡在水-岩相互作用下的稳定性。但文中未考虑含有节理裂隙的岩体强度与岩石试样强度之间差别，其计算结果与实际工程存在一定偏差。工程中，库岸在复杂的水文地质条件下，其稳定性不仅受控于水对岸坡的力学作用，同时受控于水对岸坡的物理化学作用。在水-岩相互作用下，客观地分析岩体力学性质的变化特点，预测库岸可靠性的变化趋势更具实际意义。另一方面，由于水文地质条件的不确定性及时变特点，库岸岩土体抗剪强度参数及抗滑力（矩）、下滑力（矩）等作为一个随机过程而存在，以时不变理论来分析评价时变系统的稳定性及安全程度存在明显不足。冯永、罗文强等[9－11]利用随机方法建立了安全系数与可靠性相结合的滑坡稳定性二元评价体系，此方法从静态角度对边坡稳定性进行了分析，未考虑边坡系统中岩土力学性能参数的时变特点。陈昌富等[12]基于极限平衡法，通过算例对比分析了考虑力学强度参数时间和空间效应的边坡最危险滑动面位置及最小安全系数的变化特点，但未对边坡可靠性作进一步研究。李典庆等[13]以香港地区近20年的16000个切坡的观测资料为基础，从降雨角度对边坡进行统计分析，采用概率统计方法确定了随时间的滑坡概率，并提出了边坡的时变可靠性分析方法。但此方法没有考虑边坡稳定控制因素的力学性质随时间变化特点。

当前研究中，考虑库岸在水位反复升降影响下的岩性劣化，对基于水-岩相互作用下的库岸边坡进行可靠性研究相对较少。本文结合当前该领域研究成果，依托富宁港一期工程，以室内岩石力学试验为基础，综合极限平衡法和可靠性理论，提出一种软岩库岸时变稳定性分析及评价方法。

2 工程概况

根据富宁港区岩土体工程地质特征，通过现场勘测，港区地层为中生界三迭统和新生界第四系全新统，其中岩层主要为三叠系中统百蓬组第3段及第 4段地层。结合文献[14]将港区岩体划分为层状结构较硬岩夹软质岩岩组、层状结构软质岩岩组和碎裂结构岩组等3个亚类。港区天然岸坡多为层状结构软质岩岩组和碎裂结构岩组，无规模较大的构造形迹，但发育较多结构面。以库区某一边坡为例，该边坡原始自然坡度约为45°，坡高约为30 m，其地质剖面如图1所示。斜坡主要地层为风化泥岩，节理发育多达6组，密度为10～30条/m，部分组成“X”型共轭节理。评估区内部分岩体呈碎屑状或碎块状，岩体强度较低，遇水易软化，多为软质岩体，属碎裂结构岩组。水库蓄水后，该库岸高低水位差达25 m，在库水位周期性涨落影响下，易形成规模较大的库岸岩体失稳。

图1 库岸地质坡面图Fig.1 The geological profile of reservoir bank

3 库岸时变稳定性分析实现过程

通过室内常规三轴压缩试验，分析岩石试样在干湿循环条件下抗剪强度参数的劣化特点，通过工程方法对其进行转换，经回归分析构建岩体综合抗剪强度参数概率分布的时变模型。考虑库岸的时变特点，其黏聚力和内摩擦角应以随机过程进行描述。实际工程中可以将岩体的抗剪强度参数看作在不同时刻服从不同概率分布的一种随机变量，对于在某一时刻的分析则与一般的概率论和统计学方法相同，即可得到简单的可靠度指标[15－16]。在时刻τ∈[0,T]（其中T表示主体工程的设计基准期），库岸安全系数Fs()τ为一随机变量，依据可靠度理论，求得库岸在时刻 τ∈[0,T]的可靠指标β (τ)和可靠度Pr(τ)。工程中取岩土体各参数的均值计算得到中值安全系数Fso(τ)，并以Fso(τ)近似表示安全系数的数学期望 E[ Fs(τ) ][9－11]。在任意时刻t∈[0,T ]内，以Fso(t)和Pr(t)为库岸的二元评价指标，将库岸的Fso(t)和Pr(t)相乘，得到时变可靠安全系数[9－11]，记为Fsr(t)。最终以库岸的Fsr(t)为标准，定量分析评价库岸的时变稳定性。

4 岩石试样的力学试验

4.1 常规三轴压缩试验

结合港区岩组分布特点，选取具有代表性的中风化泥岩，主要矿物成分为长石、云母，岩层平均厚度为 7.42 m。依据文献[17]，试样按φ50 mm×100 mm标准制作。将试样分7大组，分别模拟泥岩“饱水-风干”0、1、2、3、4、10、15次后的力学特性，每大组再分3小组，每小组5件试样。岩石饱水试验按照文献[17]采用自由浸水法 ，即将试样置于水槽并注水至试样高度的 1/4，以后分 3次注水直至浸没试样，每次注水时间间隔2 h。待试样在水中自由浸水48 h后取出，此时，可认为试样完全饱和。将饱和试样置于烘箱内，在105 ℃恒温下烘干，取出试样待冷却至室温后称重，重复烘干试验步骤，直至试样至恒重（两次称量之差不超过后一次称量的0.1%）。

三轴试验系统采用武汉岩土力学研究所研制的RMT-150C电液伺服试验机。试验中每小组5件试样预定围压分别设定为5、10、15、20、25 MPa。试验开始时对试样加围压至预定值，在不同的预定围压下，通过压缩仪对岩石试样进行等围压压缩。压缩方法采用位移控制，以0.005 mm/s的恒定速率对试样进行加载直至破坏，测得不同干湿循环次数下各试样破坏时的轴向压力，从而得到每小组试样在不同围压下的大、小主应力1σ及σ3。试验过程在计算机的控制下自动进行，试验完成后能自动卸载并退回到初始状态，根据需要提取对应试验结果。每一小组内，综合5组数据通过做摩尔圆包线计算出泥岩试样的黏聚力cR和内摩擦角φR。按照同样方法对不同干湿循环次数下其他各小组岩石试样进行常规三轴压缩得到相应的黏聚力和内摩擦角，从而计算泥岩在“饱和-风干”一定次数后的黏聚力均值和内摩擦角均值，同时计算黏聚力变异系数Var cR和内摩擦角变异系数 Va rφR。各工况下的试验数据如表1所示。

表1 岩石试样常规三轴压缩试验分析数据Table1 The analysis data with conventional triaxial compression test of rock samples

4.2 岩石强度向岩体综合强度的转换

由于实际岩体中存在的节理裂隙等缺陷，通过室内试验所获得的强度参数并不能直接代替实际工程中岩体的综合强度参数。在工程设计中，岩体的抗剪强度参数需依据试验结果进行综合分析和经验判断来确定[18]。目前通常利用费辛柯法、CSIR法、Georgi法、Hoek法、经验折减法等对岩石强度进行转换，从而得到岩体的综合强度[19]。

CSIR法及Georgi法在弱风化的坚硬岩体中比较适用[19]。Hoek法需要较多的地质系统统计参数。经验折减法则需以丰富的工程经验和实地勘察资料为基础。费辛柯法考虑岩体结构面间距和岩体破坏高度两个因素，适用于较软岩层，对岩石试样黏聚力cR进行转换得到岩体的黏聚力c，如下式所示[19－20]：

式中：cR为岩石试样的黏聚力（MPa）；c为转换后岩体的黏聚力（MPa）；a为取决于岩石强度和岩体结构面分布的特征系数；L为破坏岩体被切割的原岩尺寸，取结构面间距（m）；H为岩体破坏高度，取库岸边坡高度（m）。

岩体内摩擦角φ可依据文献[21]由岩石试样内摩擦角cR按岩体裂隙发育程度乘以相应的折减系数来确定。对于裂隙发育的库岸边坡，折减系数可取 0.80～0.85。结合文献[19－21]，计算中取a=10、L=0.03 m、H=30 m；岩石试样内摩擦角φR的折减系数取 0.8[21]。转换后的岩体抗剪强度参数如表2所示。

表2 转换后的岩体抗剪强度参数Table2 The converted shear strength parameters of rock mass

5 泥岩库岸时变稳定性分析

5.1 岩体抗剪强度参数的时变模型

广西百色水利枢纽正常蓄水后，每年 1－5月水位从228 m降至203 m（吴淞高程），6月开始蓄水，7－9月保持在214 m，10月继续蓄水，12月达到228 m。根据实际情况，可假设库岸岩体承受每年一次“饱和-风干”的交替作用。

文献[6－7，12，15]针对岩石（体）力学参数，提出不同的回归模型。本文结合现场勘测及实际工程特点，根据实测数据散点图分布特征，拟采用以负指数形式回归方程对试验数据进行拟合。通过回归分析，得到基于水-岩相互作用下对应参数均值的时变规律，如下式所示：

式（2）、（3）回归相关系数分别为0.986和0.977，t为时间（a），133.766和26.240分别为岩体黏聚力和内摩擦角均值的初始值，其他参数为回归系数。从回归方程可以看出，随着时间的增长（t→∞），黏聚力将变为 0，而内摩擦角则趋近于某一定值。这一变化特点说明天然岩体随时间而风化分解最终变成泥土或完全不具黏聚力的淤泥，而此时内摩擦角即为风化分解后泥土的休止角，这一过程符合地质基本常识[6]。

对于岩体综合抗剪强度参数的变异性，根据试样试验结果，用岩石试样抗剪强度参数的变异性近似代替，经回归分析得到如下模型。

式（4）、（5）回归相关系数分别为0.901和0.904：t为时间（a），0.55和0.40分别为本实例中岩体黏聚力和内摩擦角的最大变异系数[22]，其他参数通过回归分析确定。

5.2 库岸时变中值安全系数

对于裂隙发育的软岩库岸，其滑动面近似为一圆弧[23]。依据极限平衡理论，可通过简化 Bishop法对库岸进行时变稳定性分析。

简化Bishop法考虑条间推力，忽略条间剪力，并假定各条块底部滑动面上的抗滑安全系数均相同，即等于滑动面的平均安全系数。其受力如图 2所示。在任意时刻t，不考虑地震影响时，简化Bishop法的安全系数表达式为

式中：Fs(t)为滑动面的时变安全系数；为考虑时变性后第j条块的有效黏聚力（kPa）；为考虑时变性后第 j条块的有效内摩擦角（°）；bj为第j条块的底面宽度（m）；aj为第j条块的底面倾角（°）；Wj为第 j条块的重力（kN）；uj为第 j条块的孔隙水压力（kPa）。

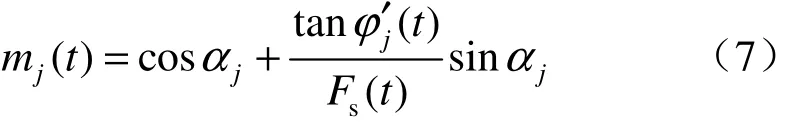
式中：mj(t)同时含有安全系数Fs(t)，故需进行迭代计算求得满足精度要求的安全系数Fs(t)。

图2 简化Bishop法受力分析Fig.2 Force analysis of simplified Bishop method

选取库岸低水位时期为计算工况，考虑地下水位及库水位影响，未考虑降雨、地震以及其他人为因素，根据式（2）、（3），取不同年限内泥岩库岸黏聚力和内摩擦角的均值代入式（6）、（7），计算得到时变中值安全系数Fso(t)，其变化规律如图3所示。

图3 不同年限内库岸中值安全系数Fig.3 The mean safety factor in different years

图3中，岩体抗剪强度参数的时变性导致库岸中值安全系数也具有时变特点，表征着库岸稳定性的逐年降低。水库开始运行后 1～10 a，Fso(t)从1.898下降至1.186，下降幅度为37.51%。水库运行10～50 a，库岸的Fso(t)从1.186下降至1.082，下降幅度为8.77%。可见，水库开始蓄水后，库岸Fso(t)显著下降，随着蓄水次数增加，Fso(t)仍有所降低，但变化趋于稳定。

5.3 库岸时变可靠性

考虑参数的时变性，在已有安全系数的基础上，定义库岸的功能函数，可表示为

在某一时刻τ ∈[0,T]，c(τ)和φ (τ)具有一定的概率分布，大多服从正态分布或对数正态分布[18]。本文结合试验数据，假设c(τ)和φ (τ)服从正态分布，通过蒙特卡洛随机抽样进行可靠性分析。

蒙特卡洛随机抽样是利用计算机产生N个符合要求的随机强度参数c(τ)和φ (τ)并代入式（6）、（7）中，得出随机的安全系数Fs(τ)。经过N次抽样后，其均值和方差分别为 μFs(τ)和。此时库岸的可靠指标为

可靠度为

基于蒙特卡洛随机抽样基本思想，结合式（2）～（5）对不同时刻的库岸黏聚力和内摩擦角进行随机模拟 1000次，得到库岸在不同时刻的β(t)和Pr(t)，其变化规律如图4所示。

图4 库岸时变可靠性曲线Fig.4 The time-varying reliability curves of reservoir bank

库岸抗剪强度参数概率分布的时变性导致安全系数的概率分布也具有时变特点。水库运行 1～10 a，库岸的β(t)从7.563降至1.897，下降幅度为74.92%。Pr(t)从99.99%下降至97.11%，下降幅度为2.88%。水库运行10～50 a，库岸的β(t)由1.897下降至0.381，Pr(t)由97.11%下降至64.83%，下降幅度分别为 79.92%和 33.24%。经分析，随着库水位的周期性涨落，库岸的可靠指标和可靠度表现出显著的非线性时变特点。可靠性的大幅下降也表明库岸安全程度的显著降低。

5.4 库岸时变稳定性分析

单一的安全系数并不能完全表征边坡的安全性。在工程实践中，个别边坡工程安全系数大于设计规范值，认为是安全的情况下，工程失稳破坏仍有所闻[24－25]。主要原因在于常规意义的安全系数不能有效地考虑到边坡稳定控制因素的变异性，也无法评估边坡的可靠性和安全程度。综合考虑库岸抗剪强度参数的时变特点和变异性，以时变中值安全系数和时变可靠度一并作为评价指标，采用时变可靠安全系数为标准能更合理地分析库岸的时变稳定性。

对于本文算例，其时变中值安全系数Fso(t)，时变安全系数均值μFs(t)（时变安全系数的数学期望E[ Fs(t)]）以及时变可靠安全系数Fsr(t)的变化过程如图5、6所示，库岸最危险滑动面变化过程如图7所示。

图5 库岸安全系数变化图Fig.5 The change chart of reservoir bank safety factors

图6 库岸安全系数对比图Fig.6 The comparison chart of reservoir bank safety factors

图7 不同年限内最危险滑动面变化图Fig.7 The trend chart of the most dangerous slip surfaces in different years

由图5～7可知：

（1）通过蒙特卡洛随机抽样求得的安全系数均值仅考虑随机安全系数的平均水平，没能考虑离散程度，所得结果能较好地与中值安全系数重合（最大差值为0.029，t=50 a）。在库岸时变稳定性分析中，时变中值安全系数及时变安全系数均值表征库岸的稳定性有所降低，但不能真实地反映库岸稳定性的变化情况。二者只能作为参考指标而不能作为最终的评价标准。

（2）由于岩体抗剪强度参数前期变异性较小，库岸时变中值安全系数、时变安全系数均值与时变可靠安全系数在水库运行后1～10 a内吻合较好。随着抗剪强度参数变异性的增大，库岸可靠度随时间显著降低，由此导致时变中值安全系数与时变可靠安全系数呈现出不同的衰变规律。

（3）不考虑库岸的时变性，中值安全系数（t=0 a，Fso=1.898）和可靠度（t=0a，Pr=99.99%)为一定值。实际上，库岸的稳定性和安全程度会逐年降低，表现为一种劣化模式，其最危险滑动面变化趋势也由内侧向外侧扩展，表现为一种渐进性破坏。

（4）考虑时间因素的单一指标（时变中值安全系数或时变安全系数均值）或不考虑时间因素的二元指标（结合安全系数和可靠度的可靠安全系数）仅适宜对库岸进行短期的稳定性分析，并不能作为库岸时变稳定性的评价指标。以可靠安全系数Fsr＞1为标准评价库岸的稳定性，则t=15 a时，可靠安全系数 Fsr=1.061，库岸将处于临界状态，应根据实际工程情况及时进行加固治理。

6 结 论

（1）针对库岸边坡存在的时变性，构建出泥岩抗剪强度参数概率分布的时变模型，得到泥岩在水位周期性涨落下，抗剪强度参数存在的非线性时变特点：水库运行1～10 a内，均值衰变明显，第10年后衰变趋于稳定；变异性呈现出非线性的增大趋势，最终趋近于某一确定值。

（2）采用提出的泥岩库岸时变稳定性分析方法，得到库岸时变中值安全系数Fso(t)、时变可靠度Pr(t)以及时变可靠安全系数Fsr(t)的变化特征，同时获知该库岸最危险滑动面位置的变化特点。分析表明：泥岩抗剪强度参数概率分布的时变性对库岸长期稳定和安全程度有显著影响，忽略时变效应和变异特性所得结论具有一定的局限性。

（3）在实际工程中，采用本文提出的库岸时变稳定性分析方法能为库岸的风险分析，加固时间等提供理论依据和参考价值。

（4）本文从试验数据出发，得到基于水-岩相互作用下泥岩力学参数的变化特性，将随机过程离散成某一时刻的随机变量，从统计学角度建立抗剪强度参数概率分布的时变模型，避免了利用随机过程作为时间序列而建立纯理论模型的数学困难。在实际工程中，可结合本文的基本思想和应用方法进行综合考虑，从而构建更为复杂的库岸时变稳定性分析模型。

（5）本文结果根据室内试验的7组试验数据经相关计算得到，实际工程中岩体力学性能劣化受多方面因素影响，对于不同的地质水文条件下岩体力学参数的劣化规律有待进一步深入研究。

[1]FUJITA T,NGUYEN T,HERNELIND J,et al. Hydromechanical response of a fractured granitic rock mass to excavation of a test pit—the Kamaishi Mine experiment in Japan[J]. International Journal of Rock Mechanics and Mining Sciences,2001,38(1): 79－94.

[2]王均星,李泽,陈炜. 考虑孔隙水压力的土坡稳定性的有限元下限分析[J]. 岩土力学,2005,26(8): 1258－1262.WANG Jun-xing,LI Ze,CHEN Wei. Lower bound analysis of soil slope stability using finite elements subjected to pore water pressure[J]. Rock and Soil Mechanics,2005,26(8): 1258－1262.

[3]刘才华,陈从新,冯夏庭,等. 地下水对库岸边坡稳定性的影响[J]. 岩土力学,2005,26(3): 419－422.LIU Cai-hua,CHEN Cong-xin,FENG Xia-ting,et al.Effect of groundwater on stability of slopes at reservoir bank[J]. Rock and Soil Mechanics,2005,26(3): 419－422.

[4]王明华,晏鄂川. 水库蓄水对岸坡滑坡的影响研究[J].岩土力学,2007,28(12): 2722－2725.WANG Ming-hua,YAN E-chuan. Study of influence of reservoir water impounding on reservoir landslide[J].Rock and Soil Mechanics,2007,28(12): 2722－2725.

[5]张明,胡瑞林,崔芳鹏. 考虑水-岩物理化学作用的库岸堆积体边坡稳定性研究——以金沙江下咱日堆积体为例[J]. 岩石力学与工程学报,2008,27(增刊2): 3699－3704.ZHANG Ming,HU Rui-lin,CUI Fang-peng. Stability study of reservoir accumulation body considering physical and chemical reactions between water and accumulation body—taking Xiazanri accumulation body for example[J]. Chinese Journal of Rock Mechanics and Engineering,2008,27(Supp. 2): 3699－3704.

[6]刘新荣,傅晏,王永新,等.（库）水-岩作用下砂岩抗剪强度劣化规律的试验研究[J]. 岩土工程学报,2009,30(9): 1298－1302.LIU Xin-rong,FU Yan,WANG Yong-xin,et al.Deterioration rulers of shear strength of sand rock under water-rock interaction of reservoir[J]. Chinese Journal of Geotechnical Engineering,2009,30(9): 1298－1302.

[7]傅晏,刘新荣,张永兴,等. 水-岩相互作用对砂岩单轴强度的影响研究[J]. 水文地质工程地质,2009,(6):54－58.FU Yan,LIU Xin-rong,WANG Yong-xing,et al. Study of the influence of water-rock interaction to the strength of sandstone[J]. Hydrogeology and Engineering Geology,2009,(6): 54－58.

[8]刘新荣,傅晏,王永新,等. 水—岩相互对库岸边坡稳定的影响研究[J]. 岩土力学,2009,30(3): 613－616.LIU Xin-rong,FU Yan,WANG Yong-xin,et al. Stability of reservoir bank slope under water-rock interaction[J].Rock and Soil Mechanics,2009,30(3): 613－616.

[9]冯永,赵文斌,罗文强. 基于随机分析的滑坡稳定性二元评价方法[J]. 煤田地质与勘探,2006,34(5): 42－44.FENG Yong,ZHAO Wen-bin,LUO Wen-qiang. Dual evaluation method of landslide stability based on stochastic analysis[J]. Coal Geology & Exploration,2006,34(5): 42－44.

[10]罗文强,王亮清,龚珏. 正态分布下边坡稳定性二元指标体系研究[J]. 岩石力学与工程学报,2005,24(13):2288－2292.LUO Wen-qiang,WANG Liang-qing,GONG Jue. Study of slope stability by dual index system based on normal distribution[J]. Chinese Journal of Rock Mechanics and Engineering,2005,24(13): 2288－2292.

[11]罗文强,龚珏,王洪兴. 边坡稳定性二元指标体系与应用研究[J]. 地球科学进展,2004,19(增刊): 300－304.LUO Wen-qiang,GONG Jue,WANG Hong-xing. Study of slope stability by dual index system and its application[J]. Advance in Earth Sciences,2004,19(Supp.): 300－304.

[12]陈昌富,秦海军. 考虑强度参数时间和深度效应边坡稳定性分析[J]. 湖南大学学报(自然科学版),2009,36(10): 1－6.CHEN Chang-fu,QIN Hai-jun. Stability analysis ofslopes considering the time and depth effect of strength parameters[J]. Journal of Hunan University (Natural Sciences),2009,36(10): 1－6.

[13]李典庆,吴帅兵. 考虑时间效应的滑坡风险评估和管理[J]. 岩土力学,2006,27(12): 2239－2249.LI Dian-qing,WU Shuai-bing. Landslide risk assessment and management considering time effect[J]. Rock and Soil Mechanics,2006,27(12): 2239－2249.

[14]中华人民共和国建设部. GB 50021－2001岩土工程勘察规范[S]. 北京: 中国建筑工业出版社,2001.

[15]许宏发,陈力新. 岩石时效特性与节理模型[M]. 上海:上海交通大学出版社,2009.

[16]FRANGOPOL D M,LIN K Y,ESTES A C. Reliability of reinforced concrete girders under corrosion attack[J].Journal of Structural Engineering,1997,123(3): 286－297.

[17]中华人民共和国建设部. GB/T 50266－1999工程岩体试验方法标准[S]. 北京: 中国标准出版社,1999.

[18]陈祖煜,汪小刚,杨健,等. 岩质边坡稳定性分析[M].北京: 中国水利水电出版社,2005.

[19]杨永兵. 边坡岩石强度与岩体强度的工程变换[J]. 金属矿山,2004,(9): 10－12.YANG Yong-bing. Engineering conversion of strength between slope rock and rock mass[J]. Metal Mine,2004,(9): 10－12.

[20]陈志坚,孙英学. 裂隙岩体力学参数的弱化处理[J]. 江苏地质,2000,24(1): 36－38.CHEN Zhi-jian,SUN Ying-xue. Weakening treatment to the mechanic parameters of fissured rock mass[J].Jiangsu Geology,2000,24(1): 36－38.

[21]重庆市建设委员会. GB 50330－2002建筑边坡工程技术规范[S]. 北京: 中国建筑工业出版社,2002.

[22]四川省交通厅交通勘察设计研究院. 云南富宁港建设一期工程地质勘察报告[R]. 四川: 四川省交通厅交通勘察设计研究院,2008.

[23]刘特洪,林天健. 软岩工程设计理论与施工实践[M].北京: 中国建筑工业出版社,2001.

[24]姚爱军,薛延河. 复杂边坡稳定性评价方法与工程实践[M]. 北京: 科学出版社,2008.

[25]罗文强,张倬元,黄润秋. 边坡系统稳定性的可靠性研究[J]. 地质科技情报,1999,18(2): 62－64.LUO Wen-qiang,ZHANG Zhuo-yuan,HUANG Run-qiu.Research on stability of slope system in reliability theory[J]. Geological Science and Technology Information,1999,18(2): 62－64.