一维小变形主、次固结耦合理论模型分析
仇玉良,丁洲祥,
(1.北京交通大学 土木建筑工程学院,北京 100044;2.中国矿业大学 深部岩土力学与地下工程国家重点实验室,江苏 徐州 221008)
1 引 言
土体的变形与时间有关,既包含超静孔压消散逐渐转换为有效应力带来的影响,也包含有效应力与应变关系的不惟一而与时间有关所产生的影响,前者称为主固结效应,后者称为次固结效应[1]。土体的主、次固结效应一直是土力学研究中的一个重要问题。经典 Terzaghi固结理论假定土体的应力-应变关系是线性、弹性和与时间无关的,这与土体实际上的应力-应变时间相关性相矛盾。
为了克服Terzaghi理论的这一局限性,历史上曾提出了不少改进方法。Ladd等[2]将这些改进的固结理论概括为假说A和假说B,如图1所示。

图1 Ladd等[2]提出的假说A和BFig.1 Hypotheses A and B proposed by Ladd et al.[2]
假说A将主固结变形和次固结变形截然分开,用Terzaghi理论计算主固结变形,而用次固结系数计算主固结完成后的蠕变变形。假说A隐含着一个假定,即在主固结完成时,土体应力-应变关系是惟一的,并且与土层厚度无关,但该假定与大量试验结果相左[3]。假说B假定蠕变出现在整个固结过程中,这与连续介质力学中的流变学和黏塑性理论一致[3],机制较为严谨,近年来不少学者倾向于支持此观点[4]。在假说B范畴内,殷建华等[3,5]提出了著名的EVP模型,并基于该模型的固结分析模拟了孔隙水压力升高和有效应力减小的现象,这一现象已经在若干现场试验中得到证实,但之前从未被其他模型和固结理论所解释。丁洲祥等[6]提出了一个考虑大变形的主、次固结耦合新模型,将主、次固结效应问题的研究推广到考虑大变形,即材料非线性和几何非线性的情况。
本文将根据丁洲祥等[6]新近提出的模型的一个退化模型,探讨在一维小变形情况下,主、次固结耦合发展的一般规律,通过分析也发现了EVP模型所预测到的孔压升高和有效应力减小的现象。此外,还就主、次固结耦合机制和模型中新参数的合理确定等问题进行探讨,为主、次固结耦合理论及工程应用研究提供新的参考。
2 一个小变形主、次固结耦合模型
首先引入以下3个假设条件:
(1)不考虑土体重度变化、固相速度、地表沉降速度、地下水位变化(土体始终位于地下水位以下)以及荷载变化等因素的影响;
(2)土体变形很微小;
(3)渗透系数为常数。
丁洲祥等[6]提出的基于超静孔压为控制变量的一维大变形主、次固结耦合模型就可以退化为小变形主、次固结耦合模型

式中:u为超静孔压;t为时间;e0为初始孔隙比;γw为孔隙水的重度;k为渗透系数;av为压缩系数;z为普通的纵坐标;Cα为次固结系数。
可以将式(1)简记为

式中:Cv为经典Terzaghi固结理论中的固结系数;Cps为新引入的主、次固结耦合系数,两者分别定义为

当Cps=0,即Cα=0不考虑次固结影响时,式(2)就退化为经典的Terzaghi固结理论模型。或者说,式(2)是Terzaghi理论向考虑主、次固结耦合方向发展的一个模型。
式(2)对应的无量纲形式为

式中:u0为外荷载引起的初始超静孔压;H为排水路径的长度;Csc为无量纲的主、次固结耦合系数。
正常固结均质土体在单面排水(上边界排水、下边界不透水)和瞬时加荷情况下的初、边值条件分别为

模型式(5)及式(10)~(12)构成一个定解问题,可以采用有限差分解法进行数值分析。考虑到有限差分技术已经发展成为较成熟的分析方法,这里对该方法不再详述,可参考文献[7]。由于Crank-Nicolson格式具有二阶精度和无条件稳定性,本文采用该格式进行计算。
3 数值分析
3.1 超静孔压随时间的发展规律
算例分析拟针对正常固结均质土体在单面排水和瞬时加荷情况下超静孔压的发展规律进行对比和讨论,有关数据均采用无量纲量。
图2给出了底部不透水边界(Z=1)上的超静孔压U随时间因数T的发展规律。在固结起始时刻,超静孔压不是像经典Terzaghi模型预测的那样不断减小,而是表现出不断增加,直至达到某一极大值后才呈现不断消散而下降的趋势。主、次固结耦合无量纲系数Csc对超静孔压发展规律具有较大影响。当Csc=0时,超静孔压曲线上观察不到孔压值升高的特殊现象,这是因为此时的主、次固结耦合模型完全退化为Terzaghi模型的缘故。而随着Csc在数值上依次从0.05、0.10、0.20增大到0.40,固结初期的超静孔压增大的现象越来越突出。这一现象是经典 Terzaghi理论所不能解释的。而著名的Mandel效应也无法解释。Mandel效应解释了总应力增加情况下超静孔压的异常增大,相应的有效应力未必降低;而此处为总应力不变情况下超静孔压超过外荷载的特殊情况。由于这里的问题属于一维情况,因此,总应力保持不变,超静孔压的增大必然会引起有效应力的降低,这是显著区别于Mandel效应之处。

图2 不透水边界上的超静孔压U随时间因数T的发展Fig.2 Development of excess pore pressure U with time factor T at impervious boundary
殷建华等[5,8]利用EVP模型先后对理想黏土层的一维和多维固结进行模拟分析,较早发现在常荷载条件下,孔隙水压力的升高及相应的有效应力减小的现象,并认为其机制是黏性(蠕变)效应。本文模型也同样可预测到此效应,并且在模型上更为简洁。
3.2 超静孔压的时空分布规律
超静孔压U沿埋深Z的空间分布规律如图3所示。其中,时间因数T分别取T=0.090241和T=0.611807作为典型时刻,无量纲主、次固结耦合系数Csc分别取0.00、0.05、0.10、0.20和0.40进行对比。
在地表Z=0处,超静孔压始U终为0,符合排水边界条件假设。随着埋深的增加,不同主、次固结耦合系数Csc对应的超静孔压之间的差别越来越大,在不排水边界,即Z=1处相应的偏差达到最大值。在同一埋深Z处,随着Csc的增大,考虑主、次固结耦合的超静孔压U值愈加偏大于仅考虑主固结即Csc=0的情况,反映了次固结效应的影响。

图3 超静孔压U沿埋深Z的分布规律Fig.3 Variations of excess pore pressure U with depth Z
图4分别给出了不同Csc值对应的超静孔压随埋深和时间发展的三维曲面。其中,图4(a)中的Csc取为0,反映了不考虑次固结情况下Terzaghi主固结理论预测的超静孔压的时空变化规律。从中清楚可见,不同埋深处的超静孔压随时间因数增加而趋于消散的整个过程,并且在固结初期并没有出现超静孔压增大的现象,这是符合理论解释的。
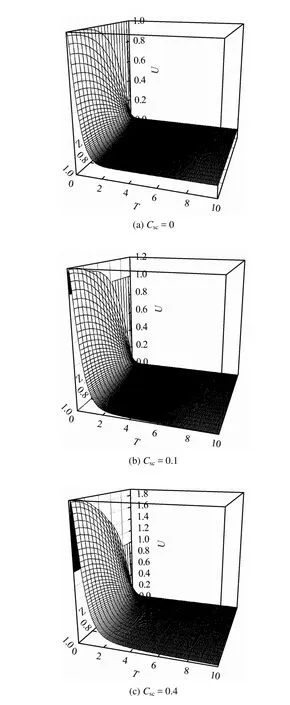
图4 超静孔压的时空分布规律Fig.4 Distributions of excess pore pressure along time and spatial domain
图4(b)、4(c)分别给出了Csc取代表值0.1和0.4时超静孔压的时空分布规律。在固结初期,不排水边界附近土体的超静孔压出现先增大而后才逐渐消散的现象,而在近排水边界附近,土体超静孔压随时间发展不断消散,没有出现超静孔压增大的现象,这是由于在排水边界附近,土体超静孔压易于消散的缘故。主、次固结耦合系数Csc取较大值时,在土体主、次固结耦合发展过程中次固结效应表现更加突出,固结初期的超静孔压会有更大的增加。可见,考虑主、次固结耦合的情况下,土体中的超静孔压发展规律明显不同于经典Terzaghi固结理论的结果,这也可作为从超静孔压发展角度,区别主、次固结机制的判断条件之一。国内外均有不少关于土体超静孔压增加,而Biot理论和Mandel效应均无法解释的工程实例报道[3,5]。鉴于主、次固结机制存在本质不同,以往通过调整主固结系数来拟合工程实测的超静孔压或沉降速率的传统方法,可能会存在一定局限性,尤其在初期孔压升高的情况下。因此,在固结机制研究中考虑次固结效应,可为解释此类现象提供理论分析依据,具有较好的工程应用前景。
4 讨 论
4.1 关于主、次固结耦合机制
4.1.1 早期认识
Taylor和 Merchant[9]在 MIT首次尝试对Terzaghi固结理论进行完善,认为固结过程中的孔隙比是时间t和有效应力σ′的函数,e=f(σ′,t)。因此,孔隙比的变化率为

对式(13)进行积分,

作为选择,式(14)也可表述为

式中:tp为主固结结束或次固结开始的时刻。
对比式(14)与式(15),当t>tp时,dσ′/d t=0。式(15)右端第1积分项表示主固结阶段,而第2积分项则表示次固结阶段。显然,(∂e/∂σ′)t和(∂e/∂t)σ′两者均对主固结压缩有贡献,而且只要(∂e/∂t)σ′不为0,次固结变形就不会停止发展[10]。
4.1.2 两类假说的争议
龚晓南[4]认为,产生次固结的机制研究尚未取得一致意见,大致可以分为以陈宗基为代表的“次固结就是蠕变”和De Jong为代表的“次固结是更为细小的孔隙网络中的水力固结”等两大类观点[4]。曾玲玲等[11]还从土体结构性角度深入研究了软土的次固结机制,但尚未讨论有关的主、次固结耦合问题。相对而言,国际上较普遍接受的是Ladd等[2]总结提出的假说A和假说B分别对应于不同的主、次固结耦合机制。
国内若干著作中关于次固结机制的解释大多可归于假说A。例如,钱家欢[12]认为,次固结发生在固结后期,此时超静孔压虽已消散为 0,但土粒表面的吸着水层受压变形,离开土粒表面较远的那部分吸着水逐渐转变为自由水,这样引起的地基土的压缩产生次固结沉降,并持续时间极长。李广信[13]、黄文熙[14]对沉降类型的划分中,提到次压缩沉降基本上发生在土中超静孔压完全消散以后,是在恒定有效应力下的沉降。陈希哲[15]认为,次固结是地基在外荷载作用下经历很长时间,土体中超孔隙水压力已完全消散,在有效应力不变的情况下,由土的固体骨架长时间缓慢蠕变所产生的沉降成为次固结沉降。
近些年来,国际上有不少研究成果开始倾向于支持假说B而否定假说A。其中,日本学者在此方面也作了一定贡献,例如 Murakami[16]对主固结阶段即超静孔压消散过程中的次压缩(次固结)特性进行了试验研究,认为主固结阶段的次压缩应变随着黏土层厚度的增加而增大,仅当有效应力超过准先期固结压力时次压缩才会发生并可表述为压缩历时和压缩应变的某一函数;Imai等[17-18]采用内联固结仪,通过试验验证了主固结过程中存在蠕变压缩,还提出了相应的数学模型。值得注意的是,也出现了一种反对意见,Mesri[10]认为过去研究中拒绝假说A或支持假说B的原因在于使用了一些误导性的解释。Ladd等[2]的假说B采用流变模型进行预测,其中蠕变作为单独的现象产生作用,Mesri[10]认为,蠕变在主固结阶段也发生作用,并不是一个独立现象,因为(∂e/σ′)t和(∂e/∂t)σ′相互作用并且均依赖于dσ′/dt和tp。因此,假说B未必正确。另一方面,Jamiolkowski等[19]在重述假说A和B的定义时,认为假说A假定蠕变仅在主固结结束后才发生,这与国内若干著作和常用教材所述基本一致。根据Jamiolkowski等[19]的这一假定,同时注意到蠕变的确在主固结阶段就已发生,于是Leroueil断定假说A 是错误的[10]。此外,Mesri[10]还纠正了以往认识的主固结阶段没有次固结发生的错误,因为式(15)右端第1项中含有(∂e/∂σ′)t项;他甚至认为,目前还未有可靠的室内试验或现场测试数据证明假说B的合理性。
可见,关于主、次固结耦合机制的认识目前仍处于探索抑或争议阶段。在此背景下,本文模型的特点是属于全时程的主、次固结耦合模型,即直接运用式(14)而非式(15),这样就避免了应用中难以确定tp的问题。在新模型中土体超静孔压分别由主、次固结机制引起,并耦合在一起同时发展,这样对于固结后期,仍然存在超静孔压的消散,而不是某些文献所谓的超静孔压为0。
4.1.3 超静孔压的发展
关于次固结阶段的超静孔压问题,笔者认为,在两相不可压缩的前提下,如果饱和土的次固结仅仅引起压缩变形而不产生超静孔压,则从连续介质力学的基本原理来看,将违背质量守恒定律。因为按质量守恒定律,次固结引起土体体变的过程必定伴随着孔隙水的排出,而孔隙水的流动理应源于超静孔压的不均匀分布和发展,超静孔压不应为 0,否则就不会有体变发生。从这种意义上看,De Jong为代表的次固结[4]是一种特殊意义的水力固结的观点具有一定的合理性。Mitchell和Soga[20]的新近观点也修正了以往认为的次固结阶段没有超静孔压的片面认识,即在次固结(次压缩)阶段,土体内部和边界之间应存在某一小的静水压力差。这些认识和本文模型思想基本一致。

图5 主、次固结分别引起的超静孔压随时间的发展规律(不排水边界上)Fig.5 Variations of excess pore water pressure with time caused respectively by primary and secondary consolidations (at impervious boundary)
根据本文模型,图5给出了主、次固结耦合系数Csc分别取值0.1和0.2时,主、次固结机制各自引起的不排水边界上超静孔压U随时间因数T的发展规律。其中,主固结机制引起的超静孔压按Terzaghi理论即Csc取0计算而得,次固结机制引起的超静孔压按本文模型Csc取0.1和0.2时的结果减去对应的Csc取 0的结果而得。可见,主、次固结机制分别引起的超静孔压随着时间共同发展,在固结初期,次固结引起的超静孔压随时间发展出现增大而非消散的现象,如前文所述;对固结后期,主固结引起的超静孔压相比次固结引起的超静孔压消散得更快,并在量值上小于后者的结果,出现“次固结占优”的现象。从这种意义上看,通常说的主(次)固结阶段改述为主(次)固结占优阶段似乎更合适一些。
进一步分析,如果以国际上的一种观点,即不排水边界上超静孔压消散至 99%作为主固结的结束[10,18]时间tp,那么按图5所示规律,此后的超静孔压不是不产生,而仍在发展,只不过其量值总体上已经非常小。对于Csc=0.05的情况,按本文模型和处理方法,当T=3.16时不排水边界上的超静孔压消散将达到99%。此时,次固结引起的超静孔压值将超出主固结引起的超静孔压值达17.8倍左右。此后,这一高达1个数量级的相对偏差将趋于不断增大,说明次固结阶段的主、次固结耦合将转变为以次固结机制为主。这一结论可为工程上常用的确定次固结系数Cα的方法提供新的理论参考和依据。
4.2 关于新参数Csc
模型参数的合理确定是理论模型面向工程应用的关键问题之一。下面讨论新参数Csc的确定方法。
4.2.1 Cα/Cc概念的应用
Mesri和 Godlewski提出了Cα/Cc概念[21],这一概念目前已获得业界认可和应用[22-23]。Mesri和Castro[24]认为,Cα/Cc连同EOP e-logσ′曲线完整地定义了各类土体的次压缩(次固结)特性。一般地,在固结压力范围内,当Cc随有效应力σ′保持不变、减小或增大时,相应地有Cα随时间保持不变、减小或增加,Mesri通过大量试验数据分析后认为

式中:C为试验常数。对于大量的天然材料,包括泥炭、有机淤泥、高灵敏性黏土、页岩以及颗粒材料,C的数值一般介于0.02~0.10范围内。对于大部分无机软黏土而言,C=0.04 ± 0.01;而对高塑性有机黏土,C=0.05 ± 0.01。
对于本文情况,考虑到式(16)及式(17)

这样,式(4)的Cps就可表示为

这表明在 Cα/Cc为常数概念的基础上,Cps与有效应力σ′成正比例关系。
再将式(18)代入式(9),得到Csc的计算公式

可见,随着固结过程中有效应力σ′的增大,Cps和Csc也将增大,按本文模型来分析,固结后期的次固结效应将愈加显著。结合式(19)与Mesri和Castro[24]研究结果,还可以得到一个较实用的初步结论:大部分无机软黏土的Csc值在固结过程中一般不超过0.03~0.05。
4.2.2 Csc变量的应用
如果进一步考虑到Csc是一个变数,随着固结过程和有效应力σ′的发展而变化,为了应用方便,可将式(5)所示的模型简化为

这样,就可以采用试验常数C代替变数Csc,但相应的代价是,模型的合理性和适用范围将受到Cα/Cc概念的限制。关于模型式(20)的求解,同样可有多种选择,其定量分析结果应该有别于前文,但一般不会改变前文有关的定性认识,因篇幅所限,这里不再做深入讨论。
4.2.3 主、次固结耦合模型的完善方向
在固结过程的不同阶段中,如何合理地考虑和确定有关参数的变化规律在模型应用和发展中居于核心地位。借鉴Imai等[17]内联固结试验结果及其处理方法[16],可以得到主固结过程中有效应力为常数情况下的e-lgt曲线,由此可以较好地确定主固结过程中的次固结系数即式(1)中的Cα,或式(2)中主次固结耦合系数Cps。作为初次讨论,为简便起见,前文的主、次固结耦合分析结果实质上存在主、次固结占优阶段Cα均为同一常数的简化假定,隐含了一定的适用条件。考虑到在主或次固结占优阶段,有效应力保持不变条件下e-lgt曲线的斜率或Cα值可能受到应力水平等因素影响存在或大或小的变化,针对某一给定土体开展相关的试验研究,结合试验结果对主、次固结耦合理论模型进行修正和完善,也是值得加强研究的重要方向。
总的来看,正如任何模型都有其优缺点,本文模型也存在一些其他缺点,主要是数学上时间因数T在零点引起模型奇异性,这源于工程上依据e-lgt关系确定次固结系数Cα的传统方法带来的固有局限性。类似缺点在土力学范畴内并不少见,例如对于e-lgσ′一维压缩本构关系,当有效应力为0时也将导致模型表现出奇异性(即孔隙比为无穷大),但由于该模型的简洁性及其能够反映土体的基本压缩变形特性的原因,e-lgσ′本构关系仍然在工程上得到普遍应用。为避免零点奇异的缺点,本文暂取T的最小值为0.01,而如何在数学的严格性上对本文模型进行完善,还有待结合土体主、次固结耦合机制研究进展进行更深入的研究。换个角度看,按照 Mesri[10]的观点——鉴于主固结过程中(∂e/∂σ′)t和(∂e/et)σ′的一般特性仍是未知的,对应的完善的主固结理论还不存在,主、次固结耦合理论及其工程应用的研究依然任重道远。
5 结 论
(1)本文根据丁洲祥等[6]提出的大变形主、次固结耦合模型的一个小变形退化模型,研究了其无量纲表述的一维主、次固结耦合超静孔压的发展规律。模型中引入了新的主、次固结耦合系数Csc,可作为主、次固结耦合程度的评价指标。Csc为 0时,模型退化为经典Terzaghi主固结模型,而随着Csc的增大,固结过程中的次固结效应愈加突出。
(2)通过对单面排水一维瞬时加载并维持不变算例的有限差分法分析,结果表明,在固结初期,超静孔压出现增大的现象;在整个固结过程中,考虑主、次固结耦合的超静孔压预测值要偏大于不考虑次固结的相应结果,这是次固结机制的反映,与殷建华等[5]研究结果基本一致。不同的是,本文模型仅采用Csc反映主、次固结耦合机制,数学上更为简洁,便于应用。
(3)在两相不可压缩和不违背质量守恒原理的前提下,固结后期同样应存在超静孔压的消散过程,相应的主、次固结耦合机制将表现出次固结机制占优的特点;以不排水边界上超静孔压消散度达99%作为主固结的结束或由此确定次固结系数,从工程精度来看是可行的。
(4)基于Mesri和Godlewski[21]的 Cα/Cc概念,笔者讨论提出了模型中主、次固结耦合系数Csc的确定方法及其取值范围,还据此得到一种改进的主、次固结耦合模型式(20)。鉴于问题的复杂性,主、次固结耦合理论及其工程应用的研究仍亟待进一步完善和加强。
[1]赵维炳,施健勇. 软土固结与流变[M]. 南京: 河海大学出版社,1995.
[2]LADD C C,FOOT R,ISHIHARA K,et al. Stressdeformation and strength characteristics[C]//Proceedings of the 9th International Conference on Soil Mechanics and Foundation Engineering. Tokyo: [s. n.],1977: 421-449.
[3]殷建华,CLARK J I. 土体与时间相关的一维应力-应变性状、弹黏塑性模型和固结分析[J]. 岩土力学,1994,15(3): 65-80.YIN Jian-hua,CLARK J I. One-dimensional time dependent stress-strain behaviour of soils,elastic viscoplastic modelling,and consolidation analysis[J]. Rock and Soil Mechanics,1994,15(3): 65-80.
[4]龚晓南. 高等土力学[M]. 杭州: 浙江大学出版社,1996.
[5]殷建华,CLARK J I. 土体与时间相关的一维应力-应变性状、弹黏塑性模型和固结分析(续)[J]. 岩土力学,1994,15(4): 65-75.YIN Jian-hua,CLARK J I. One-dimensional time dependent stress-strain behaviour of soils,elastic viscoplastic modelling,and consolidation analysis(continued)[J]. Rock and Soil Mechanics,1994,15(4):65-75.
[6]丁洲祥,袁大军,朱合华. 一维大变形主、次固结耦合新模型[J]. 岩土力学,2010,31(8): 2367-2372.DING Zhou-xiang,YUAN Da-jun,ZHU He-hua. A novel coupling model for 1D finite-strain primary-secondary consolidation[J]. Rock and Soil Mechanics,2010,31(8):2367-2372.
[7]张文生. 科学计算中的偏微分方程有限差分法[M]. 北京: 高等教育出版社,2006.
[8]殷建华,朱俊高. 软土弹黏塑性固结模拟[J]. 岩土工程学报,1999,21(3): 360-365.YIN Jian-hua,ZHU Jun-gao. Elastic visco-plastic consolidation modelling of soft clay[J]. Chinese Journal of Geotechnical Engineering,1999,21(3): 360-365.
[9]TAYLOR D W,MERCHANT W. A theory of clay consolidation accounting for secondary compression[J].Journal of Mathematics and Physics,1940,19(3): 167-185.
[10]MESRI G. Primary compression and secondary compression[C]//Soil Behavior and Soft Ground Construction. [S. l.]: ASCE Geotechnical Special Publication,2001: 122-166.
[11]曾玲玲,刘松玉,洪振舜,等. 天然沉积软黏土的次固结变形机制分析[J]. 岩土工程学报,2010,32(7): 1042-1047.ZENG Ling-ling,LIU Song-yu,HONG Zhen-shun,et al.Deformation mechanism of secondary consolidation of natural clays[J]. Chinese Journal of Geotechnical Engineering,2010,32(7): 1042-1047.
[12]钱家欢. 土力学[M]. 南京: 河海大学出版社,1988.
[13]李广信. 高等土力学[M]. 北京: 清华大学出版社,2004.
[14]黄文熙. 土的工程性质[M]. 北京: 水利电力出版社,1983.
[15]陈希哲. 土力学地基基础(第4版)[M]. 北京: 清华大学出版社,2004.
[16]MURAKAMI Y. Secondary compression in the stage of primary consolidation[J]. Soils and Foundations,1988,28(3): 169-174.
[17]IMAI G,TANAKA Y,SAEGUSA H. One-dimensional consolidation modeling based on the isotach law for normally consolidated clays[J]. Soils and Foundations,2003,43(4): 173-188.
[18]IMAI G,TANG Y. A constitutive equation of onedimensional consolidation derived from inter-connectedtests[J]. Soils and Foundations,1992,32(2): 83-96.
[19]JAMIOLKOWSKI M,LADD C C,GERMAINE J T,et al.New developments in filed and laboratory testing of soils[C]//Proceedings of the 11th Conference on Soil Mechanics and Foundation Engineering. San Francisco: A.A. Balkema,1985: 57-153.
[20]MITCHELL J K,SOGA K. Fundamentals of soil behavior (third edition)[M]. Hoboken,New Jersey: John Wiley & Sons Inc.,2005.
[21]MESRI G,GODLEWSKI P M. Time and stresscompressibility interrelationship[J]. Journal of the Geotechnical Engineering Division,ASCE,1977,103(5): 417-430
[22]AL-SHAMRANI M A. Applying the hyperbolic method and Cα/Cc concept for settlement prediction of complex organic-rich soil formations[J]. Engineering Geology,2005,77(1-2): 17-34.
[23]冯志刚,朱俊高. 软土次固结变形特性试验研究[J]. 水利学报,2009,40(5): 583-588.FENG Zhi-gang,ZHU Jun-gao. Experimental study of secondary consolidation behavior of soft soils[J]. Journal of Hydraulic Engineering,2009,40(5): 583-588.
[24]MESRI G,CASTRO A. Cα/Ccconcept and K0 during secondary compression[J]. Journal of Geotechnical Engineering,1987,113(3): 230-247
——结构相互作用的影响分析

