钢板桩挡墙主动土压力分布的形状效应

刘 芳 ，张国庆 ，蒋明镜 ，熊巨华 ，中山裕章

(1. 同济大学 土木工程学院地下建筑与工程系，上海 200092；2. 同济大学 岩土及地下工程教育部重点实验室，上海 200092；3. 新日本制铁株式会社，千叶 日本 293-8511)

1 引 言

钢板桩边缘带有联动装置，可以自由组合形成连续紧密挡土或者挡水墙的钢结构体。近年来随着低碳、绿色、环保等理念深入人心，钢板桩作为一种可重复利用的绿色环保支挡结构，在水利及海岸工程中得到进一步推广。但是，人们对钢板桩土压力分布规律的认识尚不够深入，目前仍采用基于经验的半理论设计方法，钢板桩的理论研究远落后于工程实践，制约着钢板桩的推广和应用。

挡土墙土压力是个古老的问题，在经典土压力计算理论的基础上，大量学者通过室内试验(Fang等[1])、理论分析(王元战等[2]、应宏伟等[3]、张建民等[4])、有限元计算(陈页开等[5－6])及离散元模拟(周健等[7])等手段对此开展了卓有成效的研究。然而，这些研究都基于平面挡墙，对钢板桩土压力方面的研究还很少见。

DiBiagio[8]进行基坑现场测试时发现，钢板桩凹处和凸处土压力在开挖前一致，但在开挖的过程中两处的差异逐渐产生，因此钢板桩土压力监测必须同时考虑凹处和凸处。Tan等[9]对钢板桩支护的基坑工程进行长期现场监测发现，钢板桩横向土压力分布不均匀。以上学者的实测结果均表明，区别于平面挡墙，钢板桩横截面的波纹形状导致钢板桩横截面凹凸处的土压力差异，由钢板桩截面的几何特征所引起的土压力分布不均不容忽视，但是，这种形状效应的产生机制和影响因素目前尚不明确。

本文采用有限元数值试验方法研究钢板桩主动土压力分布中的截面形状效应。首先，采用ABAQUS有限元分析软件模拟文献[1]所提及的缩尺试验，对比试验数据验证数值模型的有效性。在此基础上，建立典型桩长和截面形状的钢板桩挡墙模型，模拟钢板桩挡墙在不同位移模式和截面形状下的力学响应，并与平板挡墙进行对比，分析钢板桩墙后横向土压力分布的变化规律及影响因素。需要指出的是，钢板桩为柔性桩，钢板桩截面形状直接影响墙体抗弯刚度，进而影响其后土压力的分布。另外，钢板桩的截面形状形成了波纹状的挡土面，这一几何特征本身也将引起土压力重分布。本文主要讨论后者的影响，而综合考虑墙体抗弯刚度和挡土面几何特征影响的研究还有待进一步深入。

2 缩尺试验数值模拟

2.1 缩尺试验简介

Fang等[1]对刚性挡土墙后砂性填土的被动土压力进行了模型试验，所用模型试验箱尺寸(长×宽×高)为200 cm×100 cm×100 cm。刚性墙体分上下2片，下片固定不动，高11.3 cm，上片的位移模式和位移大小通过机械联动装置进行控制，高88.7 cm。墙后填土高61.3 cm，填土为Ottawa砂土，重度为15.5 kN/m3，内摩擦角为30.9°，墙土摩擦角经测定为 19.2°。

如图 1 所示，Fang等[1]共进行了3组不同被动位移模式的试验，即墙体平动(T模式)、绕墙底转动 (RB模式)和绕墙顶转动(RT模式)，墙体运动方向均远离土体。与之相对应的 3 种主动位移模式如图 2 所示，墙体运动方向朝填土方向，但文献[1]未述及主动位移模式的试验成果。

2.2 数值模型

采用ABAQUS程序进行有限元建模，模拟上述缩尺试验以验证数值模型和方法的有效性。模型尺寸及边界条件如图3所示。采用8节点六面体缩减单元，单元数为2340个。土体材料采用Mohr-Coulomb模型，主要参数见表 1。移动挡墙选用程序提供的解析刚体，用单片钢片模拟，在墙体转动点上设置参考点。墙背和土体接触面采用面面接触，接触面法向采用硬接触，切线方向采取罚函数摩擦模型。

图1 被动变位模式示意图Fig.1 Illustration of passive wall movements

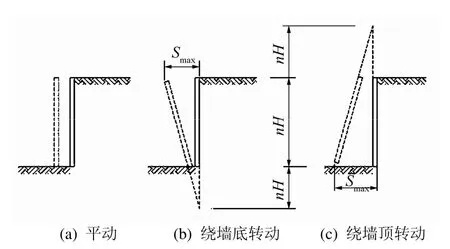
图2 主动变位模式示意图Fig.2 Illustration of active wall movements

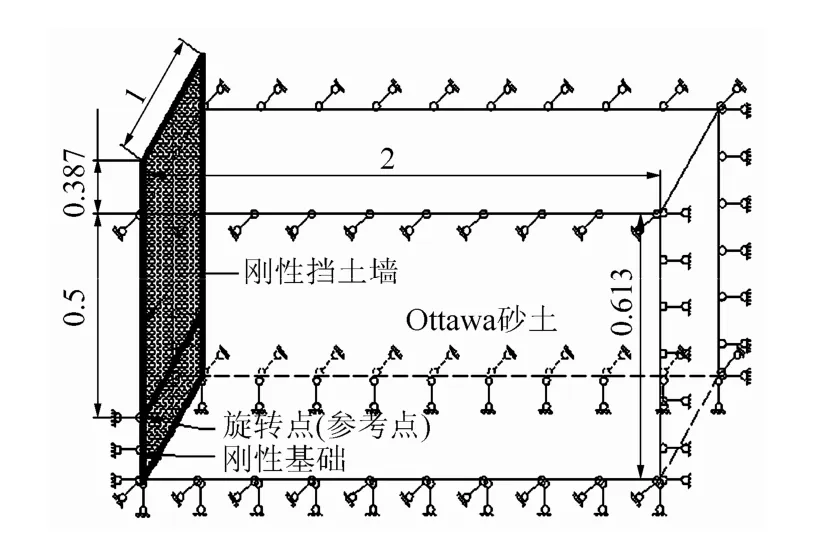
图3 缩尺挡墙试验的数值模型及边界条件（单位：m）Fig.3 Numerical model setup and boundary conditions(unit: m)

表1 模型参数Table1 Model of parameters

2.3 结果对比

数值模拟分析了 3 种不同墙体位移情况下的墙体被动土压力沿填土深度的分布规律(见图1)，数值结果、试验结果与库仑土压力理论计算结果的对比如图 4 所示。

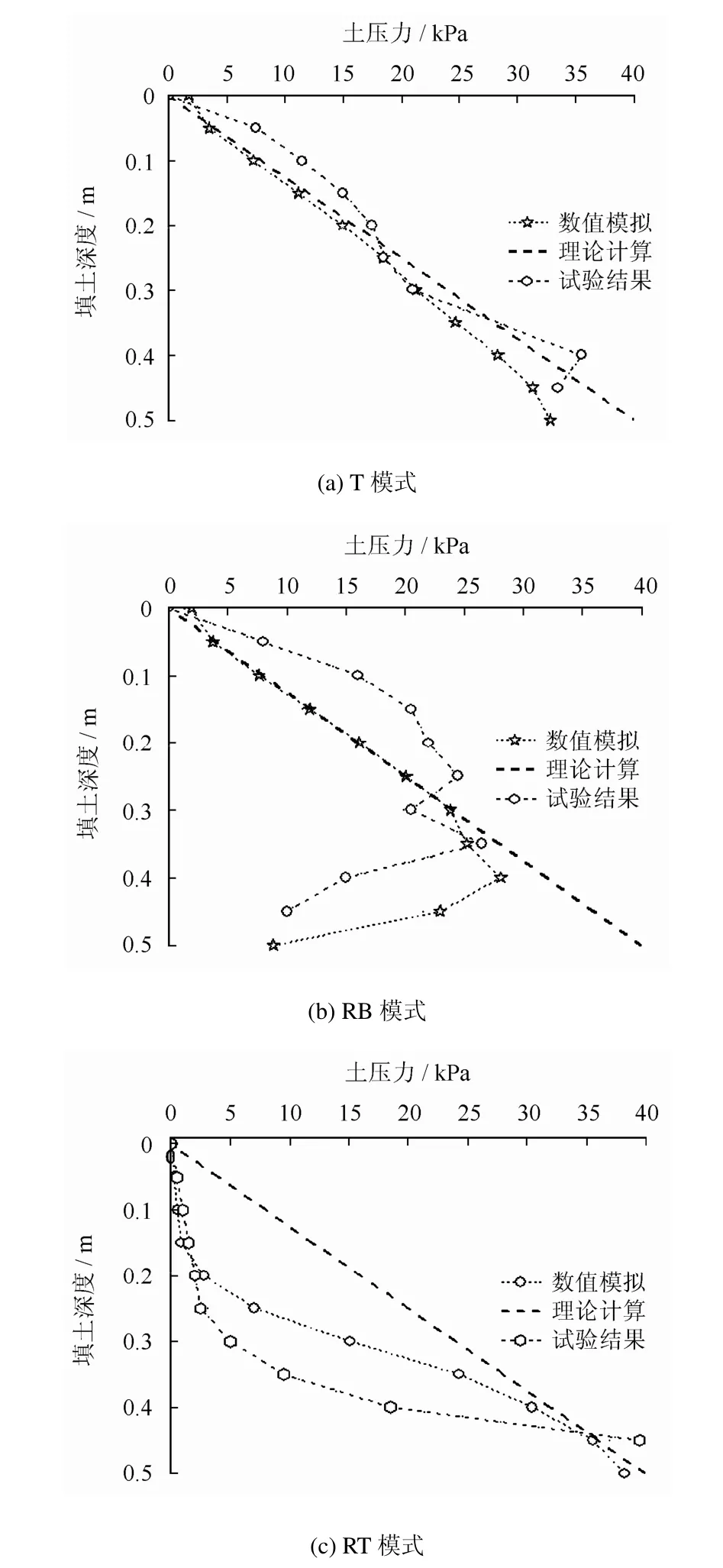
图4 不同位移模式下被动土压力分布Fig.4 Distribution of passive earth pressure in different displacement modes

由图 4 可见，数值计算结果与试验数据吻合较好，土体达到极限被动土压力状态所需的位移量与Brinch-Hansen[10]等多位学者的研究成果一致，为墙高的1%～3%，但小于试验结果（10%～20%墙高），Fang等[2]亦指出所需位移量的试验结果是偏大的。应当指出，填土弹性模量取值对达到被动极限状态所需位移量计算结果影响较大。

3 钢板桩挡墙数值试验

根据上述缩尺试验的工作原理，采用数值试验的方法，通过控制墙体位移，本文研究典型桩长和截面尺寸的钢板桩挡墙在不同位移模式下主动土压力分布情况。

3.1 数值模型建立

选取工程应用较为广泛的NSP-10H型钢板桩进行分析，钢板桩挡墙的三维模型及截面尺寸如图5所示。将钢板桩之间的节点简化为刚性节点。墙体高度取钢板桩的标准长度为12 m，将上述缩尺挡墙模型尺寸放大，建立钢板桩挡墙模型。土体模型长48 m，宽9 m，高36 m，墙体下端设置刚性挡板限制下部土体位移以避免土体溢出。

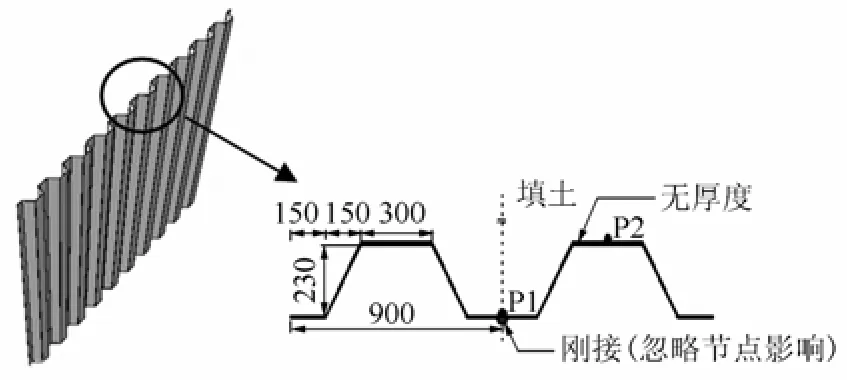
图5 钢板桩挡墙及截面尺寸（单位: mm）Fig.5 Dimensions of hat-type steel sheet pile wall(unit: mm)

土体材料仍然采用Mohr-Coulomb模型，弹性模量 E 取10 MPa，暂不考虑墙土间摩擦的影响，其余参数同表 1。仍然采用8节点六面体缩减单元，单元数目为11097个。

3.2 结果分析与讨论

3.2.1 土压力合力大小与墙体位移的关系

图6 为 3 种位移模式下光滑钢板桩挡墙的水平土压力系数 Kh随位移变化的曲线。定义为单宽墙体所受水平土压力的合力与γH2/2的比值，其中γ 为土体重度；H 为墙体高度。

在 T 模式下，墙体位移达到墙高的4‰时土体达到主动土压力极限状态；钢板桩凹处（图 2中P2点）的Kh值与朗肯理论解接近，约为0.33，但凸处（图 2 的 P1点）的Kh值大于朗肯理论解，约为0.38。在RB模式下，墙体位移达到墙高的1%，仍未见达到主动土压力状态。在RT模式下，达到主动土压力极限状态所需的墙体位移值增至墙高的6‰。在RT模式下，钢板桩墙体凹处和凸处的土压力大小差异不明显，而 RB 模式与 T 模式类似，钢板桩墙体凸处的Kh值大于凹处相应值。需要指出，RT模式和RB模式下的Kh值均大于朗肯理论解。

图6 Kh随位移变化图Fig.6 Variation of Khwith wall displacements

3.2.2 横向主动土压力分布

分别在 4 m 和 8 m填土深度处(即1/3墙高和2/3墙高处)沿钢板桩挡墙宽度方向提取水平土压力，分析不同位移模式下相同深度处水平土压力沿墙体宽度方向的分布情况。为便于对比，将钢板桩挡墙置换为平板挡墙进行平行计算，钢板桩挡墙和平板墙的对比结果如图 7 所示。由图可见，对于平板墙，在同一深度处土压力均匀分布，沿墙体宽度方向的土压力分布曲线为水平直线；对于钢板桩墙体，随着挡墙位移的增加，钢板桩墙后土压力逐渐产生差异，沿墙体宽度方向的土压力分布曲线在平板墙土压力曲线上下变化，变化幅值与位移模式有关。在T模式下，4 m和8 m填土深度处钢板桩挡墙的主动土压力变化幅值分别达到3.9 kPa和8.9 kPa；在RB模式下，不同深度处的变化幅值基本相等，约为5.5 kPa；RT模式与前两种位移模式不同，由于墙体底部位移要远大于顶部，土体在运动过程中，顶部受到相对挤压，即相对被动状态，所以挡墙顶部土体土压力凸处要小于凹处，不同深度处凸处与凹处的土压力差分别为1.2 kPa和7.7 kPa。

图7 钢板桩挡墙和平板挡墙的横向土压力分布Fig.7 Transversal earth pressure distribution against steel sheet pile wall and planar wall

4 形状效应的影响因素

限于篇幅，仅以 T 模式为例，对上述钢板桩主动土压力问题中的形状效应进行影响因素的讨论。

4.1 截面高宽比的影响

钢板桩的截面高宽比β 定义为横截面高度与长度之比。如图 2 所示，NSP-10H型钢板桩单桩的截面长900 mm，高230 mm，其截面高宽比β = 0.255。固定截面长度值，改变钢板桩截面高度，分别取β为0.125、0.255、0.500，建立相应的钢板桩墙体模型，研究截面高宽比对形状效应的影响。需要指出的是，截面高宽比影响钢板桩的抗弯刚度，可能通过影响墙体位移间接影响墙后土体的土压力分布，由于本数值试验采用墙体位移边界控制的方式，不能考虑墙体抗弯刚度的影响，只能单纯考虑挡土面几何特征对土压力分布的直接影响。

图8 为不同填土深度处钢板桩主动土压力随高宽比变化的曲线，图中误差棒的中点（黑色方块）表示凸处与凹处主动土压力的平均值，误差棒的顶端对应钢板桩凸处的土压力值，底端对应钢板桩凹处的土压力值，误差棒的长度钢板桩凹凸处的土压力差，能够直观地代表钢板桩土压力的形状效应大小。随着高宽比增加，平均土压力值变化不大，误差棒长度随之增加，表明形状效应随着高宽比的增加而增强。

图8 截面高宽比对主动土压力的影响Fig.8 Variation of active earth pressure with the ratio of sectional height to width

4.2 弹性模量的影响

图9 为不同填土深度处钢板桩主动土压力随土体弹性模量取值变化的曲线。

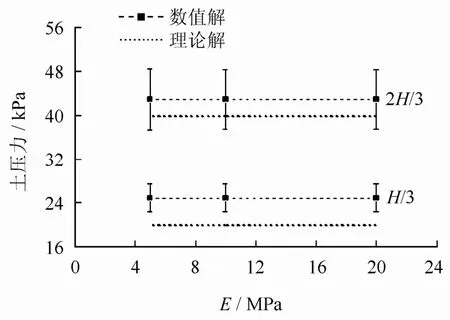
图9 土体弹性模量对主动土压力的影响Fig.9 Variation of active earth pressure with elastic modulus of soil

取NSP-10H型钢板桩（即β取0.255）。误差棒长度基本不变，表明弹性模量对形状效应影响甚微。

4.3 墙土摩擦角的影响

假定土体弹性模量为10 MPa，截面高宽比为0.255，改变墙土之间的摩擦角，不同填土深度处钢板桩主动土压力随墙土间摩擦角取值变化的曲线如图10所示。平均土压力随着墙土摩擦角的增大而减小，跟理论解规律一致，说明随着墙土摩擦角的增大，土压力会随着减小；而误差棒长度基本不变，说明墙土摩擦角对形状效应的影响不明显。

图10 墙土摩擦角对主动土压力的影响Fig.10 Variation of active earth pressure with wall-soil friction angle

5 形状效应产生机制的讨论

图11为填土深度8 m处水平应力云图，墙体凸区（即 a 区）的土体应力大于凹区（即 b 区），出现明显的土拱现象。A-A及B-B截面墙后填土水平位移的计算结果表明，土体在墙体运动过程中产生了相对位移。

图11 土体水平应力云图（单位：kPa）Fig.11 Nephogram of horizontal earth pressure of soil(unit: kPa)

图12为墙后土拱形成示意图。图中，f 为土间摩擦力；Pa为墙后主动土压力；Px为作用在潜在滑裂面的土压力。如图12(a)所示，墙体凸区的水平位移量小于凹区，凸区相对凹区的水平位移方向远离墙体，因此该区受到相邻两侧土体指向墙体的摩擦力，导致如图12(b)虚线所示的应力土拱，使凹区土压力部分转移至凸区，所以墙体凸区所受土压力大于凹区。

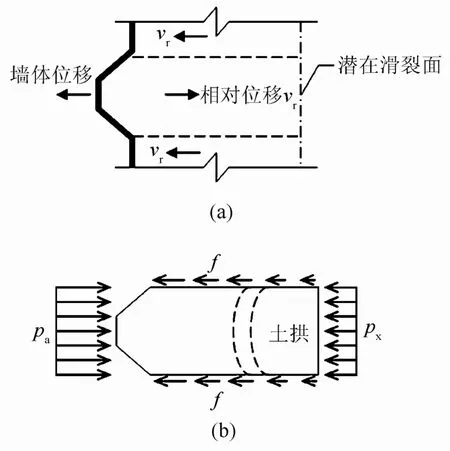
图12 墙后土拱形成示意图Fig.12 Sketch of soil arching

6 结 论

（1）钢板桩的波纹状截面形状影响墙后主动土压力的分布形式，影响程度与位移模式有关。墙体平动和绕墙底转动情况下，钢板桩挡墙凸出部分的主动土压力值大于凹处，但墙体绕墙顶转动情况下差异不明显。

（2）截面高宽比对钢板桩墙体主动土压力分布的形状效应影响较显著，形状效应随着高宽比的增加而增强，弹性模量和墙土摩擦角影响甚微。

（3）钢板桩附近土体的位移差异，导致土体应力拱的产生，是钢板桩土压力问题具有形状效应的原因。

[1]FANG Y S,CHEN T J,WU B F. Passive earth pressure with various wall movements[J]. Journal of Geotechnical Engineering,1994,120(8): 1307－1323.

[2]王元战,李新国,陈楠楠. 挡土墙主动土压力分布与侧压力系数[J]. 岩土力学,2005,26(7): 1019－1022.WANG Yuan-zhan,LI Xin-guo,CHEN Nan-nan. Active earth pressure on a retaining wall and lateral coefficient ofearth pressure[J]. Rock and Soil Mechanics,2005,26(7):1019－1022.

[3]应宏伟,蒋波,谢康和. 考虑土拱效应的挡土墙主动土压力分布[J]. 岩土工程学报,2007,29(5): 717－722.YING Hong-wei,JIANG Bo,XIE Kang-he. Distribution of active earth pressure against retaining walls considering arching effects[J]. Chinese Journal of Geotechnical Engineering,2007,29(5): 717－722.

[4]ZHANG J M,SHAMOTO Y T,ATSU K. Evaluation of earth pressure under any lateral deformation[J]. Soils and Foundations,1998,38(1): 15－33.

[5]陈页开,汪益敏,徐日庆,等. 刚性挡土墙被动土压力数值分析[J]. 岩石力学与工程学报,2004,23(6): 980－988.CHEN Ye-kai,WANG Yi-min,XU Ri-qing,et al.Numerical analysis of passive earth pressure[J]. Chinese Journal of Rock Mechanics and Engineering,2004,23(6): 980－988.

[6]陈页开,汪益敏,徐日庆,等. 刚性挡土墙主动土压力数值分析[J]. 岩石力学与工程学报,2004,23(6): 989－995.CHEN Ye-kai,WANG Yi-min,XU Ri-qing. Numerical analysis of active earth pressure[J]. Chinese Journal of Rock Mechanics and Engineering,2004,23(6): 989－995.

[7]周健,彭述权 樊玲. 刚性挡土墙主动土压力颗粒流模拟[J]. 岩土力学,2008,29(3): 629－638.ZHOU Jian,PENG Shu-quan,FAN Ling. Particle flow simulation of active earth pressure distribution on rigid retaining wall[J]. Rock and Soil Mechanics,2008,29(3):629－638.

[8]DIBIAGIO E. Field instrumentation——A geotechnical tool[M]. Norwegian: Norwegian Geotechnical Institute Pub.,1977.

[9]TAN Y,PAIKOWSKY S G. Performance of sheet pile wall in peat[J]. Journal of Geotechnical and Geoenviromental Engineering 2008,134(4): 445－458.

[10]HANSEN B J. Earth pressure calculation[M]. Copenhagen: Danish Technical Press,1953.