海上风电桩基水平承载力循环衰减二维简化分析

夏华盛，张陈蓉，俞 剑，黄茂松

（1.同济大学 岩土及地下工程教育部重点实验室，上海 200092；2. 同济大学 地下工程与建筑系，上海 200092）

1 引 言

海上风电项目近几年在我国得到了快速的发展，目前海上风电选址主要还是在近海区域，从可行性和经济性方面考虑，桩基础仍是海上风电的首选基础形式，海上风电桩基础长期承受着河流、风机工作荷载等水平循环荷载的作用。针对水平循环受荷桩的问题，学术界开展了大量的工作。较早的有Matlock[1]和Reese等[2]分别对饱和软黏土中钢管桩和砂土中打入桩进行了水平静荷和循环荷载试验，提出了相应的经验p-y曲线公式。近年来高明等[3]开展了饱和砂土中单桩模型试验，在与现场试验对比后，基于土的应力-应变关系给出了水平受荷桩的p-y曲线建议公式。田平等[4]根据试桩资料，提出了黏土中横向周期荷载作用下桩基础的p- y曲线统一法。Rajashree等[5]通过引入与循环次数相关的衰减系数，给出了循环加载后的水平极限承载力公式。Gerber等[6]进行了位移控制的现场水平循环桩试验，发现循环荷载下桩侧的最大土抗力小于对应的静力加载，其认为循环p- y曲线中，桩侧土抗力急剧上升点与前次循环加载幅值相关。

以往的研究大多集中在小数目循环荷载作用下的荷载-位移曲线，但对于海上风电桩基础而言，设计单位更关心的是大数目长期荷载作用下桩基承载力的衰减。本文在商业有限元软件基础上，借鉴Zhou等[7]所建立的软黏土不排水强度弱化模型概念，建立了水平循环受荷桩的有限元数值模拟方法。在与有限元计算结果对比验证基础上，提出了长期循环荷载作用下水平受荷桩基础承载力衰减的简化理论分析方法，从而解决了有限元法在大数目循环荷载计算中的局限性问题，为海上风电桩基础长期安全预测提供了一定的理论依据。

2 不排水弹塑性有限元分析

针对本文中的软黏土不排水条件，土体模型借鉴Zhou等[7]提出的基于修正Tresca屈服准则的理想弹塑性模型概念，通过累积塑性应变考虑循环荷载作用下桩周土体不排水抗剪强度的弱化。在实际的有限元数值模拟过程中，分开计算静力加载与循环加载，静力加载过程中，不考虑土体强度的弱化；循环加载过程中，在加载阶段不考虑土体力学参数的弱化，仅累积其在加载阶段产生的塑性应变，进入卸载阶段，即反向加载的第一个增量步时，根据累积塑性应变对土体的弹性模量以及不排水抗剪强度进行弱化修正。随着循环荷载的持续施加，重复上述工作，不断累积土体产生的塑性应变和进一步修正土体参数，以此类推。本文采用的循环荷载作用下土体弱化衰减模型为

式中：Su为弱化后的土体不排水抗剪强度；Su0为土体初始不排水抗剪强度；Es为弱化后的土体弹性模量；Es0为土体初始弹性模量；δrem为完全重塑土的抗剪强度与初始土体的抗剪强度比值，即土体灵敏度的倒数；ε为循环加载时土体中累积的塑性应变；ε95为应变弱化参数，即土体发生 95%重塑时所对应的累积塑性应变。

对海上风电桩基础中单个桩受水平循环荷载作用进行分析（见图1）。本文有限元模型为水平方向的二维切片，对应的是水平受荷桩深层不考虑三维效应的力学状态。考虑模型以及荷载的对称性，建模选取一半模型。Bransby[8]建议，为消除边界影响，水平受荷桩的土体外边界尺寸取桩半径的25～50倍。据此，本文水平向宽度取30倍桩径，竖向取15倍桩径，采用平面应变8节点四边形单元，有限元模型包括411个单元，1300个节点，网格划分如图2所示，其中红色标示部分为桩身。采用位移控制加载方式施加双向水平循环荷载。桩土界面不考虑相对滑移，单桩截面半径r为0.5 m，土体初始不排水抗剪强度为4.5 kPa，泊松比为0.49，灵敏度取5，即δrem取0.2。考虑刚度指数Es0/Su0、位移幅值yc/r以及应变弱化参数ε95的变化对水平受荷桩的影响，共进行了8组算例计算，循环加载次数均为15次，详细参数见表1。

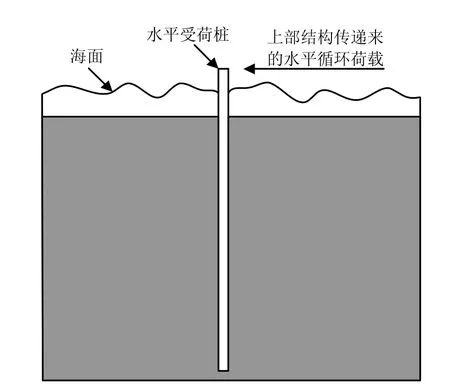
图1 单桩结构示意图Fig.1 Sketch of single pile

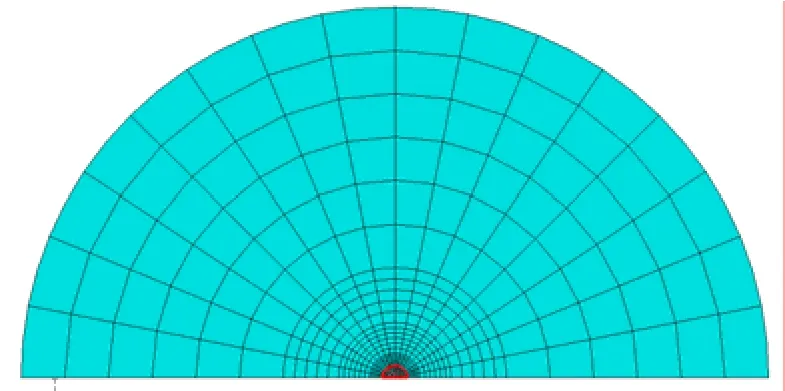
图2 二维有限元网格Fig.2 2D FEM model

表1 各算例参数取值Table1 Parameters for 8 cases

图3为各算例得到的归一化p- y曲线滞回圈。图中，pu为初始状态静力加载的单桩桩侧水平极限抗力。由应变弱化系数ε95定义可知，ε95越大，则土体强度衰减同样程度所需的累积塑性应变越大，土体强度的衰减速度越慢，从图3(a)、3(g)、3(f)、3(h)可以看出，其他条件相同时，ε95越小则土体强度衰减越快，循环后桩侧残余抗力越小。由图3(a)、3(b)可见，虽然土体刚度指数较大时p- y曲线上升速度较快，但对桩的水平抗力影响不大。

由于本文有限元计算循环荷载是位移控制加载方式，在其他条件相同时，位移幅值越大，所对应的累积塑性剪应变越大，土体强度的衰减也就越多。由图3(a、3(e)、3(c)、3(g)可见，位移加载幅值较小时土体强度下降较慢，而位移加载幅值较大时，土体强度迅速下降并趋于稳定。

图4为循环加载后进行静力加载得到的p- y曲线与初始静力加载p- y曲线对比图。由图可见，当加载位移幅值较大时，由于桩周大部分土体进入塑性区并继续发展，累积的塑性剪应变较大，因此桩侧水平抗力急剧下降，并且趋于0.2倍的初始极限抗力；当加载幅值较小时，由于桩周较多土体尚未进入塑性状态，累积的塑性剪应变较少，水平抗力下降不明显。此外，应变弱化系数对桩侧循环后的水平抗力影响，加载幅值较大时影响相对更小。当加载幅值较大时，由于累积塑性应变较大，桩侧水平抗力在本文循环次数下已开始趋于稳定。

图3 水平循环受荷单桩滞回曲线（本图纵坐标由pc/pu修改为p/pu）Fig.3 Hysteretic curves for a laterally cyclic loaded pile

图4 初始静力加载和循环后静力加载p-y曲线对比Fig.4 Comparison between p-y curves on for monotonic load and post monotonic load

3 二维简化分析方法

静力加载时，Gerolymos等[9]建议采用p- y曲线形式为

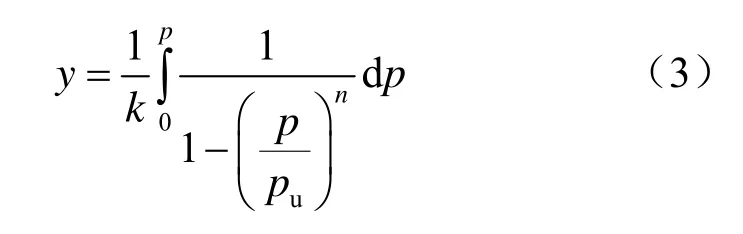
式中：k为桩侧切线模量；pu为桩侧极限抗力；n为p- y曲线形态控制参数，取值范围为 0～∞，当n＞10时p- y曲线近似为二折线。

桩侧切线模量k的确定，本文借鉴 Baguelin等[10]提出的模型，将桩周土体区域分为内外两个圆环，外层圆环半径范围为 r1→R，内层圆环半径范围为 r→r1（r为桩的半径）。桩侧外层圆环区域土体处于弹性状态，力学特性不受桩的影响，弹性模量为Es0，内层圆环区域因桩受循环荷载作用，土体弹性模量弱化为Es。针对软黏土不排水情况，土体泊松比v=0.5，根据Baguelin等[10]的理论推导得到单桩的弹性位移y和水平抗力p之间的关系为

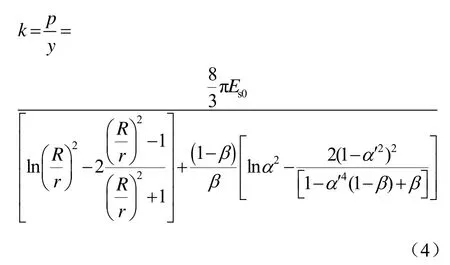
式中：v为土体泊松比；β=Es/Es0；α=r1/r；α′=1/α。

由 Bransby[8]的建议，得到R/r取值在 25～50之间。式（4）得到R/r足够大时对计算结果没有影响，为与有限元计算建模一致，本文采用R/r=30。Klar[11]通过极限分析认为，水平受荷桩取α=2.85较为合理，并得到桩侧塑性位移与扰动区域土体塑性应变关系为

桩侧土体的塑性衰减仍采用与有限元一样的表达式。在计算中实现桩侧p- y曲线的弱化，需要将位移y区分为弹性位移和塑性位移。具体为：加载后对式（2）、（5）同时进行迭代运算，可得到满足以上两个式子的塑性位移和相对应的塑性应变。

水平循环受荷桩的简化计算分为两个阶段：（1）加载时采用的p- y曲线不考虑土体弹性模量以及不排水抗剪强度的弱化，仅累积其在加载时产生的塑性应变ε。（2）当一次加载结束后根据前期累积的塑性应变ε对下一次加载时土体的弹性模量以及不排水抗剪强度进行弱化修正后，进行弹性卸载并用弱化后的参数进行再次加载计算。为与有限元数值模拟对应，简化方法的计算参数取 Es0/Su0=500，ε95=30，δrem=0.2。

图5为通过调整式（3）的形态参数n，得到与有限元较为接近的p- y曲线，确定了本文简化方法p- y曲线的表达式。在此基础上，分别采用简化理论方法和有限元数值模拟进行了等荷载幅值条件下的水平循环受荷桩的计算，在循环荷载后对单桩施加静力荷载，得到其循环后的桩侧极限抗力，计算结果对比如图6所示。图中，pc为水平循环荷载幅值；pu为静载条件下桩侧的极限抗力；pus为循环加载结束后再次进行静力加载得到的桩侧极限抗力。有限元计算对应的循环荷载次数分别为5、10、50、100次，共进行了3组不同的循环荷载幅值条件下的分析，分别为pc/pu=0.5、0.6、0.7。

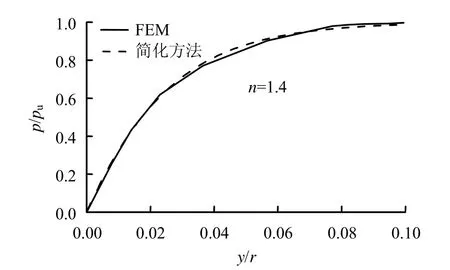
图5 静力加载p-y曲线Fig.5 p-y curves for monotonic load

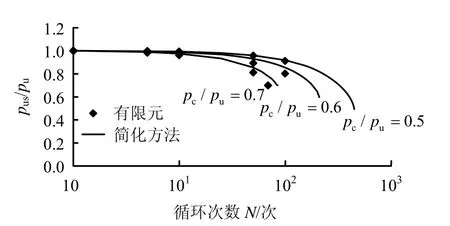
图6 循环次数和残余桩侧抗力的关系Fig.6 Relationships between residual lateral capacity and cycle numbers

由图6可见，针对不同的循环荷载幅值以及循环荷载加载次数，对循环荷载后静载条件下桩侧极限抗力的弱化预测，有限元数值模拟以及简化方法给出的结果较为符合。如 pc/pu=0.7的情况，有限元计算结果为 69次循环后桩出现了破坏，而简化方法则为 85次，所谓破坏即指由于桩侧土体的弱化，桩侧极限抗力已小于循环荷载加载幅值，水平受荷桩已无法承受对应的循环荷载。通过对比3种循环荷载幅值条件下桩侧极限抗力衰减与循环荷载次数的关系曲线发现，随着水平循环荷载幅值的增加，桩所能承受的循环荷载次数在逐渐减少。这主要有两个原因，（1）荷载幅值的增加使得土体累积的塑性应变相应增大，导致土体加速弱化；（2）循环荷载幅值的增加使得破坏时所对应的桩侧极限抗力同比例增加。

鉴于有限元数值模拟时间成本大，难以进行长期大数目循环荷载次数下桩侧水平极限抗力的衰减预测，本文采用提出的简化理论分析方法计算，得到了一系列循环荷载幅值比较小的情况下桩侧极限抗力衰减与循环荷载次数的关系曲线，如图 7所示。由图可见，当 pc/pu＞0.2时，随着循环次数的增加，桩均出现了破坏；当 pc/pu≤0.2时，循环荷载下桩的累积位移会不断增加，但从承载能力角度来看，桩却趋于稳定，没有发生破坏。这是由于本文计算中δrem取值为0.2，其定义为完全重塑土的抗剪强度与初始土体的抗剪强度比值，因此，当循环荷载幅值小于δrem时，桩侧土体即使由于循环荷载作用衰减完全弱化，桩侧最小极限抗力也会大于循环加载幅值，不同的只是随着水平循环荷载幅值减小，桩侧极限抗力的衰减速度会越慢，如pc/ pu=0.05的情况，循环次数为 105次时，极限承载力为静力加载极限承载力的82%。

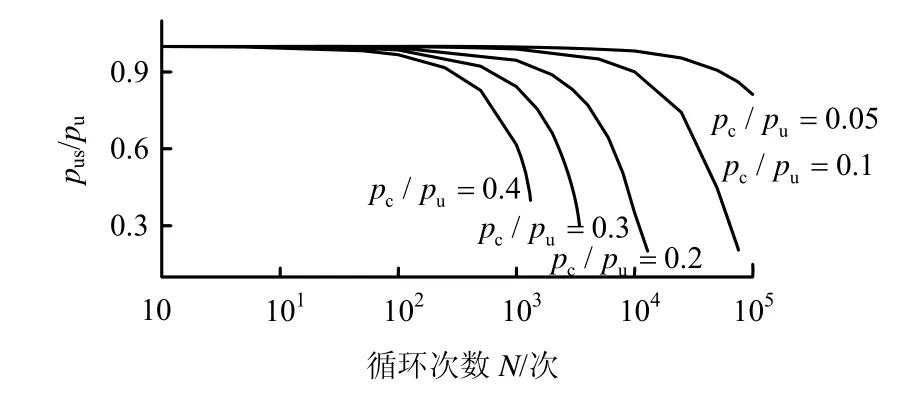
图7 循环次数和残余桩侧抗力的关系Fig.7 Relationships between residual lateral capacity and cycle numbers

4 结 语

通过塑性应变的积累考虑土体不排水强度的弱化，模拟软黏土中单桩受水平循环荷载时桩侧极限抗力的衰减弱化特性。有限元分析表明，当采用等幅位移加载方式施加水平循环荷载时，土体刚度指数对于桩侧水平抗力衰减影响不大，应变弱化系数对桩侧水平抗力衰减的影响在位移加载幅值较小时影响更大。二维简化理论分析发现，当采用等幅荷载加载方式施加水平循环荷载时，当荷载加载幅值小于等于0.2倍初始桩侧抗力时，单桩在长期水平循环荷载作用下会趋于稳定，不会发生破坏，0.2倍系数对应的是本文算例采用的土体灵敏度的倒数。在长期水平循环荷载作用下，桩侧抗力能否趋于稳定，以及所能承受的不致破坏的最大循环荷载次数与循环荷载的加载幅值以及桩侧土体的力学特性均有联系。

在海上风电设计中，必须对选址区域风电桩基所承受的长期循环荷载以及土体的力学特性进行关注和优化分析，以保证海上风电的长期安全可靠性。鉴于本文的分析仅仅是二维切片深层模型的探讨，没有进入水平受荷桩的三维分析，对桩长、桩径等设计参数还未涉及，也是后续工作的方向。

[1]MATLOCK H. Correlation for design of laterally loaded pile in soft clay[C]//Proceedings of 2nd Offshore Technology Conference. Houston: [s. n.],1970: 577－594.

[2]REESE L C,COX W R,KOOP F D. Analysis of laterally loaded piles in sand[C]//Offshore Technology in Civil Engineering: Hall of Fame Papers from the Early Years.Houston: [s. n.],1974: 473－483.

[3]高明,陈锦珍,郑国芳,等. 桩在侧向静、动、循环荷载下的性能研究及 p-y曲线建议公式[J]. 海洋工程,1988,6(3): 34－43.GAO Ming,CHEN Jin-zhen,ZHENG Guo-fang,et al.Studies on behavior of lateral loaded piles under static,dynamic and cyclic loadings and proposal of p-y curve formulation[J]. The Ocean Engineering,1988,6(3): 34－43.

[4]田平,王惠初. 黏土中横向周期性荷载桩的 p-y曲线统一法[J]. 河海大学学报,1993,21(1): 9－14.TIAN Ping,WANG Hui-chu. A unified method of p-y curves for laterally and periodically loaded piles in clay[J].Journal of Hohai University,1993,21(1): 9－14.

[5]RAJASHREE S S,SUNDARAVADIVELU R. Degradation model for one-way cyclic lateral load on piles in soft clay[J]. Computers and Geotechnics,1996,19(4):289－300.

[6]GERBER T M,ROLLINS K M. Cyclic p-y curves for a pile in cohesive soil[C]//Proceedings of the Geotechnical Earthquake Engineering and Soil Dynamics－IV.California: Geotechnical Special Publication,2008: 1－10.

[7]ZHOU H,RANDOLPH M F. Computational techniques and shear band development for cylinder and spherical penetrometers in strain-softening clay[J]. InternationalJournal of Geomechanics,2007,7(4): 287－295.

[8]BRANSBY M F. Selection of p-y curves for the design of single laterally loaded piles[J]. International Journal for Numerical and Analytical Methods in Geomechanics,1999,23: 1909－1926.

[9]GEROLYMOS N,GAZETAS G. Constitutive model for 1-D cyclic soil behavior applied to seismic analysis of layered deposits[J]. Soils and Foundations,2005,45(3):147－159.

[10]BAGUELIN F,FRANK R,SAID Y H.Theoretical study of lateral reaction mechanism of piles[J]. Geotechnique,1977,27(3): 405－434.

[11]KLAR A. Upper bound for cylinder movement using“elastic” fields and its possible applicaton to pile deformation analysis[J]. International Journal of Geomechanics,2008,8(2): 162－167.