非饱和渗流Richards方程数值求解的欠松弛方法

陈 曦，于玉贞，程勇刚

（1. 北京交通大学 土木建筑工程学院，北京 100044；2. 清华大学 水沙科学与水利水电工程国家重点实验室，北京 100084;3. 武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072）

1 引 言

非饱和土渗流理论是非饱和土力学理论体系的一个重要组成部分，Richards方程是非饱和土渗流理论的基本方程，在土石坝渗流、污染物传输、冻土渗流相变和边坡稳定性分析等领域有着广泛的应用，例如，污染物在饱和与非饱和土中迁移的基本方程可以通过 Richards方程和对流扩散方程导出[1]。对于渗流引起的边坡失稳问题，目前主要采用渗流与变形非耦合的分析方法[2]，研究结果表明，非饱和渗流场和侵润面的计算对边坡的稳定性和安全系数等结果具有显著的影响[3－4]，开展Richards方程数值求解方法的研究具有十分重要的意义。

针对 Richards方程数值求解过程中的各种问题，研究人员已经开展了相关的研究，如吴梦喜等[5]研究了非饱和渗流求解过程中的数值弥散现象（即土体饱和度比较低处孔隙负压计算的结果分布规律较乱，出现与实际物理表现不符的现象），为消除这一现象提出了变坐标的特征有限元法。Richards方程空间离散和时间差分后，一般可采用非线性迭代方法来求解每一时间步所对应的方程，常用的方法有 Picard迭代法和 Newton迭代法，Mehl[6]通过比较Picard迭代法和Newton迭代法，得出与Newton迭代法相比，Picard的结论通常更加简单有效。非饱和土的水力传导系数（即渗透系数）具有较强的非线性特征，是导致常规Richards有限元方程的收敛性较差的主要原因之一，一些研究人员尝试采用变量变换方法来改善Richards有限元方程的求解性能。Williams等[7]认为，非饱和渗流变量（如压力水头）在较小空间和较短时间范围内的快速变化，是引起Richards有限元方程非线性较强和求解困难的主要原因，基于常规的方程格式和求解方法未必有效，建议针对变量进行变换来改善Richards有限元方程的非线性和收敛性，并研究不同的变换方法。Miller等[8]提出基于误差控制的自适应策略，将其同时应用于Richards方程的空间离散和时间差分，提出空间和时间自适应求解方案。

在Richards方程的数值求解过程中，某些参数尤其是水力传导系数的计算，需要采用欠松弛（under-relaxation）法,不同的欠松弛法对非饱和渗流的数值求解精度和计算效率具有显著的影响[9－10]。变量变换技术的性能也是依赖于欠松弛方法[11]，从基本变量进行欠松弛方法的研究尤为重要。本文通过数值实例指出了现有欠松弛法的局限性，提出一种新的混合欠松弛方法，并对其实用性和可靠性进行了验证。

2 非饱和渗流Richards有限元方程

经过多年的发展，非饱和土渗流Richards方程已衍生出3种基本格式，即压力水头格式（h-form）、混合格式（mixed form）和体积含水率格式（θ-form）。尽管混合格式的Richards方程被证实具有严格质量守恒的特性，压力水头格式的Richards方程在实际工程中的应用仍十分广泛。

混合格式的Richards方程表达式为

式中：θ 为体积含水率，θ = nSf，n为多孔介质的孔隙率，Sf为流体的饱和度；s为源汇项；K =KsKr(Θ)，Kr(Θ)为相对渗透张量，为有效饱和度Θ的函数；Ks为饱和渗透系数张量；(x,t)∈Ω ×(0,T ]。非饱和渗流数值分析通常采用 Mualem[12]定义的水力传导系数，即

式中：ks为饱和水力传导系数；有效饱和度或标准化含水率Θ可由van Genuchten[13]定义的土-水特征曲线计算，即

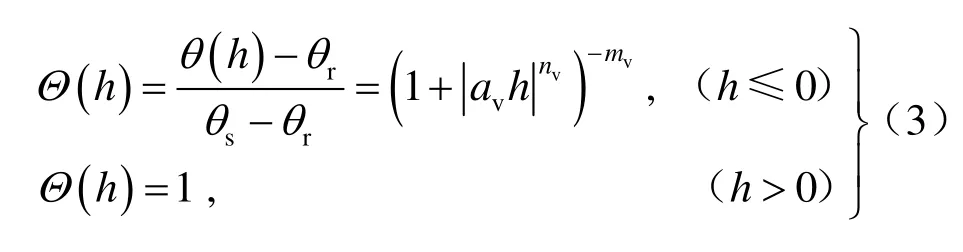
式中：h为压力水头；θ、θs、θr分别为体积含水率、饱和含水率和残余含水率；av、nv、mv分别为经验系数，mv通常简化为mv= 1-1/nv。

根据比存储量概念（即土-水特征曲线的导数）：

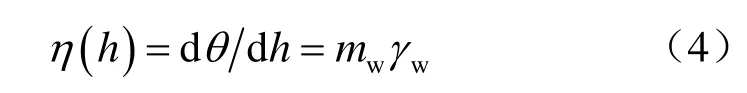
式中：mw为土-水特征曲线的斜率；γw为水的单位重度。

利用式（4），将式（1）表示为h-form的Richards方程，即

对式（5）应用Galerkin加权残量法，经过空间离散和时间差分后可得h-form的Richards有限元方程：

式中：下标n表示时间步指标；M、C分别为等价质量矩阵和水力传导特征矩阵，由相应单元矩阵Me、Ce组装而成：

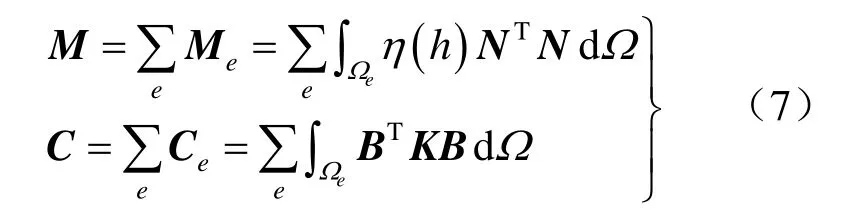
式中： N、B分别为形函数矩阵及其导数矩阵。右端矢量为b=s+g+f，其中：

式中：z为节点高程矢量；n为边界单位法线矢量。

式（6）的增量迭代形式又称为修正Picard（这里记为mPicard）迭代，表示如下：

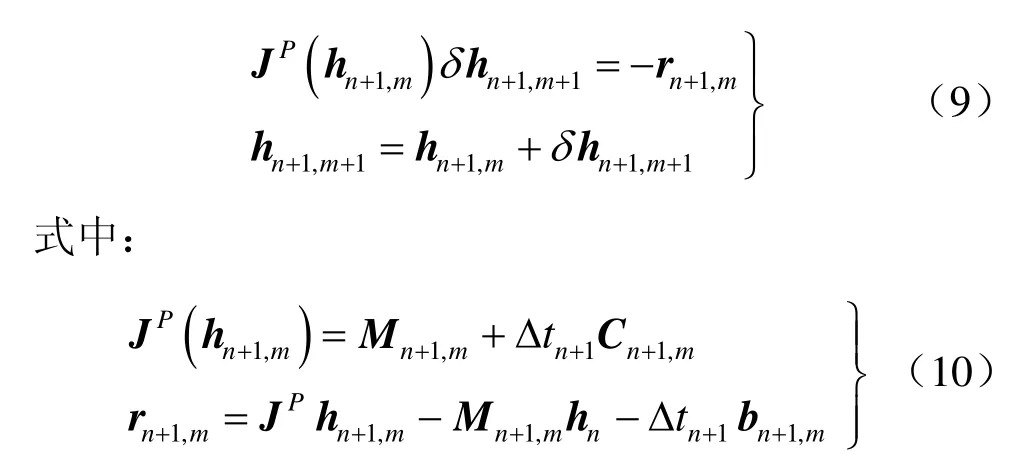
当式（9）中第一式中 JP替换为准确雅克比矩阵（JN= J时），mPicard迭代法成为Newton迭代法。

3 非线性迭代收敛震荡与欠松弛方法

在迭代过程中，式（2）中第一式水力传导系数的计算需要输入适当的压力水头：

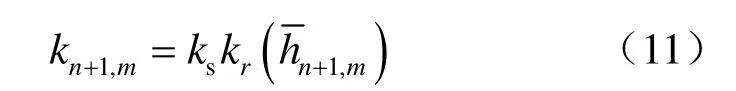
根据Tan等[9]的研究，当=hn+1,m时，水力传导系数采用当前时间步、当前迭代步的压力水头进行计算，这种未使用欠松弛的方法记为UR0。然而，直接使用当前迭代步的压力水头来计算水力传导系数可能会引起如图 1所示迭代收敛震荡。Phoon等[10]对这种迭代收敛震荡现象进行了分析，认为上述震荡现象是由水力传导系数相对渗流量计算不协调造成。为了降低迭代收敛震荡对求解精度和计算效率的影响，可采用适当的欠松弛方法。当采用前一时间步结束时的压力水头与当前时间步当前迭代步的压力水头的均值来计算水力传导系数时，即

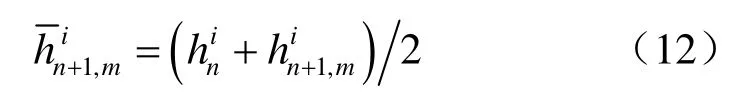
这种方法称为UR1方法。由于UR1方案简单有效，商业软件GeoStudio中的SEEP/W模块采用了这一方法。Tan等[9]和 Phoon等[10]分别研究了 3种不同的欠松弛方法，即上述的UR0、UR1和下面的UR2方法：

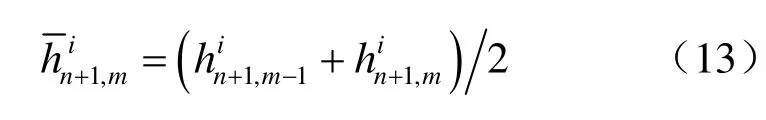
这里，UR2方法采用当前时间步最近两次迭代步的压力水头的均值来计算水力传导系数。他们通过一维算例得出“UR2方案在网格较粗的情况下能够给出更加精确的压力水头场，而UR1尽管收敛较快，结果却明显偏离正确解”的结论[9-10]。采用同一算例对1 m厚、初始条件为干燥的土层进行有表面雨水入渗的模拟，具体参数见章节 5.1算例。图 1给出 10单元网格一维非饱和渗流的计算结果，显示了 UR1只需少量迭代步数便可达到收敛，但其收敛值（约为-8.0 m）明显偏离了解析解-0.0216 m。UR2和UR0都能收敛到较为精确的解，但UR2相对 UR0需要较少的迭代步数。图 1的局部放大图显示UR2和UR0欠松弛方法作用下迭代法仍存在围绕正确解的迭代收敛震荡现象，正是由于这种迭代收敛震荡导致了Picard或Newton等非线性迭代方法收敛缓慢和数值求解精度降低等问题。

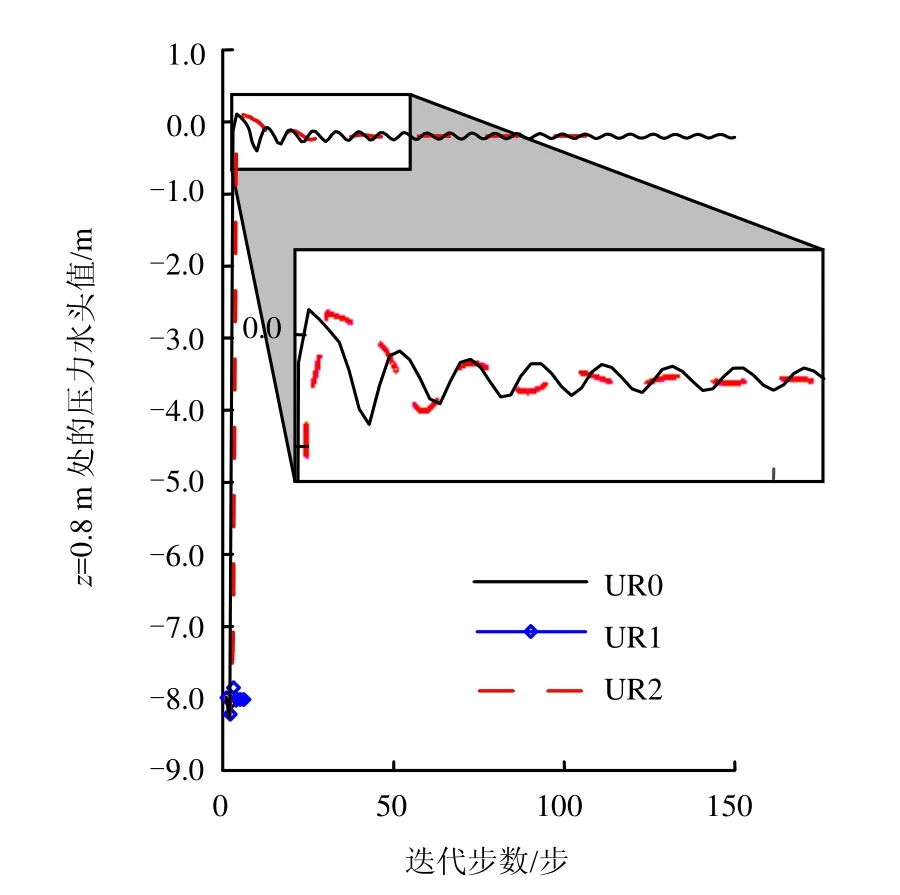
图1 3种欠弛松方法作用下Picard方法的迭代收敛行为Fig.1 Convergence behaviors of Picard iteration

4 一种混合欠松弛方法

理论上，上述的欠松弛方法可以统一在下面的广义欠松弛方法的框架内，其表达形式为

式（14）表示水力传导系数计算所采用的压力水头为前一时间步结束时的压力水头和当前时间步所有迭代步已知压力水头的线性组合。很明显，采用广义欠松弛方法来构造近似压力水头主要存在以下两个问题：①随着迭代步数的增加，广义欠松弛方法需要存储前面所有迭代步的压力水头；②公式右端各项压力水头的系数很难确定。针对上述问题，可只保留式（14）右端的2～3项。根据对图1中欠松弛方法的观察，做出如下推测：①前一时间步结束时的压力水头hn在欠松弛迭代法中具有阻尼收敛震荡的作用，如UR1；②为了获得较为精确的收敛结果，应尽可能保留最近的迭代结果，即hn+1,m，如UR0和UR2；③增加前几步迭代的结果也有阻尼收敛震荡的作用，如UR2中的hn+1,m-1，但阻尼效果较弱。

基于上面的理论分析、数值观察和推测，提出一种混合欠松弛方法，即

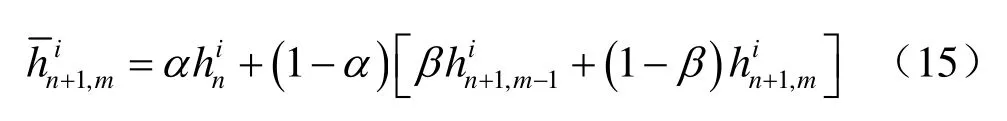
式中：α∈[0,1]和β∈[0,1]为欠松弛经验参数，由于hn的阻尼作用，α也称为阻尼系数。

此短项欠松弛法可以看作 UR0、UR1和 UR2的混合方法，记为 mUR(α,β)，而 UR0、UR1和UR2法也可以看作是这种混合欠松弛方法的特例，即当α= 0，β= 0，mUR退化为UR0；当α= 0.5，β= 0，mUR退化为UR1；当α= 0，β= 0.5，mUR成为UR2。根据前面的Richards有限元方程和欠松弛方法编制了非饱和渗流计算程序和可视化界面，通过具体实例指出现有欠松弛方法的局限性，并对所提出的混合欠松弛方法的优越性进行验证。

5 数值评价

5.1 一维均质土的非饱和渗流

算例1. 对一维均质土的非饱和非稳态渗流问题进行模拟[10]。模型饱和体积含水率θs和残余体积含水率θr分别为0.363 和0.186，van Genuchten模型中的参数av、nv分别为1 m-1和1.53，饱和渗透系数为ks= 1×106m/s。模型中，1 m厚土层划分为10单元有限元网格（即Δz = 0.1 m）。在均匀干燥的初始条件下（设为h(z,0) = -8.0 m），上表面有水逐渐渗入时的边界条件设为h(0,t) = -8.0 m，h(1.0,t)=0.0。计算t = 46800 s的压力水头分布时，随网格和时间步长逐渐加密，压力水头逐渐收敛，如图2所示。采用UR2欠松弛方法，当网格密度达到100单元时，压力水头分布已经足够精确，与1000个单元网格对应的曲线非常接近。采用1000个单元时，在0.8 m的位置处，压力水头的计算结果为-0.0208 m，接近解析解为-0.0216 m[10]。

仍采用10单元有限元网格，令混合欠松弛方法中参数。β取固定值 0.5，观察α变化对求解精度和效率的影响。图3为mUR(α,0.5)作用下mPicard迭代法在t = 46800 s时的压力水头分布。这里，mUR(0,0.5)变为UR2欠松弛方法，其结果用十字标记表示。由图可见，随着α的增大，压力水头分布逐渐偏离红色虚线表示的密网格解。当α= 0.5时，压力水头分布与三角形标记表示的 UR1方法给出的结果几乎一致，意味着β参数影响甚微。

图2 压力水头分布随网格和时间步长加密的收敛情况Fig.2 Convergence of pressure head distribution with the refinement of finite element mesh and time step

图3 mUR中参数α 对压力水头分布计算精度的影响Fig.3 Effects of α in mUR on solution accuracy

通过上述分析可知，当网格划分较粗时，α应足够小（例如α∈(0,0.01]）才可确保收敛到较为精确的解。相应地，将 mUR(α,0.5)作用下 mPicard迭代法在z = 0.8 m高程处解的迭代收敛过程绘制在图4中，这里选取部分具有代表性的α值。有趣的是，随着α值的增加，迭代求解的精度逐渐下降，mPicard迭代求解的速度却在增加，且当α值足够小时，计算精度下降不是很明显。但α= 0.01与α=0（即UR2方法）相比，mPicard所需的迭代数分别为68步和112步，迭代步减少约为40%；当α较大时，迭代收敛尽管很快，结果却偏离正确解较大，这一点与UR1方法相似，印证了前面的推测①的合理性，证实了混合欠松弛方法 mUR(α,β)中 hn对迭代震荡具有较好的阻尼作用，且此算例中参数α益取一个较小的值。

图4 mUR中参数α 对mPicard迭代性能的影响Fig.4 Effects of α in mUR on the performance of mPicard

确定 mUR(α,β)中的参数α后（设定为α=0.01），还需要进一步研究和评价β变化对求解精度和计算效率的影响。根据数值结果，mUR(α,β)中β变化时所得到的压力水头分布与图3中α= 0.01对应的曲线基本上一致（因此这里没有绘出），表明此算例中求解精度主要由α控制。图5显示β参数对mPicard的计算性能的影响。由图可见，与UR2的112步（图中红色虚线标定）相比，β取0.5以下一定范围的值都可以导致约 50%的迭代步数节省，表明混合欠松弛方法在保证精度的同时，可有效提高迭代法的计算效率。

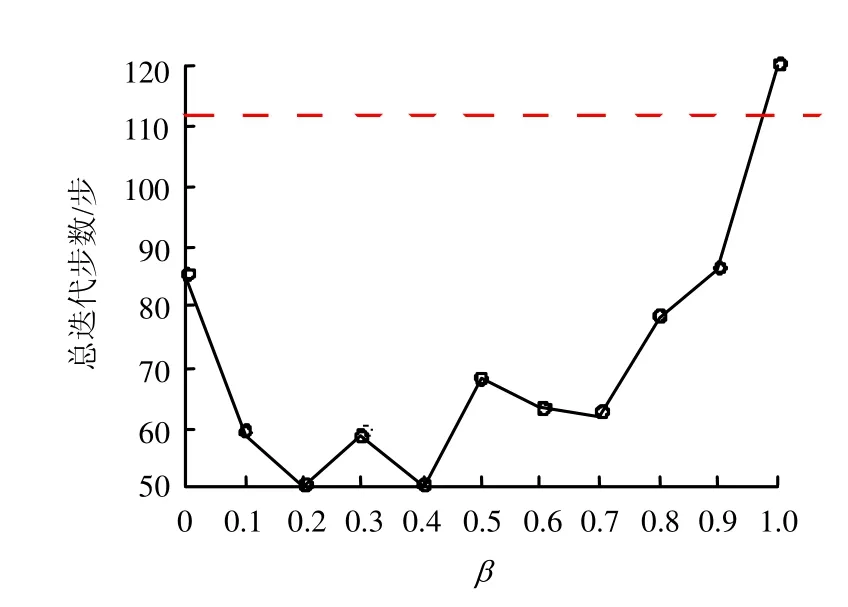
图5 mUR中参数 β 对mPicard迭代性能的影响Fig.5 Effect of β in mUR on the performance of mPicard

5.2 二维非均质坝体的非饱和渗流

算例2. 参照于玉贞等的文献[4]，坝体和2层堤基的非饱和土参数分别为：堤身土，(θs,θr,av,nv,ks) = (0.441,0.106,1.9 m-1，1.31,6.7×10-7m/s)；堤基黏土层：(θs,θr,av,nv,ks) = (0.490,0.123,0.8 m-1,1.09,1.8×10-7m/s)；堤基砂土层：(θs,θr,av,nv,ks) =(0.411,0.049,7.5 m-1,1.89,2×10-5m/s)。采用 3 组有限元网格（记为A，B和C），分别含有160、320和2008个4节点四边形流体单元。对于最密的网格划分C，时间步长设为Δt = 900 s（288个时间步），为了提高计算效率，这里采用稀疏格式的对称连续超松弛（SSOR）预处理的共轭梯度（CG）迭代法并结合 Eisenstat技巧[14]来求解每一非线性迭代步对称正定线性方程组。坝体一侧初始水位为 17 m标高，另一侧保持恒定水位为10 m标高，在此水位差条件下达稳态渗流。以此稳态渗流状态为初始条件，坝体一侧水位从17 m标高处以1 m d-1的速度开始下降，经过3 d，水位下降3 m后坝体内非稳态渗流压力水头分布如图6所示。

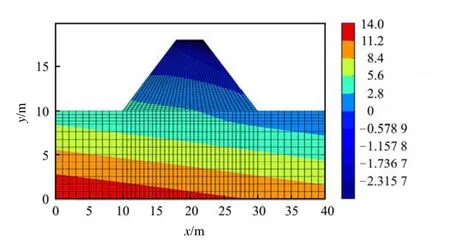
图6 水位下降3 m后的压力水头分布（单位：m）Fig.6 Distribution of pressure head after 3 m water level drawdown (unit: m)

图6根据网格C和UR1方法求出的非稳态渗流压力水头场，在网格C条件下，采用UR1、UR2和 mUR几种欠松弛方法所得到的压力水头分布基本一致，因此，可将其用于评价粗网格的计算精度。图7为根据网格A和网格B所获得的0压力水头线，时间步长分别设为Δt = 10800 s（24个时间步）和Δt = 5400 s（48个时间步）。 由图可见，对于2个粗网格，蓝色实线对应 UR1方法所获得的计算精度（其累计迭代数分别为3612和8207）要明显好于红色实线表示的UR2方法（其累计迭代数分别为8579和18179），而且随着网格加密，UR1的计算结果较快收敛于正确解（这里指虚线对应的加密网格获得的0压力水头线）。需要强调的是，比较上述两个算例可知，欠松弛方法的性能会因问题不同而呈现显著差别，Tan等[9]和 Phoon等[10]的数值研究并不全面。

参照UR1方法（即β= 0），固定β= 0，α从0.6变化到1.0，计算得到的0压力水头线与图7中UR1给出的0压力水头线基本一致，表明上述参数情况下计算精度变化甚微。图8为相应的累计迭代数变化曲线，括号中的数字为mPicard未收敛的累计时间步数，这里 mPicard采用的收敛允许值为1×10-5，最大允许迭代数为500。如图所示，保持β=0，α从0.5变化到1.0时，累计迭代数基本呈下降趋势，表明在这种情况下，采用较大的α可以显著减少计算量。对于网格 A和网格 B，mUR(1.0,0)作用下的累计迭代数分别是2772和5770，与UR1作用下的累计迭代数（分别为3612和8207）相比，计算量分别节省了23%和30%。

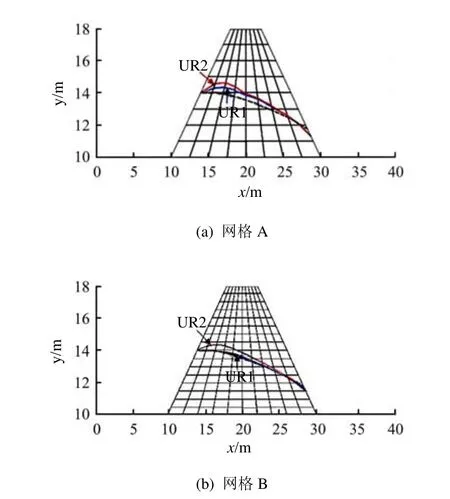
图7 水位下降3 m后的0压力水头线Fig.7 The 0 pressure head curves after 3 m water level

图8 mUR中参数 α 对计算量的影响Fig.8 Effects of α in mUR on computing cost

6 结 论

（1）非饱和渗流数值求解时，水力传导系数相对渗流量计算不协调会造成迭代法收敛震荡，欠松弛方法的主要作用是对这种迭代震荡施加一种阻尼。通过数值试验可知，对于迭代法的收敛震荡，前一时间步结束时的压力水头hn的阻尼抑制效果明显。

（2）算例演示了现有两种常用欠松弛方法计算性能的显著差异，表明单一欠松弛方法所存在的局限性。在一维粗网格入渗算例中，UR1方法收敛较快，但收敛结果却偏离正确解较大，UR2方法作用下非线性迭代法可收敛到较为正确的解，但收敛速度相对较慢。二维堤坝渗流算例与一维入渗算例结论不同，UR1方法收敛较快且计算精度也明显好于UR2。

（3）基于广义欠松弛方法，发展出的混合欠松弛方法mUR可以看作是UR1和UR2的泛化方法。通过 mUR(α,β)中的系数可调整阻尼程度和欠松弛程度。数值试验表明文中所提出的混合欠松弛方法克服了单一欠松弛方法的局限，具有更好的适用性和计算性能。

[1]李锡夔. 饱和－非饱和土壤中污染物运移过程的数值模拟[J]. 力学学报,1998,30(3): 321－331.LI Xi-kui. Numerical modelling of pollutant transport in unsaturated/saturated soils[J]. Acta Mechanica Sinica,1998,30(3): 321－332.

[2]陈曦,刘春杰. 逐步完善的非饱和土边坡稳定性有限元分析方法[J]. 岩土工程学报,2011,33(增刊1): 380－384.CHEN Xi,LIU Chun-jie. Staged development of finite element methods for stability of unsaturated soil slopes[J].Chinese Journal of Geotechnical Engineering,2011,33(Supp. 1): 380－384.

[3]黄润秋,戚国庆. 非饱和渗流基质吸力对边坡稳定性的影响[J]. 工程地质学报,2002,10(4): 343－348.HUANG Run-qiu,QI Guo-qing. The effect of unsaturated soil suction on slope stability[J]. Journal of Engineering Geology,2002,10(4): 343－348.

[4]于玉贞,林鸿州，李荣建,等. 非稳定渗流条件下非饱和土边坡稳定分析[J]. 岩土力学,2008,29(11): 2892－2898.YU Yu-zhen,LIN Hung-chou,LI Rong-jian,et al.Stability analysis of unsaturated soil slope under transient seepage flow state[J]. Rock and Soil Mechanics,2008,29(11): 2893－2897.

[5]吴梦喜,高蓮士. 饱和-非饱和土体非稳定渗流数值分析[J]. 水利学报,1999,30(12): 38－42.WU Meng-xi,GAO Lian-shi. Saturated unsaturated unsteady seepage numerical analysis[J]. Journal of Hydraulic Engineering,1999,30(12): 38－42.

[6]MEHL S. Use of Picard and Newton iteration for solving nonlinear ground water flow equations[J]. Ground Water,2006,44(4): 583－594.

[7]WILLIAMS G A,MILLER C T,KELLEY C T.Transformation approaches for simulating flow in variably saturated porous media[J]. Water Resources Research,2000,36(4): 923－934.

[8]MILLER C T,ABHISHEK C,FARTHING M W. A spatially and temporally adaptive solution of Richards’equation[J]. Advances in Water Resources,2006,29(4):525－545.

[9]TAN T S,PHOON K K,CHONG P C. Numerical study of finite element method based solutions for propagation of wetting fronts[J]. Journal of Geotechnical andGeoenvironmental Engineering,ASCE,2004,130(3):254－263.

[10]PHOON K K,TAN T S,CHONG P C. Numerical simulation of richards equation in partially saturated porous media: Under-relaxation and mass balance[J].Geotechnical and Geological Engineering,2007,25(5):525－541.

[11]CHENG Y G,PHOON K K,TAN T S. Unsaturated soil seepage analysis using a rational transformation method with under-relaxation[J]. International Journal of Geomechanics,ASCE,2008,8(3): 207－212.

[12]MUALEM Y. A new model for predicting the hydraulic conductivity of unsaturated porous media[J]. Water Resources Research,1976,12(3): 513－522.

[13]VAN GENUCHTEN M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America,1980,44(5):892－898.

[14]CHEN X,TOH K C,PHOON K K. A modified SSOR preconditioner for sparse symmetric indefinite linear systems of equations[J]. International Journal for Numerical Methods in Engineering,2006,65(6): 785－807.