地下洞室围岩脆性破坏时的应力特征研究
王成虎,宋成科,刘立鹏
(1. 中国地震局地壳应力研究所,北京 100085;2. 中国水利水电科学研究院 岩土工程研究所,北京 100048)
1 引 言
高地应力作用是岩体地下工程需要重点考虑的影响因素之一[1],笔者在文献[1]中对高地应力的研究现状及具体判定标准进行了详尽地讨论。然而清楚了高地应力的概念后,工程设计人员更为关注的是高地应力作用下隧道围岩的变形破坏表现形式。在高地应力作用下,隧道围岩的变形破坏分为两类,一类是严重的脆性破坏或者岩爆,另一类就是围岩大变形[2],如图1所示。

图1 高应力作用下在地下空间开挖周边常见的两种破坏方式及其与强度应力的关系(据文献[2],有修改)Fig.1 Two common failure phenomena around one underground opening under the actions of high stresses and their relationships with the strength-stress ratio (Reference [2],modified)
国内学者对众多岩爆工程实例进行了详尽的研究,如秦岭隧道[3]、二郎山公路隧道[4]、太平驿隧道[5]等。国内研究的重点包括地下开挖面周边最大切向应力与围岩岩石单轴抗压强度的比值、实测最大主应力与围岩岩样单轴抗压强度的比值、围岩的弹性能量指数、围岩脆性系数以及围岩的完整性系数等。研究的目的侧重于岩爆的预测和预防,对岩爆发生的岩石力学机制和特征研究相对较少。而根据Martin等[6]的研究可知,实际上岩爆是地下空间围岩脆性破坏的一种特殊形式,渐变式的脆性破坏在国内称之为片帮,能够积累弹性应变能并且发生弹射的脆性破坏称之为岩爆。如图1所示,脆性破坏均发生在围岩相对完整,且岩体内蓄存的应力相对于岩体强度偏高的环境中。因此,把众多岩爆、钻孔崩落和地下空间围岩片帮研究的实例进行对比分析研究,或许能从另外一个侧面发现一些新的关于脆性破坏的统一认识。
2 岩爆及脆性破坏的判别指标分析
自从 1738年世界上最早记录并报道岩爆发生在英国南史塔福煤田的莱比锡煤矿起,岩爆研究工作就一直未停止过。根据各种不同行业内的工程实践,国内外学者提出了很多岩爆判据和岩爆分级标准[7],而本文的主要目的是为研究岩爆和脆性破坏时的应力特征,因此,列出与岩爆有关的应力以及应力强度比方面的判据,如表1所列。
由表1可以看出,众多岩爆判据中均主要考虑两个指标,一个是围岩岩样单轴抗压强度,一个是地下空间围岩岩体内的应力。地下空间截面内最大切向应力实际上是最大主应力或者工程区地应力张量的一个函数,最大切向应力和最大主应力从本质上来看反映的是同一个指标。而最大切向应力能够反映地下空间在开挖后的二次应力场的分布情况,或者说能够反映地下空间开挖后截面范围内的应力集中情况,因此,其与岩石单轴抗压强度的比值更能真实反映岩石破坏时的临界应力状态。地下空间截面内的最大切向应力可用式(1)估算,当然也可以利用弹性岩石力学理论的柯西解进行计算。
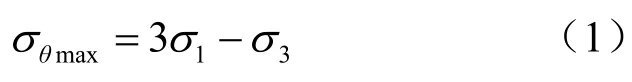
式中:σ1、σ3为工程场区原地应力张量中的最大、最小主应力。
由式(1)可知,地下空间截面内的最大切向应力一般会大于工程区的最大主应力,因而表1中各位学者所提出的发生岩爆的临界应力强度比十分接近。
Christiansson 和 Martin[8]在开展 ÄspÖ 硬岩地下实验室的岩芯钻探工作时发现,当工程场区的远场最大主应力与岩芯的单轴抗压强度之比在0.13~0.15时,在岩芯上开始出现微小的破坏,当达到0.28时,出现非常严重的破坏,在一些地段出现饼状岩芯现象,具体的破坏现象描述见表2列。
表2给出的实际观测结果与表1中陶振宇和姚宝魁给出的岩爆是否发生的临界值较为吻合,即当工程区远场应力最大主应力与单轴抗压强度的比值在0.15左右(即σ1/σci= 0.15±0.05)时,围岩岩体开始破坏,至于破坏的程度,取决于岩体质量、岩性等其他工程地质环境。
大量研究表明,钻孔崩落也是发生在地下开挖面周边的一种脆性破坏现象,迄今为止,Martin和其他的专家学者开展了大量的钻孔崩落的室内和现场试验,得到一些十分有价值的研究结论,根据Martin的总结,钻孔崩落现象出现时所需的钻孔截面内最大切向应力与岩石单轴抗压强度之比随钻孔孔径的增大而降低,当现场钻孔直径达到一特定值以后,发生钻孔崩落所需的起始应力强度比开始趋于一个稳定值,具体的数据如图2所示[9]。本质上,图2反映了随着钻孔直径增大,岩样或者现场围岩的整体强度在降低的趋势,进而反映在发生钻孔崩落的临界应力强度比的值逐渐降低。
Martin等[6]曾对大量的工程实例进行了分析研究,通过这些基于广泛岩体质量条件和岩性的工程实例的研究,得出当地下空间截面内最大切向边界应力与岩块实验室单轴抗压强度的比值超过0.4±0.1时,地下空间开挖面上会出现应力诱发的脆性破坏。
Harrison和 Hudson等[10]曾对几个国家的实测应力资料进行统计研究,发现实测原地应力的最大主应力、最小主应力和中间主应力两两之间的比值非常稳定,见表3。
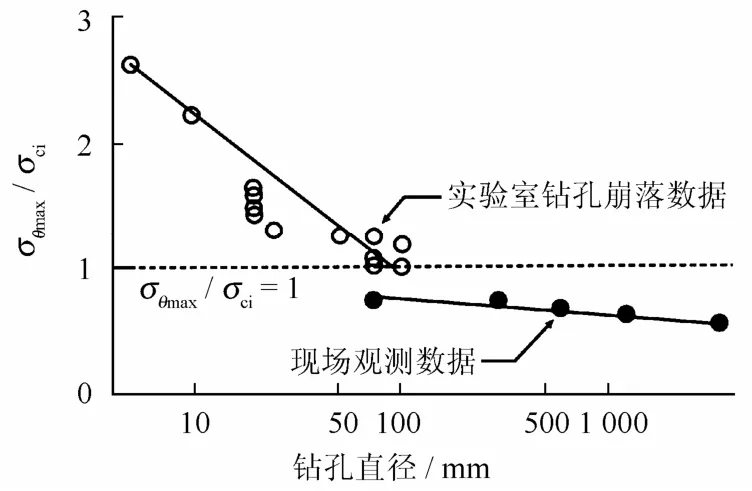
图2 不同孔径下发生钻孔崩落时的计算最大切向应力与岩石单轴抗压强度比值Fig.2 Ratio of the calculated tangential stress to σcat which breakouts initiate for various borehole diameters

表3 主应力比值汇总分析Table3 Summary of principal stress mean ratios
利用表 3给出的平均值再结合式(1)对陶振宇、姚宝魁和表2中的数据进行变换,即可得到陶振宇判据所对应的发生轻微岩爆或者脆性破坏的最大切向应力与岩石单轴抗压强度的比值为 0.179~0.468;而姚宝魁判据对应的应力强度比为 0.39~0.52;表 2中第 2行对应的应力强度比为 0.338~0.39。由此可见,表1中除了Russense方法给出的脆性破坏的初始应力强度比不在 σθmax/σci= 0.4±0.1所表示的范围内,其余表1和表2的内容均满足了σθmax/σci= 0.4±0.1的要求。
综合上述分析可知,本质上来说地下空间周边围岩中的岩爆和脆性破坏的发生具备相同的应力背景条件,发生脆性破坏、钻孔崩落和轻微岩爆所需的应力条件基本是相吻合的。如果用地下空间截面内的最大切向应力与实验室岩样单轴抗压强度之比来描述,那么该条件应该为 σθmax/σci= 0.4±0.1;如果用工程区范围内实测最大主应力与实验室岩样单轴抗压强度之比来描述,那么该条件应该为σ1/σci=0.15±0.05。
3 岩爆及脆性破坏的工程实例分析
前面利用大量的研究成果对岩爆或者脆性破坏发生时的应力环境条件进行了详细地分析论述,前人的研究成果都是基于特定的工程实例、室内和现场试验得到的一般性规律和经验准则,而这些结论对于其他工程的适用性如何仍然有待验证。下面结合国内外的岩爆和脆性破坏的工程实例对上述结论予以论证。
Martin[6]分析圆形和类圆形地下空间脆性破坏深度时总结了大量工程实例中脆性破坏深度与最大主应力的关系,如表4所列(表中*为圆形隧道)。表中,Rf为从圆形地下空间圆心到最大脆性破坏深度点的距离,a为圆形地下空间的半径,如图1所示。笔者为了更好地验证第1节所述的规律,也对表中的数据按照式(1)求得 σθmax,并分别求得σ1/σci、σθmax/σci的比值。统计发现,发生脆性破坏时,σ1/σci≥0.15,σθmax/σci≥0.40。

表4 国外工程中脆性破坏深度与实测最大主应力的关系(据文献[7],有修改)Table4 Summary of case histories used to establish relationship between depth of failure and maximum principal stress (Reference [7],modified)
张志强等[11]对国内外的隧道岩爆案例进行过统计分析,具体的工程案例如表5所示。据统计分析,在发生岩爆的隧道工程实例中,大多数案例的σ1/σci比值在0.15~0.4之间,占整体发生率的80.8%;而在 0.2~0.3之间出现的频率最高,占整体发生率的 46.2%。文献[11]指出,确定发生岩爆的最小临界值σ1/σci= 0.15是比较恰当的。为了更好地揭示脆性破坏或者岩爆的应力背景条件,笔者对文献[11]中的工程案例依据式(1)进行变换计算,并求得 σθmax/σci的值,计算发现,所有岩爆工程实例均满足前面所述的 σθmax/σci≥ 0.4±0.1 的应力条件。

表5 国内外隧道工程发生岩爆的统计(据文献[11],有修改)Table5 Summary of tunnel rock burst cases all over the world (Reference [11],modified )
综合表4和表5的结果,岩爆工程实例和脆性破坏的工程实例均揭示了极为相似的应力背景条件,而σ1/σci和σθmax/σci揭示的发生破坏时的临界应力条件实际是相同的,只不过前者只考虑了工程区远场最大主应力,而后者考虑了地下空间开挖后的应力的调整变化,即在地下空间开挖后围岩中的应力集中现象。
4 基于 Hoek-Brown准则的脆性破坏力学机制讨论
结合前人研究结论和工程实例的综合分析得到了发生脆性破坏时的应力条件的一般规律,而任何岩体中的破坏都应该满足岩体强度理论,而Hoek-Brown强度准则在分析硬岩破坏时具备十分明显的优势,同时Hoek-Brown强度准则在世界范围内得到了广泛的应用和认可,为了引述方便,下面简单介绍一下 2002版的 Hoek-Brown强度准则[12]。
在Hoek-Brown强度准则2002年的版本中,广义强度准则的形式没有发生改变,如式(2)所示,但与岩体质量有关的mb、s、α有了很大的变化,见式(2)~(6)。
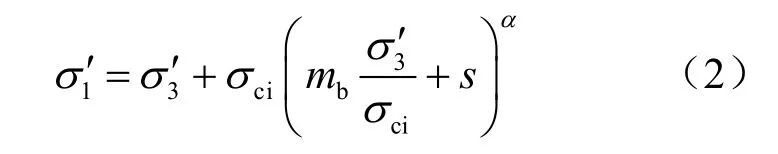
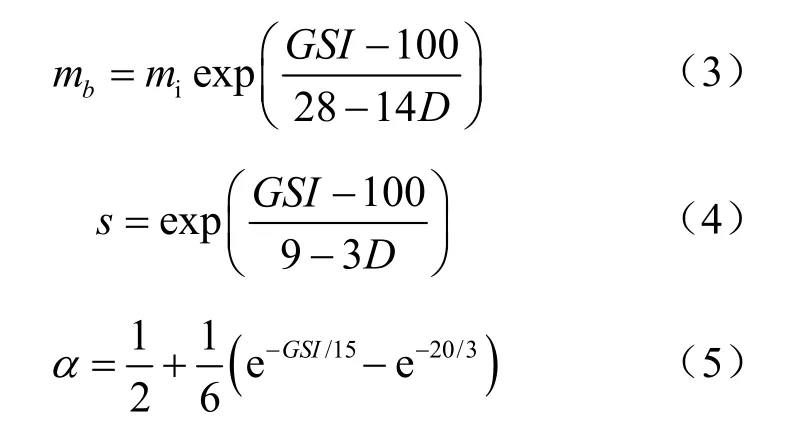
地下空间围岩的破坏一般是从开挖面的边界开始的,然后逐步向岩体内部延伸,在开挖面边界处,3σ′接近等于0,可以近似看作0,如果= 0,那么式(2)就变形为式(6)。将式(4)、(5)代入式(6),并作图,如图3所示。


图3 地下空间开挖面边界处破坏发生时应力条件与岩体分级的关系Fig.3 The relationship between GSI and the stress conditions when the failure initiates from the boundary of underground opening
由图3可知,在完整岩石发生破坏时,最大有效应力与岩石单轴抗压强度之比约为 0.3~0.5。在Hoek-Brown强度准则中,对于完整岩石,s = 1,根据式(6),最大有效主应力1σ′接近于σci时,岩体才开始破坏。然而,Read和Martin[13]在加拿大 AECL地下实验室完整花岗岩体中的现场开挖试验显示,即使GSI ≈ 100,估算的s也只有约0.25,那么≈0.5σci(在完整岩石中,取α = 0.5),而这一结果与南非地下采矿中取得的经验相类似,即s ≈ 0.20,岩石开始破坏时,≈ 0.4σci。Martin在文 献[6]中指出,这可能与现场岩体破坏和实验室单轴试验不同的加载路径有关,在实验室测试单轴抗压强度时是通过单向加载使得岩样发生破坏,而在地下空间开挖时是由于开挖卸载而导致地下空间围岩发生破坏。实际上,广泛开展的室内和现场钻孔崩落试验就有效回答了这个问题,如图2所示,在实验室内开展钻孔崩落试验,也是通过双向加载来实现的,而现场开展钻孔崩落等试验,则是通过开挖卸载实现的,仔细观察图 2,就会发现对于室内试验当钻孔孔径不断增大,σθmax/σci值越来越接近于 1,而现场试验的 σθmax/σci值则越来越接近于 0.5,这一规律也说明 Hoek-Brown准则在预测围岩脆性破坏时具备很高的准确性,同时在分析地下空间围岩脆性破坏时,不能简单地把设为0,因为围岩破坏是一个动态过程,在开挖过程中,围岩中的应力不断调整,围岩内部的裂纹也随之发展,进而岩体强度也不断劣化,随后在宏观上体现出围岩岩体的宏观破坏。
5 结 语
通过前面的论述可知,岩爆、钻孔崩落、片帮均可归于硬岩的脆性破坏现象,它们分别反映了高地应力作用下完整岩体不同的破坏程度,而在破坏时具备相同的应力背景条件。通过对前人广泛的研究成果和工程实例的综合分析可知,脆性破坏的应力条件可以用地下空间周边切向最大应力与岩石单轴抗压强度之比(σθmax/σci)或者工程区最大主应力与岩石单轴抗压强度之比(σ1/σci)来描述,两种指标本质上反映了相同的应力条件,对于σθmax/σci,σθmax/σci= 0.4±0.1是发生脆性破坏的应力临界条件;对于σ1/σci,σ1/σci= 0.15±0.05是发生脆性破坏的应力临界条件,这里两种指标都取了一个范围,主要是由于不同的岩体分级、岩性和工程地质条件会对指标的界定产生较为显著的影响。
近年来,岩体强度破坏已成为一个重要研究热点,而且岩体强度也把岩爆研究中的岩体完整性和单轴抗压强度统一到了一个指标,并且考虑了众多的岩体分级因素,因此,从岩体强度指标的角度来看待应力强度比对围岩脆性破坏的影响或许也会有新的发现,或许是下一步研究工作需要考虑的重点。
[1]王成虎,郭啟良,丁立丰,等. 工程区高地应力判据研究及实例分析[J]. 岩土力学,2009,30(8): 2359-2364.WANG Cheng-hu,GUO Qi-liang,DING Li-feng,et al.High in-situ stress criteria for engineering area and a case analysis[J]. Rock and Soil Mechanics,2009,30(8): 2359-2364.
[2]MARTIN C D,KAISER P K,CHRISTIANSSON R.Stress,instability and design of underground excavations[J]. International Journal of Rock Mechanics and Mining Sciences,2003,40: 1243-1256.
[3]谷明成,何发亮,陈成宗. 秦岭隧道岩爆的研究[J]. 岩石力学与工程学报,2002,21(9): 1324-1329.GU Ming-cheng,HE Fa-liang,CHEN Cheng-zong. Study of rockburst in Qingling tunnel[J]. Chinese Journal of Rock Mechanics and Engineering,2002,21(9): 1324-1329.
[4]徐林生,王兰生. 岩土二郎山公路隧道岩爆发生规律与岩爆预测研究[J]. 岩土工程学报,1999,21(5): 569-572.XU Lin-sheng,WANG Lan-sheng. Study of the laws of rockburst and its forecasting in the tunnel of Erlang Mountain road[J]. Chinese Journal of Geotechnical Engineering,1999,21(5): 569-572.
[5]周德培,洪开荣. 太平驿隧洞岩爆特征及防治措施[J].岩石力学与工程学报,1995,14(2): 171-178.ZHOU De-pei,HONG Kai-rong. The rockburst features of Taipingyi tunnel and the prevention methods[J].Chinese Journal of Rock Mechanics and Engineering,1995,14(2): 171-178.
[6]MARTIN C D,KAISER P K,MCCREATH D R.Hoek-Brown parameters for predicting the depth of brittle failure around tunnels[J]. Canadian Geotechnical Journal,1999,36(1): 136-151.
[7]张镜剑,傅冰骏,李仲奎,等. 应变型岩爆五因素综合判据及其分级[J]. 岩石力学与工程动态,2011,88(1):27-37.ZHANG Jing-jian,FU Bing-jun,LI Zhong-kui,et al.Criterion and classification for strain mode rockbursts based on five-factor comprehensive method[J]. News Journal of Rock Mechanics and Engineering,2011,88 (1): 27-37.
[8]CHRISTIANSSON R,MARTIN C D. Quantifying in-situ stress and its role in repository design[C]//The 6th North America Rock Mechanics Symposium (NARMS).Houston,Texas: American Rock Mechanics Association,2004.
[9]MARTIN C D,MARTINO J B,DZIK E J. Comparison of borehole breakouts from laboratory and field tests[C]//SPE/ISRM Rock Mechanics in Petroleum Engineering Conference. Delft,Netherlands: Society of Petroleum Engineers Inc.,1994.
[10]HARRISON J P,HUDSON J A,CARTER J N C. Is there a relation between the in-situ principal stress magnitudes in rock masses?[C]//Proceedings of 1st Canadian-US Rock Mechanics Symposium. Vancouver,Canada: Taylor& Franics,2007.
[11]张志强,关宝树,翁汉民. 岩爆发生条件的基本分析[J].铁道学报,1999,20(4): 82-85.ZHANG Zhi-qiang,GUAN Bao-shu,WENG Han-min.Basic analysis of rock bursting occurrence condition[J].Journal of the China Railway Society,1999,20(4): 82-85.
[12]HOEK E. Estimates of rock mass strength and deformation modulus[EB/OL]. http://www. rocscience.com /education /hoeks_corner.,2004-04-07.
[13]READ R S,MARTIN C D. Technical summary of AECL’s mine-by experiment,Phase 1: Excavation response[R]. Manitoba: Atomic Energy of Canada Limited,1996.

