岩爆、冲击地压的定义、机制、分类及其定量预测模型
钱七虎
(1. 解放军理工大学 国防工程学院,南京 210007;2. 解放军理工大学 爆炸冲击防灾减灾国家重点实验室,南京 210007)
1 引 言
随着交通和经济的发展,在深部地下空间修建了大量的矿井和隧道,矿井开挖深度已达地面下4 000 m,规划深度已达地下5 000 m,民用隧道最大埋深已超2 500 m。在修建大深度矿井和隧道时,岩爆已成为普遍问题[1],发生在南非、智利、加拿大、澳大利亚、俄罗斯等国的矿井以及挪威、美国、中国、瑞典、瑞士等国的隧道工程中。岩爆严重威胁着施工人员的安全,造成了巨大的经济损失。例如2010年11月28日发生于中国锦屏二级水电站2 500 m埋深的引水隧洞中的岩爆,导致了7人死亡和全断面岩石掘进机的严重损坏。
2 岩爆的机制和定义
虽然国内文献中关于岩爆的机制、定义和分类众说纷纭,不尽一致,但是国际上研究岩爆的权威学者关于岩爆的定义、机制和分类是基本相同的。
岩爆是一个物理现象,所以其定义应是现象的描述,以下引述了若干定义和机制:
(1)岩爆是突然的岩石破坏,其特征是岩石的破碎和从围岩中突出并伴随着能量的猛烈释放[2]。
(2)开挖一个新地下孔洞或者改变一个已有孔洞造成围岩中的应力变化,这些应力变化能导致孔洞附近岩体的破坏,或者诱发已有断裂的滑移[3];第1类岩爆定义为已有断裂的滑移,第2类岩爆定义为一定体积的岩石的脆性破坏[3]。
(3)为了发生断裂型岩爆,原生的或感生的应力水平必须足够高,以能激活原生的断层面的运动,或启动地质结构面的活动,或者在岩体中形成断裂(新断层),岩爆是岩体动力破坏的后果[1]。
(4)矿井中动力现象(岩爆)的本质是围岩获得了动能[4]。
(5)采矿诱发的岩爆是与平衡状态的失稳相连的,它可以包括:①已有断裂面的滑移;②岩体的破裂[3]。
3 岩爆的分类和冲击地压
岩爆因其表现形式的不同,形成不同类型的岩爆,但其物理现象的本质是相同的,所以都应称为岩爆。
“地震性事件”、“动力事件”、“动力现象”、“动力失稳”、“突变”、“突变形式的失稳”都是同义的,都意味由一个平衡状态向另一个状态的突变,伴随着剩余能量以应力波形式的释放。它可以发生于不同的尺度:在加载试件中,它呈现于微观尺度和颗粒形式,伴随着声发射;在矿井中,它不仅有声发射,而且有岩爆;在地壳中,除了相对小的突变外,有时还发生十分猛烈的突变,如地震[5]。
两类岩爆为两类突变,即体积性失稳和接触面失稳[5]:Ⅰ型岩爆,由断层滑移事件所导致的;Ⅱ型岩爆,由岩石破坏所导致的,它们包括围岩应变岩爆和岩柱应变岩爆[3]。
岩爆形式的动力破坏,基本可以区分为2类:第1类,通常称为应变型岩爆,是由岩石破坏导致的;第2类是断层滑移或者剪切断裂所导致的。两类岩爆的主要差别是:在第1类中,扰动源(开挖)和岩爆破坏部位是相重合的;在第2类中,其扰动源和所导致的岩爆破坏部位可以分离相当大的距离。与第2类滑移断裂型岩爆相联系的能量通常甚大于应变型岩爆的能量。断裂滑移型事件的岩爆破坏通常远比应变型岩爆事件强烈得多,在矿井环境中通常在单一事件中有数十米或者甚至数百米巷道被破坏[1]。
硬岩矿井中大量的地震性事件属于剪切型,或滑移型失稳类[6]。
累积的证据导致的结论是:在南非矿井中,剪切型,也可能是沿已有断裂面或新鲜断裂面滑移型破坏的矿震起了优势地位[7]。
切不可忽视爆炸波对触发煤爆的影响。门头沟矿在700~900 m深处的114起煤爆中,有89起(占78%)是因爆破触发的,在龙凤矿700 m深处因爆破而触发的煤爆也超过总数的50%。由此可以推断,在这样的深度,煤一定是处于准稳定平衡状态,爆炸波的触发作用能导致死亡事故发生。有些矿也出现过顶板爆裂,坚硬岩层顶板更为不利的影响是爆裂会扩展而远远超前于长壁工作面,从而导致失稳和煤爆[8]。
为了分析冲击地压和岩爆的异同,下面再介绍中国煤矿的两个实际冲击地压事故的调查结论。
(1)华丰煤矿冲击地压事故综合剖析:4层煤的多个工作面发生过冲击地压。华丰井田煤系地层以上为500~800 m砾岩层,砾岩层坚硬整体性强,其断裂跨落对下部的煤岩体产生冲击载荷,是4层煤工作面发生冲击地压的主要力源。
(2)义马煤业集团千秋煤矿“11·3”重大冲击地压事故调查报告:10人死亡、64人受伤,本矿区煤层顶板为巨厚砂砾岩(380~600 m),事故发生区域接近落差达50~500 m 的F16逆断层,地层局部直立或倒转,构造应力极大,处在强冲击地压危险区域;煤矿开采后,上覆砾岩层诱发下伏F16逆断层活化,瞬间诱发了井下能量巨大的冲击地压事故。
有了上述关于岩爆的定义、机制和分类的描述,特别是陈宗基关于煤爆的认识以及两个煤矿实际冲击地压事故的调查结论,可以得出如下关于冲击地压发生机制的判断:在多层多巷开挖的矿井中,巷道的围岩(煤)由于采矿的多次开挖所积累的大量破裂,使已连续破碎和不连续破碎块系处在准稳定平衡状态,这种准稳定平衡状态主要属于接触面准平衡,即剪切准平衡状态,当爆破时或顶板断裂时,爆炸波的传播与顶板断裂的冲击诱发了该准平衡块系的失稳,导致冲击地压的发生,这种冲击地压究其发生机制,是与断裂滑移型或剪切型岩爆为同一类型,也是广义岩爆的一类。
4 岩爆的定量预测和数值模拟
岩爆造成人员伤亡和设备损坏的后果使得岩爆的预测预报十分必要和紧迫,但是岩爆发生机制的复杂性使得岩爆的预测、预报十分困难。首先对岩爆发生时间的准确预报实际上是不可能的,这是由岩爆发生机制的随机性和复杂性所决定。但是岩爆的发生主要是由地下深部岩体的开挖所引起的地应力变化所决定,因此地质勘察技术、地应力检测技术、基于岩石力学理论和方法以及计算技术的岩石力学数值模拟技术的长足发展,使得岩爆发生处以及等级的定量预测和数值模拟成为可能。
岩爆研究的权威学者认为定量预测的时代已经到来,如此的定量进展需要通过数值模拟和现场观测的精细结合才可实现[1,4]。
4.1 应变型岩爆的定量预测原理
应变型岩爆再可分为两类,在矿井中常留有岩(煤)柱,岩柱的岩爆和巷道围岩的岩爆其定量预测原理稍有不同,分述如下。
4.1.1 岩(煤)柱应变型岩爆的定量预测[3]
岩柱应变型岩爆的预测是基于矿井中岩柱的动力破坏(岩爆)与岩石试件在柔性试验机上发生猛烈破坏的机制相似。众所周知,为了获得岩石试件单轴抗压全应力-应变曲线,需要在刚性试验机上进行,这是20世纪50~60年代Petukov[9-10]和Cook[11]所指出的,反之在柔性试验机上岩石试件在应力下降段上则发生猛烈破裂,所谓刚、柔是指试验机与试件刚度之比较,试验机刚度大于试件刚度,则为刚,反之则为柔。图1所示即为两者相对刚度的影响。
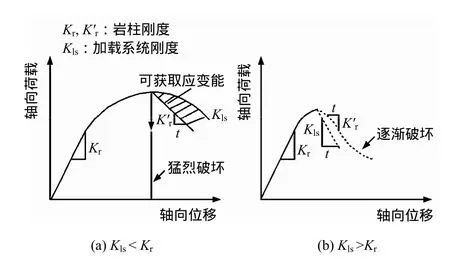
图1 单轴加载条件下加载体系和岩石试件相对刚度对破坏特性的影响[11]Fig.1 Impact of relative stiffness between rock specimen and loading system under uniaxial loading on destruction of property
岩柱岩爆定量预测的关键是如何计算岩柱和围岩的刚度,如果岩柱峰后刚度大于围岩刚度,则可能发生岩爆,否则,则发生渐变性破坏(塌方)。
(1)岩柱刚度( Kpr、 Kp′r)计算
①长岩柱(平面应变型)刚度(单位厚度):


式中:E、E′为峰值前、后岩体弹性模量;v为泊松比;B为柱宽;H为柱高。
②相应对于窄岩柱(柱厚为S),则有

(2)围岩刚度(Kls)计算
计算模型见图2。
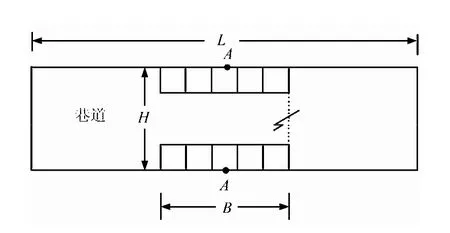
图2 围岩刚度计算模型Fig.2 Analytical model for stiffness of surrounding rocks
对长岩柱进行二维计算,对窄岩柱则由二维改为三维,数值计算点A的荷载 BSσp与位移D曲线;求其曲线斜率即为围岩的局部刚度岩爆(猛烈破坏);逐渐破坏(塌方)。
以上判别该岩柱是否发生岩爆的机制、岩柱岩爆等级的定量预测的原理,与下述围岩应变型岩爆的相同,此处不再赘述。
4.1.2 围岩应变型岩爆定量预测
为定量预测围岩应变型岩爆的位置、规模和岩块弹射速度,需要解决以下3个问题[12]:
(1)何处发生围岩破裂:基于非协调变形分析的非欧几何模型确定开挖卸荷后在洞室围岩中形成的应力场[12]。
(2)围岩破裂为何发生:为此需要确定围岩各点储存的应变能和破裂耗散能,后者的确定要研究岩石破裂的起裂准则和裂纹的扩展(包括稳定扩展和失稳扩展)准则[12]。
(3)发生何种类型岩爆:需研究破裂区潜在型岩爆、即时型岩爆、时滞型岩爆发生的判别准则。
为解决第1个问题,岩体含有原生微裂纹以及岩爆的前提是岩体的破裂,所以,此时岩体不应看作连续的,不再满足应变协调方程,需采用建立在非欧几何模型上的非协调变形岩体的力学理论来计算洞室围岩中的应力场分布。基于非欧模型的解与围岩中的微破裂现象以及应力脉动现象是相一致的,而连续介质力学模型的解与此是不相一致的。
岩石介质为非均匀地质体,岩体中存在着不同尺度的原生微裂纹,其分布函数是随机的,可由岩体细观结构试验来确定。为简单计,采用一阶近似,假定原生微裂纹均匀分布,其尺度采用统计平均值,密度用平均化法获得。
对第2个问题,可用断裂力学理论来解决。围岩的破裂过程包括原生裂纹沿界面和向岩体内部扩展、次生裂纹的稳定扩展和失稳扩展、以及微裂纹合并形成宏观裂隙最终导致岩体破裂。
为解决第3个问题,首先应了解应变型岩爆的孕育和发展过程,它可概括为:第1阶段,开挖卸荷导致围岩的破裂和碎化;第2阶段,在围岩中应力梯度作用下,围岩碎块的运动加速直至弹射,与此同时,围岩的应变能转化为动能。
围岩应变型岩爆分类判据的建立基于能量原理,即动力破坏(岩爆)的本质是剩余能量转化为动能[4-5,9],因此破碎岩块的动能应近似等于高地应力围岩存储的应变能与耗散于岩石破裂的破坏能之差,然后根据这个原理进行分类:潜在型岩爆、即时型岩爆和时滞型岩爆。
(1)潜在型岩爆的机制:周围围岩已经破裂但没有发生岩爆;原生微裂纹和次生微裂纹扩展消耗的总能量大于或等于岩体中存储的弹性应变能(不存在剩余能量)。
(2)即时型岩爆的机制:次生微裂纹的长度大于临界值,于是发生失稳扩展形成宏观裂隙,所产生的的破裂区和洞壁相交,且次生裂纹扩展消耗的总能量小于围岩体存储的弹性应变能。
(3)时滞型岩爆的机制:围岩内所发生的破裂区与洞壁不相交;次生裂纹扩展消耗的总能量小于围岩体存储的弹性应变能,剩余能量转化为碎块动能;裂区岩块的运动足以导致至洞壁的最短路径上的围岩破裂并飞出。
4.2 断裂滑移型岩爆预测[5]
该岩爆预测基于下列考虑和假设:断裂面为单一的;这类岩爆是与作用在该断裂面上的剪抗力突变相联的;已有断裂和新断裂的区别在于前者的方向和位置独立于应力场的计算,而后者是由应力场计算决定的;断裂面合理地假设为平面,于是简化了计算,岩体是弹性的。
定量预测时首先要进行围岩开挖和爆破(动力作用)引起的应力场计算,即确定垂直于断裂面的正应力σ和断裂面上剪应力τ,然后对断裂面依照滑移发生判别准则进行判别:
相应的摩擦抗力τr为

对开挖卸荷诱发的,则有

对动力作用诱发的,则有

式中:σ为断裂面上的正压应力;μs为静摩擦系数;μ超为超低摩擦系数;c为黏结力。
若τ-τr>0,发生滑移,否则断裂面稳定不发生滑移(图3)。

图3 岩体断裂滑移示意图Fig.3 Slip failures of rocks
为预测岩爆的量级,需进行滑移后岩爆动能的计算:

式中:Wr为释放能;Wh为消耗于摩擦产生的热能;Wk为转化为动能的剩余能量。
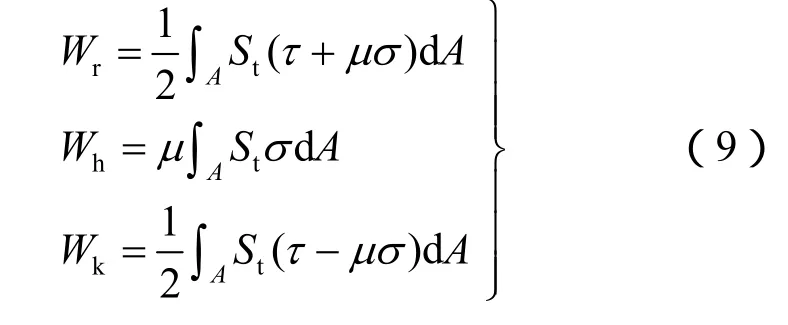
式中:St为滑移位移量;A为断裂面面积;μ为断裂面动摩擦系数;若为爆破诱发岩爆,则应为μ超。
进一步简化计算,τ、σ在滑移断裂面空间上假设为常量;断裂面为圆盘;滑移量取平均值SAV,则有

滑移时的剪应力降Δτ为

滑移量分布函数为
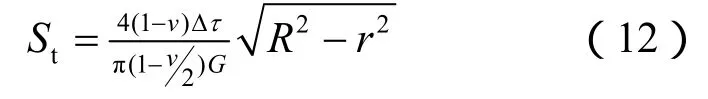
平均滑移量为

式中:R为断裂面的半径;r为滑移计算点的坐标;v泊松比;G为剪切模量。
4.3 岩石工程岩爆定量预测的流程[3]
具备以上所述的各类岩爆定量预测的原理和方法以后,可以着手进行实际岩石工程的定量预测,其预测的流程见图4。

图4 岩石工程岩爆定量预测流程Fig.4 Flowchart of quantitative forecasting for rockburst in rock engineering
在该流程中,步骤1是基础,只有掌握了该工程区域的地质结构面、初始地应力、岩体力学参数等情况和数据才能实施以下各步骤。步骤2是定量预测的关键步骤,只有分析了工程区域各分区的岩爆易感性,才能判定各分区岩爆发生的风险大小,区分轻重缓急进行岩爆的定量预测。步骤3应根据各工程分区有无地质结构面而定,有的需进行两种类型岩爆校核计算,有的仅需进行一种类型岩爆校核计算。步骤4按4.1和4.2所述内容进行。
4.4 岩体结构易爆易感性判定[3]
下面介绍3类岩爆易感的岩体结构,其他的情况应根据岩体开挖时的应力场计算和地质结构面具体部位来确定其岩爆易感性。
(1)图5(a)所示为巷道接近已有断裂进行开挖。开挖引起的应力变化将增加断裂的切应力,而减少断裂的法向压应力,两个变化都能诱发断裂滑移,故有可能导致断裂滑移型岩爆。
(2)图5(b)为当巷道开挖通过地质断裂面或岩性分区面的情况,此时若接近时未发生断裂滑移型岩爆,但临近断裂面的某区部分岩体进入破裂状态,取决于两区岩石的相对变形性质,该破坏也可能为猛烈破坏(岩爆)。
(3)图 5(c)为巷道沿断裂面或岩性分区边界开挖,则C区岩石为一岩柱,取决于A区、B区岩石与C区的变形性质,满足一定要求,C区岩石(岩柱)也可能为猛烈破坏(岩爆),该类情况也包括孤立的岩体结构的情况,即其呈现与周围岩体岩性不同或呈现几何的不规则性。
5 结 论
(1)从现象学出发对岩爆定义为,矿井或隧道的围岩或岩柱破坏、碎化发生崩出或弹射的现象,伴随能量的猛烈释放。岩爆发生的机制为,因开挖卸荷或动力作用诱发围岩中应力场的变化,或直接导致围岩的破坏碎化和弹射,或通过围岩中的已有断层和结构面滑移(活化)或新结构面滑移引起围岩破坏和弹射。

图5 岩爆易感的岩体结构Fig.5 Susceptive rock mass structures for rockburst
(2)岩爆的分类:第1类岩爆为应变型岩爆,或称体积不稳定(岩体破坏)导致的岩爆,其特点是扰动源和岩爆发生地一致;第2类岩爆为滑移型及剪切型岩爆,或称接触不稳定、通过断层或断裂面滑移导致的岩爆,其特点是扰动源(爆破或顶板断裂)和岩爆(冲击地压)发生地相距一定距离,第2类岩爆较第1类更普遍、更强烈,其破坏范围甚至达数十和几百米巷道。
(3)矿井中的冲击地压大部分属于第 2类岩爆,特别是多层多巷矿井中,围岩经过多次开挖卸荷,围岩已成为处于准稳定状态的新老结构面和破裂面所分割的岩块系,在动力作用(爆破或顶板断裂)下,岩块系失稳所导致。在矿井中,这类岩爆习称为冲击地压。
(4)对工程所在部位进行分区并判明各分区的岩爆易感性,分区的基础主要是地质勘察、地质结构面的判定、初始地应力值以及岩体力学参数的确定。有了分区的认识以及相关参数后,就可进行岩爆稳定性分析,稳定性分析的第1步是计算开挖或爆破作用产生的应力场,对于断裂滑移型岩爆,接下来是依据判别准则进行结构面(断裂面)稳定性校核和岩爆动能的估算;对于应变型岩爆,接下来是定性预测和按照断裂力学公式进行定量预测。
[1]STACEY T R. Dynamic rock failure and its containment[C]//Proceedings of the First International Conference on Rock Dynamics and Applications.Lausanne: CRC Press, 2013: 57-70.
[2]BLAKE W. Rockburst Mechanics[D]. Golden: Colorado School of Mines, 1967, 1: 1-64.
[3]DENIS E GILL, MICHEL AUBERTIN, RICHARD SIMON. A practical engineering approach to the evaluation of rockburst potential[C]//Rockburst and Seismicity in Mines. Rotterdam: A.A. Balkema, 1993: 63-68.
[4]LINKOV A V. Dynamic phenomena in mines and the problem of stability[D]. [S. l.]: University of Minnesota,1992.
[5]ALEXSANDER M LINKOV. Keynote lecture: New geomechanical approaches to develop quantitative seismicity[C]//Rockburst and Seismicity in Mines.Rotterdam: A. A. Balkema, 1997: 151-166.
[6]SALAMON M D G. Keynote address: Some applications of geomechanical modelling in rockburst and related research[C]//Rockburst and Seismicity in Mines.Rotterdam: A. A. Balkema, 1993: 297-309.
[7]RYDER J A. Excess shear stress in the assessment of geologically hazardous situations[J]. Journal of South African Institute of Mining and Metallurgy, 1988, 88:27-39.
[8]陈宗基. 岩爆的工程实录、理论与控制[J]. 岩石力学与工程学报, 1987, 6(1): 1-18.TAN TJONG-KIE. Rockbursts, case records, theory and control[J]. Chinese Journal Rock Mechanics and Engineering, 1987, 6(1): 1-18.
[9]PETUKOV I M. Rockbursts in Kizel coalfield mines[M].Perm: Perm Publ., 1979.
[10]PETUKOV I M, LINKOV A M. The theory of post-failure deformations and the problem of stability in rock mechanics[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1979, 16(5): 57-76.
[11]COOK N G W. A note on rockburst considered as a problem of stability[J]. Journal of South African Institute of Mining and Metallurgy, 1965, 65: 437-445.
[12]ZHOU X P, QIAN Q H. The non-Euclidean model of failure of the deep rock masses under the deformation incompatibility condition[J]. Journal of Mining Science,2013, 49(3): 368-375.

