基于边坡渐进破坏特征对传统极限平衡法几点假设的合理分析

曾 锃，张泽辉，杨宏丽，尹小涛，党发宁

(1. 西安理工大学 岩土工程研究所，西安 710048；2.浙江省水利水电勘测设计院，杭州 310002；3.西安长庆科技工程有限责任公司 建筑工程设计部，西安 710018；4.中国科学院武汉岩土力学研究所，武汉 430071)

1 前 言

边坡失稳破坏是一类常见的岩土工程问题，其失稳破坏不是一个突然、瞬间发生的整体破坏，而是一个局部破坏发展直至贯通的渐进破坏过程。

Skempton[1]最早研究了边坡失稳破坏问题。对于该问题的研究一般有极限平衡法和强度折减法两类，其中极限平衡法应用比较广泛。无论何种方法,主要提供滑动面位置和安全系数两种结果用于稳定性评价，计算的过程做了很多假设，即假设滑体为刚体；假设同时达到极限状态；针对的是一个虚拟的参数持续折减情况。对于破坏的标准，还没有一个统一的认识。有限元强度折减能部分反映变形过程，但受制于其理论的局限性，不能模拟破裂过程，而且，持续破坏的反应依靠强度的持续折减实现，这与材料破坏的局部化相悖。边坡的破坏也是一个多米洛骨牌式链式反应，而不是一直弱化。破坏面的形成也是一个点、线、面逐步扩展的过程，具有极强的时间序列效应。

对于边坡渐进破坏的研究，目前国内外基本有3类：（1）采用离心场非接触位移测量[2]或者 CT技术[3]测量出边坡的位移场，然后，通过数值模拟和反演分析等途径算出边坡的应力场，间接揭示边坡的破坏过程与应变局部化和应力集中的关系。（2）以局部化问题为切入点，采用基于弹塑性大变形原理，或者节理单元的有限元法，捕捉边坡中的剪切带的位置及其扩展情况，并根据局部化剪切带的扩展情况研究边坡的渐进破坏[4－10]。（3）以离散元，或者有限元与离散元的杂交元，模拟岩土材料的破坏问题，离散元的动力方程可以很好地揭示边坡的渐进破坏，问题的求解本身就是一个时间序列问题[11]。

本文利用颗粒流平台，设计了0.1 m粒径土质边坡模型，通过对其细观黏聚力折半来实现坡体的破坏，以考察这个强度参数对坡体渐进破坏过程和最终破坏形态的影响，探讨土质边坡渐进破坏过程。通过渐进破坏特征，探讨当前边坡计算中一些假设的合理性，也借此尝试一种研究边坡渐进破坏过程宏观、细观规律的方法。

2 计算模型及方案设计

2.1 计算模型

为使研究建立在同一物理背景下，方便对比分析，模型颗粒统一为0.1 m，宽30 m，高20 m。在x = -5.0 m处建立一条监测线，监测深度坡面至y =-6.0 m。测量球的半径为0.4 m，监测变量为x、xy方向应力。数值模型的颗粒间接触本构关系为黏结模型，重度为18.50 kN/m3，弹性模量为15.5 MPa，摩擦系数为0.36，黏聚力36.0 kPa。利用设置的1.0 m间距30条竖向颗粒组group来监测边坡滑动面的发展过程，如图1所示。

图1 颗粒流模型及监测点位置示意图(单位：m)Fig.1 Particle flow code model and monitoring positions(unit: m)

2.2 计算方案设计

在初始模型和初始参数下，施加体力后经试算模型不会发生破坏。为了能观察到边坡的渐进破坏过程，设计了只对初始模型颗粒间细观黏聚力折减一半(18 kPa)，目的是分析这个强度参数分别对破坏过程造成的影响。每20000个时间步保存一次边坡破坏形态，共计200000个时间步，10个边滑动面形态。

3 土质边坡渐进破坏过程分析

3.1 渐进破坏过程分析

首先分析细观黏聚力变化边坡渐进破坏过程和最终破坏形态的影响，每20000个时间步边坡滑动面形态整理成图 2。从图 2(a)看不出坡体变化，图2(b)局部已经有裂缝，图2(c)上部局部滑动面已经贯通，图 2(d)～2(f)上部滑体下滑，图 2(g)～2(j)上部滑体下滑，造成坡脚阻滑部位的次生剪切破坏，最终形成近似于弧形的滑动面。伴随着滑体的下滑，滑体逐步破碎。在初始滑动阶段，滑体可以近似为刚体，说明局部分析刚体极限平衡分析法有其合理性，但整体分析则是不合理的，而且。滑动面也是一个演化的过程。破坏过程中不涉及材料参数的人为改变或劣化，渐进破坏过程符合实际情况。

3.2 破坏过程中应力监测结果分析

本文分析图 2(c)和2(d)边坡开始破坏时内部应力的变化情况，x、xy方向应力监测结果（step 6000～8000）整理如图3所示。

从图 3(a)可见，剪应力随着时间的增加均有个先增再减的过程，其中5.6 m深度位置，在上下点均减小的区段有个增加的过程，该点附近为滑动面的位置。由图3(b)可见，剪应力随着深度的增加波动幅度逐步增加，整落规律和间隔基本类似。由图3(c)可见，x方向应力5.6 m以上监测点基本为正，5.6 m以下基本为负，说明坡体物质的运动方向相反，这说明滑面以上坡体物质往外运动。滑床以下，由于挤压作用反而往坡内运动，自然在该面附近形成滑动面。由图 3(d)可见，随着深度的增加，x方向应力逐步减小，反方向增加，与剪应力涨落规律正好相反。滑面应该在5.6～7.6 m高度位置。这些均说明，坡体应力的变化不是单调的，这与实际应力监测规律类似，区别于有限元计算结果。

图3 边坡开始破坏时应力变化情况Fig.3 Stress variation when slope began damage

4 与传统极限平衡法的对比

4.1 宏观与细观的关系

由于颗粒流方法是基于颗粒间细观参数进行的计算，区别于极限平衡法分析的宏观参数，两者之间存在一定对应关系。为使分析建立在同一物理背景下，对相同模型和尺寸的颗粒流模型先进行0、20、50 kPa三个围压下的压缩试验，以获取宏观参数，压缩实验试件尺寸(与边坡模型相同)，见图4(a)。图4(b)、4(c)分别为压缩曲线和摩尔圆。

图4 宏观参数与细观参数的关系Fig.4 Relationships between macro and meso parameter

模型输入参数见章节2.1。压缩实验曲线，限于篇幅，只给出单轴压缩的情况（见图4(b)），所得峰值强度分别为57.5、101.9、178.0 kPa，根据其及对应的围压所得3个摩尔圆（见图4(c)），即可建立宏观与细观的关系。

4.2 与极限平衡法的对比

根据摩尔圆获取的宏观强度参数黏聚力为 18 kPa，内摩擦角为24º，重度维持18.50 kN/m3。将其代入同比例geo-slope模型，所得安全系数和潜在滑动面果如图5所示。由图可见，两者对于均质坡还是比较接近的，后缘前缘的位置很接近，区别在于离散元的破坏面没有滑动面光滑，笔者认为，离散元的更接近于实际情况，因为有限块体或者有限元，不能反映动势能转换造成的坡体二次破坏和破坏面的二次地形改造作用。

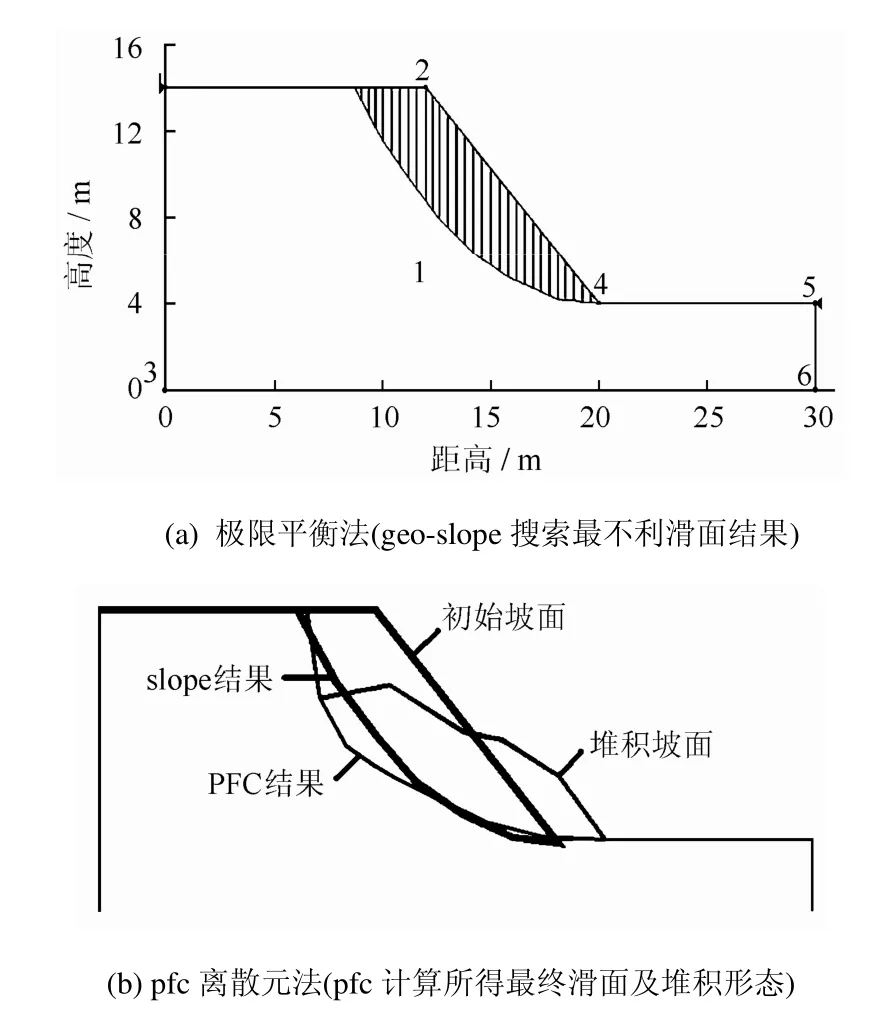
图5 破坏面与滑动面对比图Fig.5 Comparison between failure surface and sliding surface

5 结 论

（1）实际边坡的破坏是个渐进过程，先由局部开始，最终的弧形滑动面，是渐次形成的。

（2）开始边坡的破坏接近于刚体假设，随后坡体逐步破碎，次一级破坏面由于坡体物质的继续运动逐步形成，刚体假设失效，整体分析存在问题。

（3）坡体内应力的变化不是单调的，有涨有落。滑面附近应力不是同时达到极限状态。滑面和坡体物质堆积形态是滑坡的最终表现，不能作为整体分析的依据。

离散元的动力方程能很好地反映边坡破坏的时间效应和渐进破坏特征，也能很好地模拟岩土材料的破坏特性，是未来该领域研究的前沿性方向。

[1]SKEMPTON A W. Long term stability of clay slopes[J].Geotechnique,1964,14(1): 77－101.

[2]张嘎,王爱霞,牟太平,等. 边坡破坏过程离心模型试验的应力位移场研究[J]. 岩土力学,2008,29(10): 2637－2641.ZHANG Ga,WANG Ai-xia,MU Tai-ping,et al. Study of stress and displacement fields in centrifuge modeling of slope progressive failure[J]. Rock and Soil Mechanics,2008,29(10): 2637－2641.

[3]OTANI J,KIKUCHI Y,MUKUNOKI T. Investigation of progressive failure in composite soils using an X-ray CT scanner[J]. Geomechanics,ASCE 2003,172(37): 642－653.

[4]杨令强,马静,陈祖坪. 岩质边坡渐进破坏的三维随机分析[J]. 岩土力学,2009,30(2): 468－473.YANG Ling-qiang,MA Jing,CHEN Zu-ping.Three-dimensional stochastic analysis of progressive failure of rock slopes[J]. Rock and Soil Mechanics,2009,30(2): 468－473.

[5]王志伟,王庚荪. 裂隙性黏土边坡渐进性破坏的FLAC模拟[J]. 岩土力学,2005,26(10): 1637－1640.WANG Zhi-wei,WANG Geng-sun. FLAC simulation for progressive failure of fissured clay slope[J]. Rock and Soil Mechanics,2005,26(10): 1637－1640.

[6]刘开富,谢新宇,张继发,等. 土质边坡的弹塑性应变局部化分析[J]. 岩土工程学报,2008,30(增刊): 291－294.LIU Kai-fu,XIE Xin-yu,ZHANG Ji-fa,et al.Elastoplastic strain localization analysis of soil slope[J].Chinese Journal of Geotechnical Engineering,2008,30(Supp.): 291－294.

[7]CHOWDHURY R N,TANG WH,SIDI I. Reliability model of progressive slope failure[J]. Geotechnique,1987,37(4): 467－481.

[8]CHOWDHURY R N. Probability model of progressive failure of slopes[J]. Journal of the Geotechnical Engineering Division,American Society of Civil Engineering,1982,108(6): 803－819.

[9]EBERHARDT E,STEAD D,COGGAn J S. Numerical analysis of initiation and progressive failure in natural rock slopes-the 1991 Randa rockslide[J]. International Journal of Rock Mechanics & Mining Sciences,2004,41: 69-87.

[10]GENCER M. Progressive failure in stratified and jointed rock mass[J]. Rock Mechanics and Rock Engineering,1985,18: 267－292.

[11]SCHOLTES L,DONZE F V. Modelling progressive failure in fractured rock masses using a 3D discrete element method[J]. International Journal of Rock Mechanics & Mining Sciences,2012,52: 18－30.