绞合式光纤的微弯损耗机制及其应用研究

茶国智

（大理学院工程学院，云南大理 671003）

绞合式光纤的微弯损耗机制及其应用研究

茶国智

（大理学院工程学院，云南大理 671003）

深入研究绞合式光纤的微弯损耗机制，提出两种微弯损耗模型且给出了相应的理论表达式，经理论分析和数值模拟表明两种模型都具有一定的合理性。同时，还对绞合式光纤的传感检测应用做了一些探讨。

绞合式光纤；微弯损耗机制；微弯损耗应用

利用光纤的微弯损耗可以实现传感检测，在医疗、交通、电力、机械、航空航天等各个领域都有广泛的应用前景。据此，下面拟对一种特殊的梯度型光纤微弯损耗——绞合式光纤微弯损耗进行研究。

1 微弯结构和损耗机制

1.1 微弯结构 将两光纤间进行绞合，其形状如图1。绞合处就会形成光纤的微弯曲，在此微弯曲处将产生微弯损耗。

图1 光纤绞合形状

任一光纤微弯曲的几何形状实际上为圆柱螺旋线形，图中r、R分别表示纤芯半径和光纤半径，h表示绞合螺距。在下面的处理中将一个螺距的绞合光纤段称为一个微弯段（简称微弯）。整个绞合段由这样的若干个微弯构成。

1.2 损耗机制

1.2.1 余弦曲率脉冲模型

1.2.1.1 微弯的曲率脉冲模型——余弦型 设理想光纤轴与坐标系z轴重合，则此时光纤轴的第n个微弯（段）可由螺旋线方程表示为：x=Rcos θ，y=Rsin θ，z=hθ/2π，其中θ表示螺旋线升角且取2nπ≤θ＜2（n+1）π，R、h的含义同前述。则此时光纤轴的第n个随机微弯可用横向（即x和y向）上偏离z轴的距离（fz）和g（z）来描述：

绞合段内N个微弯曲率函数称为一系列曲率脉冲，并可根据曲率函数公式推导出这些曲率脉冲，可表示为：

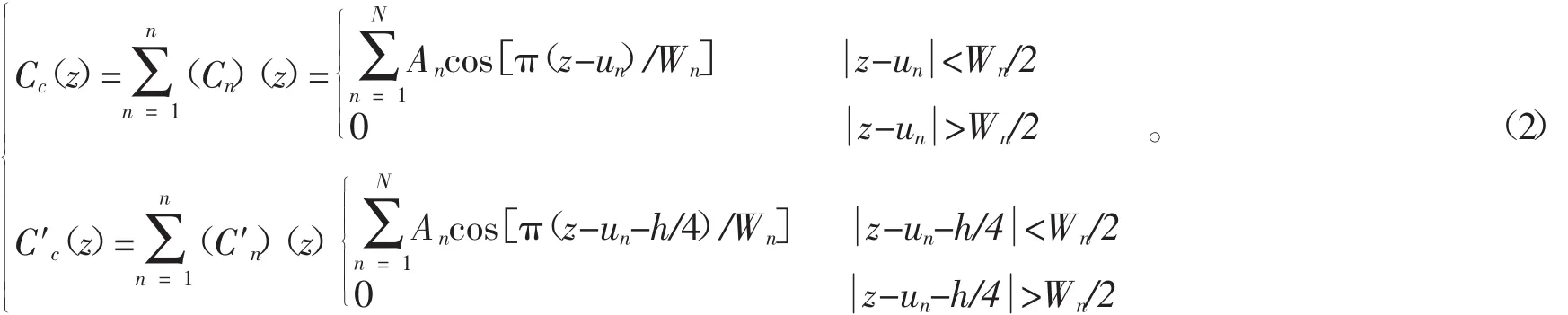
可见这些微弯的曲率脉冲为余弦型。在（2）式中下角标字母C表示余弦型，C（nz）和C′（nz）表示第n个微弯在x和y向的曲率函数，An为其曲率脉冲峰值，Wn为其曲率脉冲宽度。

1.2.1.2 功率谱密度 根据功率谱密度的定义〔1-2〕，可求得曲率函数的功率谱密度，故与（2）式相应的功率谱密度为：

1.2.1.3 微弯损耗 文献〔1〕给出了梯度多模光纤微弯发生在一个平面（二维）内时的损耗公式，而未给出发生三维微弯时的损耗式。但是可经过一系列繁琐的推导，得到适用于圆柱螺旋形微弯的损耗式：

将式（3）代入（4）式得：

可见，当△、r、R一定时，损耗取决于N、h。

注：该模型作者已在文献〔3〕中提出，此处稍作形式上的变换。下面提出另外一种新的模型。

1.2.2 矩形曲率脉冲模型

1.2.2.1 微弯的曲率脉冲模型——矩形型 圆柱螺旋线具有一个重要特性：其各点曲率都相同。如前所述绞合光纤微弯曲的几何形状为圆柱螺旋线形，则根据螺旋线方程可推知微弯处各点曲率都为：A=4π2R［/h2+（2πR）2］。根据这一特点，可假想将每个三维的圆柱螺旋线微弯段展开为一段二维的圆弧（因圆弧各点的曲率也相同），即三维变为二维。由于实际绞合光纤形成的圆柱螺旋线的饶率较小，因此这种设想是合理的。

微弯视为二维圆弧后，绞合段内N个微弯曲率函数（亦可称为曲率脉冲）可表示为

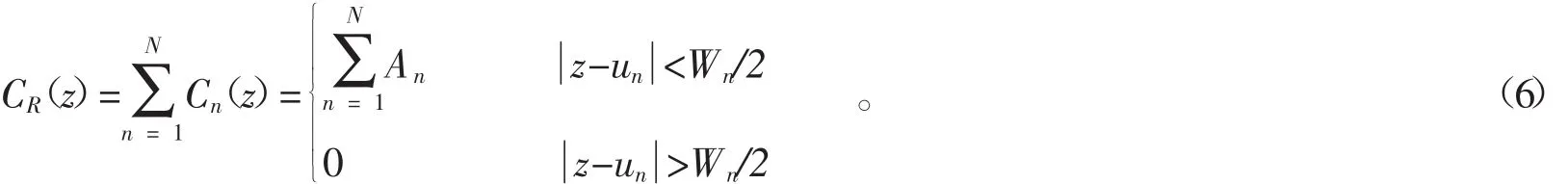
可见这些微弯的曲率脉冲为矩形型。在（4）式中下角标字母R表示矩形型，C（nz）表示第n个微弯的曲率函数，un为第n个随机微弯在z轴上的位置。An为其曲率脉冲峰值，Wn为其曲率脉冲宽度。

1.2.2.2 功率谱密度 由（4）式可求得其功率谱密度ζ（″△β）

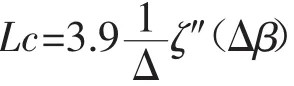
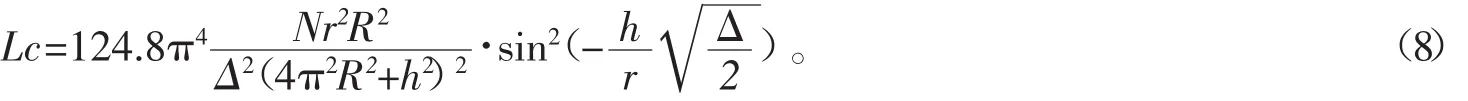
同样可见，当△、r、R一定时，损耗取决于N、h。

2 数值模拟与分析比较

2.1 数值模拟 假设选用的多模石英梯度光纤其参数为：2r/2R=62.5/125 μm、△=0.01，对（5）式和（8）式进行数值模拟，可分别得图2和图3。

1）余弦曲率脉冲模型

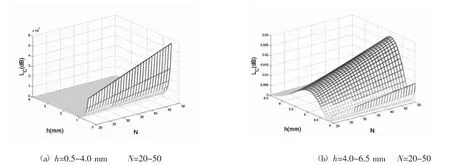
图2 微弯损耗Lc与h、N间关系

2）矩形曲率脉冲模型

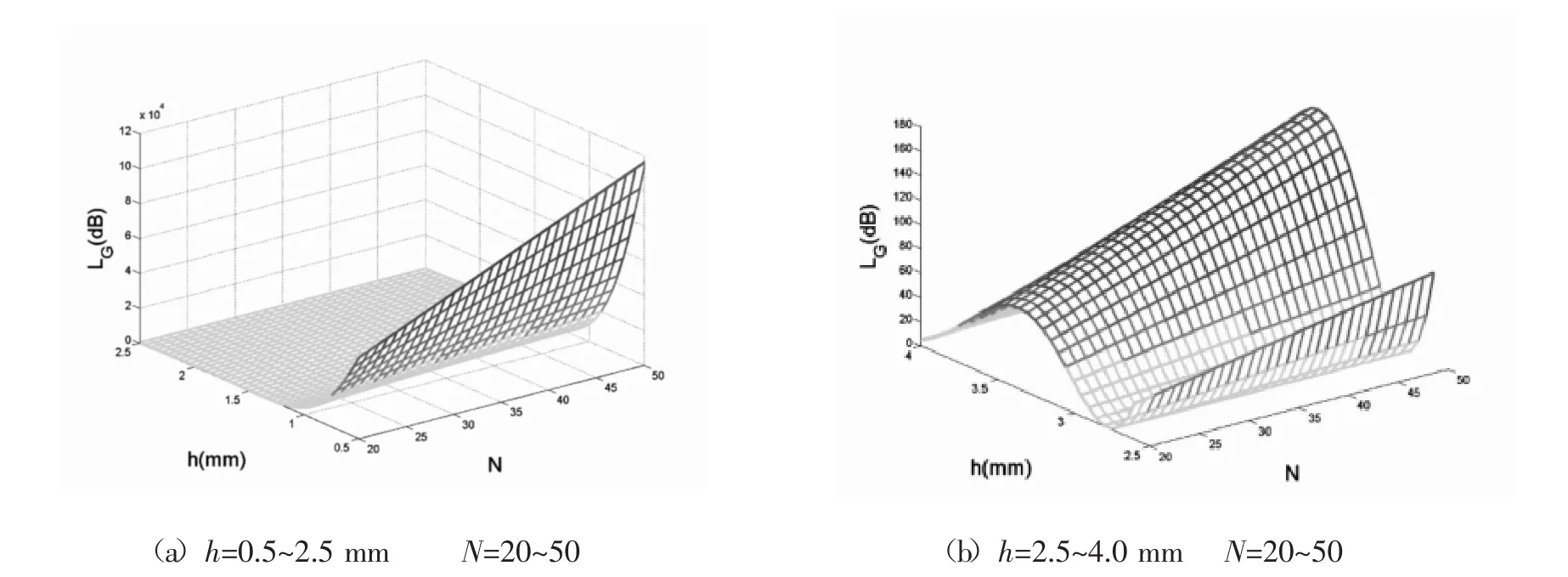
图3 微弯损耗Lc与h、N间关系

2.2 分析比较

第一，比较（5）式和（8）式可见，两模型的表达式相似：绞合式光纤的微弯损耗都由三角函数部分和除三角函数部分外的部分之积构成。三角函数部分为调制部分，除三角函数部分外的部分为幅值部分。故微弯损耗按幅值受调制的趋势变化。这也在图2和图3中可见。

第二，两模型反映的数值关系也基本一致：当△、r、R一定时（亦即选定光纤），绞合式光纤的微弯损耗受螺距h调制，而与微弯数N成正比。见图2、图3。

第三，两模型的幅值大小不同，实际应用中反映为初始损耗不同。这可通过比较图2中Lc和图3中Lc的可见。

第四，两模型的调制部分所决定的极值位置不同。这可通过比较图2（b）中h=2.5～4.0 mm和图3（b）中h= 4.0～6.5 mm可见。

总之，两种模型得到的微弯损耗均按幅值受调制的趋势变化，这正是光纤微弯损耗已被实验所验证的特点〔4〕，故两种模型都是合理的。只是两模型初始损耗大小和调制极值位置不同而已，这些需要实验进一步验证之，看哪个更合理？但遗憾的是目前没有很好的测试条件去完成。

3 应用研究

传感检测思想：只要将待传感检测参数的变化转化为螺距h变化，进而转化为光纤微弯损耗的变化即可。目前文献〔5-6〕来看，已有对应变参数的传感检测，即将应变参数的变化转化为螺距h变化，最终通过检测光纤的微弯损耗的变化实现对应变的传感检测。

基于上述的思想，可寻求更广阔的应用领域。

4 结束语

本文对绞合式光纤的微弯损耗机制提出了两种模型，即余弦曲率脉冲模型和矩形曲率脉冲模型，且给出了相应的理论表达式，并通过数值模拟以及理论分析比较等手段论证了两种模型的合理性。同时，还对绞合式光纤的微弯损耗的传感检测应用方面做了探讨。

〔1〕叶培大.光纤理论〔M〕.上海：知识出版社，1985：78-119.

〔2〕叶培大，吴彝尊.光波导技术基本理论〔M〕.北京：人民邮电出版社，1981：315.

〔3〕茶国智，姜向东，王少敏.一种监测管道形变的于光纤自缠绕式微弯传感器〔J〕.计量技术，2002，15（1）：34-37.

〔4〕Lagakos N.Microbend fiberoptic senso〔rJ〕.Applied Optics,1987,26(11):2171-2180.

〔5〕杨建良，郭照华，查开德.绞合式光纤应变传感器〔J〕.力学学报，2001，33（2）：284-287.

〔6〕杜彦良，金秀梅，孙宝臣，等.基于普通光纤的螺旋缠绕式准分布光纤传感器研究〔J〕.工程力学，2004，21（1）：48-51.

Research on Microbend Losses Mechanism and Application ofTwisted OpticalFiber

CHA Guozhi

（College of Engineering，Dali University,Dali,Yunnan 671003,China）

Via research on microbend losses mechanism of twisted optical fiber,this paper presents two novel theories of microbend losses and their respective formula,whose rationality is proved by virtue of theory analysis and numerical simulate.In addition,the application potential of twisted optical fiber is deliberated.

twisted optical fiber;microbend losses mechanism;microbend losses application

TP212.14［文献标志码］A［文章编号］1672-2345（2012）04-0035-04

大理学院科研基金项目（2007X43）

2011-06-27

茶国智，副教授，主要从事光电检测与信息处理技术研究.

（责任编辑 袁 霞）