a尺度多小波正交尺度函数及其mallat算法

张臣国，丁昌华

(电子科技大学数学科学学院，成都610054)

0 引言

随着小波分析的发展日益成熟，其应用也越来越广泛，它的理论与算法也研究得越来越深入.由于2尺度小波的构造与mallat分解已成熟［1］，如出现了由I.Daubcchies构造的一系列正交小波，而用a尺度小波分解信号可以得到更好的分辨率，灵活性更大，所以a尺度小波理论的研究也越来越重要，特别是正交多小波同时具有正交、对称、紧支等特点，研究a尺度正交多小波更具有重要意义［2-5］.1996年Chui和Lian利用对称性给出了2重多尺度函数和多小波，杨守志等人给出了几种多小波的构造方法.正交多尺度函数的构造方法有很多，此处基于一特殊的尺度函数，构造出正交多尺度函数，对正交尺度函数的构造有一定的价值.a尺度多小波Mallat算法对信号的分解和去噪等分辨率更高，去噪效果更好，具有一定的研究意义.

1 a尺度多分辨分析

定义1［1］Hilbert空间L2(R)中的一列闭子空间{Vj}j∈Z称为一个a尺度(a＞1，a∈N+)正交多重多分辨分析，若满足:

1)Vj⊆Vj+1(j∈Z).

2)f(t)∈Vj⇔f(at)∈Vj+1.

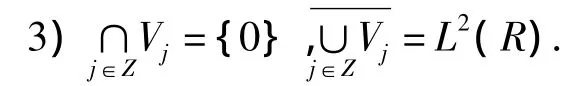
4)存在 r个函数 φ1(t)，φ2(t)，…，φr(t)，使{φυ(t－ k)，k∈Z，1≤υ≤r}为 V0的一个标准正交基，其中φ(t)=(φ1(t)，φ2(t)，…，φr(t))T为 a 尺度正交多分辨分析的尺度函数，∀k，j∈Z.

定义Wj，j∈Z为Vj在 Vj+1中的正交补，即 Vj+1=Vj+Wj，由小波分析理论可知存在 ψ(t)=(ψ1(t)，ψ2(t)，…，ψ(a－1)r(t))T，ψi(t)，i=1，2，…，(a －1)r，它们的伸缩与平移构成 W0的一个标准正交基，称 ψ(t)为正交多小波.所以:1≤υ≤(a －1)r，k∈Z］，j∈Z.于是 φ(t)，ψ(t)满足两尺度关系:

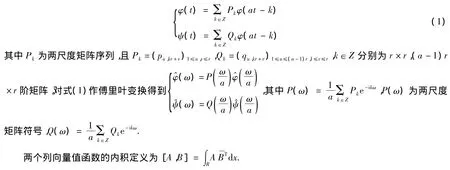
定义 2［2］称 φ(t)=(φ1(t)，φ2(t)，…，φr(t))T与 φ(t)=(φ1(t)，φ2(t)，…，φr(t))T为 a 尺度 r重正交多尺度函数，若满足［φ(t)，φ(t－n)］=δ0nIr，n∈Z，ψ(t)=(ψ1(t)，ψ2(t)，…，ψ(a－1)r)T与ψ(t)=(ψ1(t)，ψ2(t)，…，ψ(a－1)r)T为相应于 φ(t)的正交小波函数，若满足:

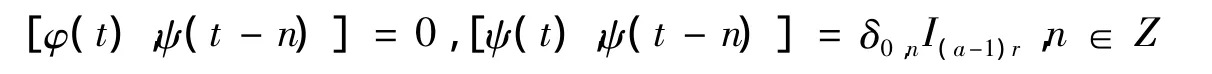
其中0 为 r×(a－1)r阶零矩阵，I(a－1)t为(a－1)r阶单位阵.

2 多小波正交尺度函数构造

引理 1［1，6，7］设φ =(φ1，φ2，…，φr)T，φ1，φ2，…，φr∈L(R)2，则{φl(x － k):1≤l≤r，k∈Z}是一个正交族的充分必要条件是

引理2 设φ是a尺度r重正交尺度函数，P(z)为两尺度符号ωj，j=1，2，…，a为za－1=0的a个根，则，等价于两尺度矩阵序列满足

证明 由引理1和两尺度方程可得

由命题1及引理2就可以得到命题2，构造一种较特殊的正交尺度函数.

3 a尺度正交多小波的mallat算法

定义投影算子:

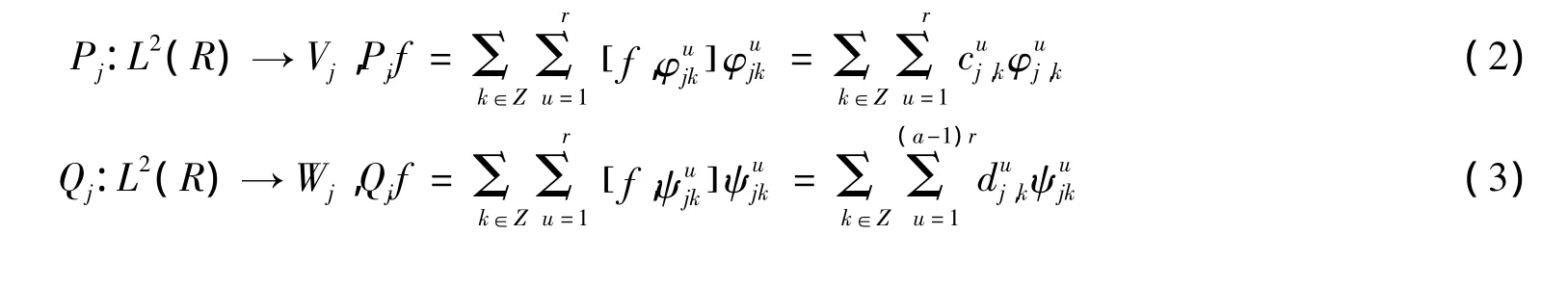
命题3 设投影算子Pj，Qj的定义如式(2)(3)，则有下面的mallat快速算法.

［1］关履泰.小波方法与应用［M］.北京:高等教育出版社，2007

［2］BAUSSARD A，NICOLIER F，TRUCHETET F.Rational multiresolution analysis and fast wavelet transform:application to wavelet shrinkage denosing［J］.Signal Processing，2004，84:1735-1747

［3］BRUNI V，VITULANO D.Combined image compression and denoising using wavelets［J］.Signal Processing:Image Communication，2007，22:86-101

［4］CUI L H，CHENG ZH X.Algorithm of Construction for Orthogonal Multiwavelets with Short Supports from a Given Multiscaling Function［J］.Journal of Xian jiaotong University，2003，37(2):211-214

［5］LENG J S，FU Y D，ZHONG SH M.Algorithms of Decomposition and Reconstruction with Biorthogonal Multiwavelet Packets with Scale［J］.Journal of University of Electronic Science and Technology of China，2006，35(5):851-853

［6］程正兴，杨守志，冯晓霞.小波分析的理论、算法、进展和应用［M］.北京:国防工业出版社，2007

［7］杨守志.a尺度正交多尺度函数和正交多小波［J］.数学物理学报，2005，25A(6):38-40

［8］冷劲松.α尺度多重双正交小波包［J］.工程数学学报，2001，18(s1):125-130

［9］FENG A，ZHANG X，DENG C X.Construction of Compactly Supported Symmetric Orthonormal Multi-wavelet［J］.Journal of Harbin University of Science and Technology，2009，14(3):75-78

［10］LIAN J .Orthog onal criteria for multiscaling functions［J］.Appl Comp Ham Anal，1998(5):277-311