双三相分数槽电动机绕组系数分析与计算

齐 歌，李景丽，周理兵，师 黎

1.郑州大学，河南郑州 450001;2.华中科技大学，湖北武汉 430074)

0 引 言

在交流电动机中，每极每相槽数为分数的绕组被称作分数槽绕组。分数槽绕组解决了电动机较多极数与有限槽数之间的矛盾，并可以通过其等效分布作用削弱电动势和磁动势的谐波，提高其正弦性，并提高绕组利用率，改善电动机性能［1］。鉴于以上诸多优点，近年来分数槽绕组广泛应用于各种电机中［2－5］，满足多种应用的需求。比如分数槽电机可以采用较多的极数，应用于需要低速运转的场合［6］，还可以在设计上减小电机槽数与极数之间的周期，适用于要求低转矩脉动的场合［7］。分数槽电机广泛应用于风力发电、起重装置和电动汽车［8］等直接驱动场合，并且在要求较高的容错性能的领域也有运用［9］。

近些年来，集中非叠绕组经常应用到分数槽电机中［10－12］。在这种绕组形式中，每个线圈只缠绕在电机的一个齿上，各个线圈端部之间没有重叠，不容易发生匝间短路，同时线圈周长和绕组端部伸出长度均有所减少，进而节省用铜量。此外，采用这种绕组形式下线简单，可以使用专用绕线设备，节省人工，提高工效。

鉴于分数槽集中非叠绕组的诸多优点和广泛的应用前景，本文把这种绕组形式应用到双三相电动机中，分析了不同极槽配合下的绕组系数。在参照传统三相分数槽电动机极槽配合与绕组系数计算的基础上，归纳出了双三相分数槽集中非叠绕组电动机的绕组系数在极槽配合影响下的变化规律，并总结出计算公式，供电机设计以及性能分析时作参考。

1 绕组系数计算

绕组系数是电机性能计算中的一个重要参数，它是既考虑线圈短距的影响，又考虑绕组分布时整个绕组的合成电动势所打的总折扣。电机中，不同的极、槽数和绕组排列方式可以获得不同的绕组系数。通常，为了使电机具有更大的反电动势和电磁转矩，需要尽可能高的绕组系数。绕组系数kwn等于线圈短距系数kpn和绕组分布系数kdn的乘积［13］:

式中:n表示谐波次数。

短距线圈是指线圈的节距小于电动机极距的线圈，其节距用电角度γ表示。短距线圈能有效地抑制谐波电动势，因此在交流绕组中广为采用。短距系数的定义为短距线圈的电动势与整距线圈电动势的比率，其大小可由下式求得:

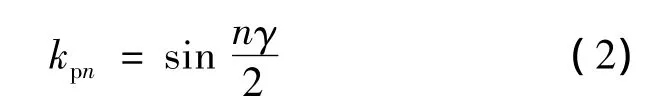
分布绕组是指组成一相绕组的线圈嵌放在不同槽内，按照一定的规律连接起来，线圈的空间位置互不相同。绕组分布系数的定义为属于同一相绕组的各个线圈的电动势的相量和与算数和之比率。绕组分布系数可以通过画出槽相量星形图得知。如果一相绕组由i个嵌放在不同槽内的线圈串联组成，每个线圈在空间上依次相邻σ电角度，则绕组分布系数的大小可由下式求出:

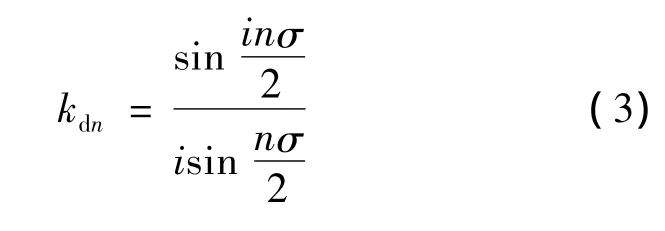
2 三相分数槽电动机不同极槽配合下绕组系数分析

2.1 三相极槽配合

在三相分数槽电动机中，为了获得更高的绕组系数，除了运用可以得到高绕组分布系数的绕组排列之外，通常使电动机的槽数Q尽可能地接近极数2p，以便获得更高的短距系数。根据分析，在实际应用中最常用的是2p=Q±2这种极槽配合。极槽配合为2p=Q±1的三相电动机虽然具有更高的绕组系数，但由于定子槽和定子线圈的不对称分布使得电机存在严重的不平衡力［14］，减少轴承的使用寿命，并增大振动和噪声，降低了电动机的性能。因此，本文以2p=Q±2这种极槽配合为对象，分析三相分数槽电动机采用集中非叠绕组且槽数不超过30时的不同极槽配合，计算了相应的最大基波绕组系数，如表1所示。

通过分析表中数据可以总结出:

(1)构成三相电动机的基本条件为:电机槽数是相数3的整数倍;

(2)构成2p=Q±2极槽配合的条件为电机槽数为相数3的偶数倍;

(3)在满足2p=Q±2这种同一关系的极槽配合中，槽数越大，绕组系数越高。

分数槽电动机的基波绕组系数

表1 极槽配合满足2p=Q±2时三相

2.2 三相绕组系数计算

表1中的基波绕组系数都是通过式(1)～式(3)计算而来的。通过式(2)可以看出，绕组的短距系数仅仅与线圈的节距有关，而线圈的节距可以由线圈的两个边所跨越的电角度γ表示。对于集中非叠绕组，每个线圈只缠绕在一个电机齿上，其节距就等于一个齿距也即一个槽距，于是有:

因此集中非叠绕组的短距系数可以通过下式计算而得:

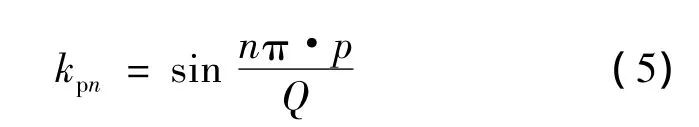
从式(5)可以进一步得出，集中非叠绕组的短距系数仅仅与电动机的极、槽数有关，一旦确定了电动机的极、槽数，其短距系数就随之确定了，不受绕组形式的影响。由此可见，对于已经确定极、槽数的电动机而言，其短距系数为固定值，只能通过增大绕组分布系数来提高整体的绕组系数。

绕组分布系数计算式中的参数i和σ，需要通过画出电机的槽电动势星形图来确定。这种方法繁琐而不直观。意大利学者 Bianchi［15］对其进行简化，总结出一个只需利用电动机的极、槽数来直接求取最大绕组分布系数的计算公式:

式中:m是电动机的相数;t是电动机的槽数Q和极对数p之间的最大公约数，表示电动机可以分为t个槽数为(Q/t)，极对数为(p/t)的单元电动机;qph是单元电动机槽相量星形图中组成同一相的相量个数;αph则是这些相量中相邻两相量之间的夹角。

3 双三相分数槽电动机不同极槽配合下绕组系数分析

绕组系数由短距系数和分布系数相乘而得。通过前面的分析已经知道，绕组的短距系数仅仅由电动机的极、槽数决定，与采用何种绕组形式无关，因此双三相集中非叠绕组仍然可以通过式(5)计算绕组的短距系数。

绕组的分布系数会受不同的相绕组排列方式影响，需要借由画出具体的槽相量星形图确定。在三相电动机的研究中，Bianchi总结出计算公式，可以省略槽相量星形图，方便、直观地求出绕组分布系数，方便他人在分析计算电机参数和性能时运用。然而，这套在三相电动机中应用成熟的公式却并不适用于双三相电动机。式(8)中定义的整数qph表示单元电动机中一相的相量个数，而对于部分双三相电动机来说，其值为分数，已经失去意义。因此，本文把Bianchi的思想引入到双三相电动机中，试图通过探寻绕组分布系数计算参数i和σ与双三相电动机的槽数、极数和相数之间的关系，归纳总结出一套类似的适用于双三相电动机绕组分布系数计算的公式。

3.1 双三相极槽配合

双三相电动机采用不同极槽配合时所能获得的最大绕组系数，如表2所示。为简便起见，表中只列出了极、槽数均不超过30的情况。通过对表中数据

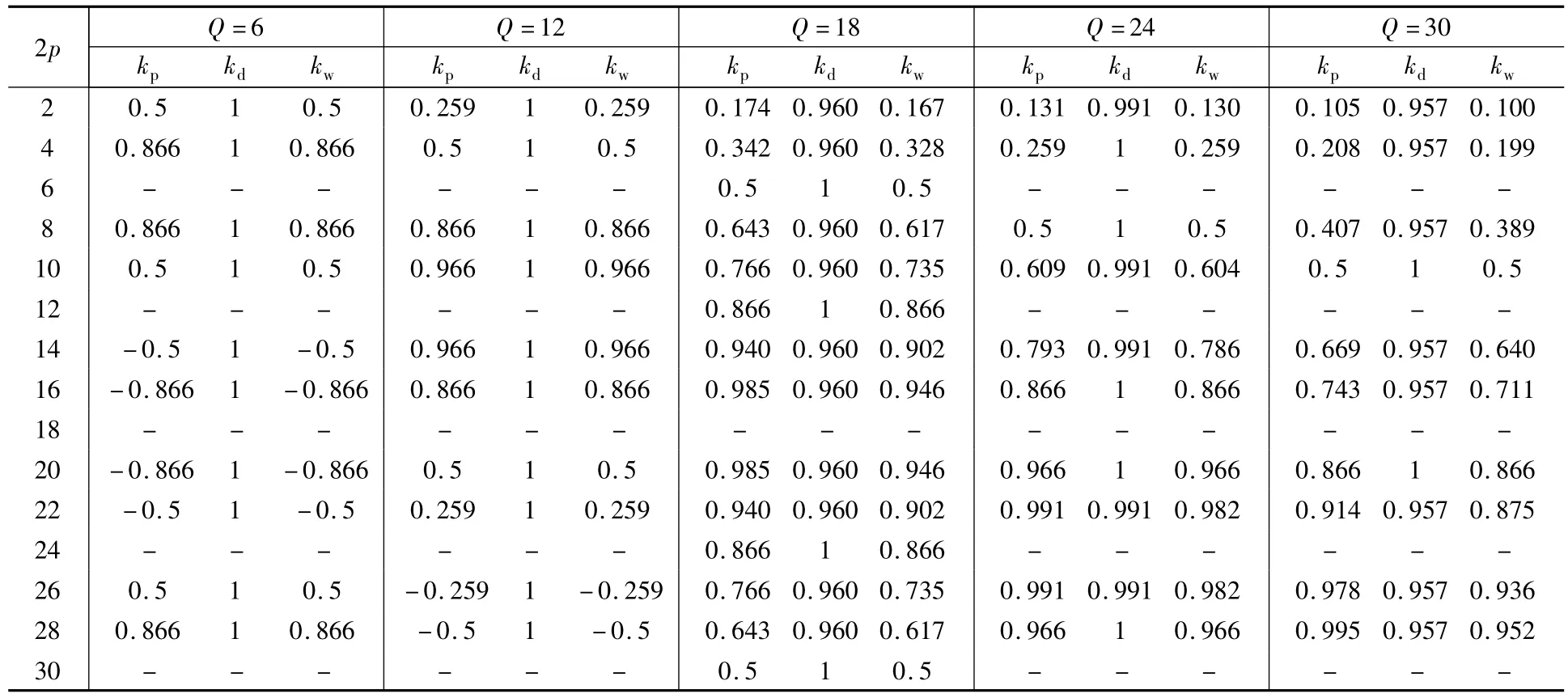
表2 集中非叠绕组双三相电动机在不同极槽配合下的绕组系数

进行分析，可以得到以下结论:

(1)构成双三相电动机的基本条件:电机槽数是相数6的整数倍，而且槽数与极数的差值只能为偶数:

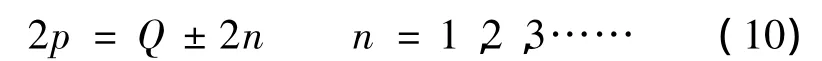
(2)构成双三相电动机有效极槽配合的约束条件:

(3)与三相电动机的规律一致，双三相电动机的极槽配合也符合对角线原则。即表中对角线处的极槽配合(满足2p=Q±2)可以获得最大的绕组系数，并且极槽配合越接近对角线，其绕组系数也越大。此外，当双三相电动机槽数和极数的差值相等时，其绕组系数也一样，在表中沿对角线呈对称分布。

(4)在极槽配合为2p=Q±2的三相电动机中，绕组系数随着槽数的增加而增大，但是双三相电动机却不同。双三相绕组由两套三相绕组构成，当两套三相绕组之间的夹角为30°电角度时，整个绕组的分布系数增大为1(如12槽10极)，进而增大总的绕组系数，这也是双三相绕组的一大优势。

(5)双三相电动机具有相同的单元电机时，其绕组系数也相同。这同样和三相电动机的规律一致。

3.2 双三相绕组分布系数计算

双三相电动机采用不同极槽配合时的绕组分布系数及其相应的计算参数，如表3所示。通过分析发现，与三相电动机类似，双三相电动机在计算绕组分布系数时所用的参数i和σ仍旧与电动机的槽数、极数和相数有关，存在着一定的规律性:

(1)在kd=1的极槽配合中，极数2p均为的整数倍;

(2)在kd≠1的极槽配合中，当是奇数时，i=，σ=;当是偶数时，i=，σ =。

根据上面的规律，在已知电动机的槽数、极数和相数的情况下，不需要考虑具体的绕组排列形式，也即省去分析槽相量星形图的过程，就可以直接通过公式计算出双三相电动机的绕组分布系数。公式总结如下:

式中:m为双三相电动机的相数;Q为双三相电动机的槽数;p为双三相电动机的极对数。经验证，以上公式适用于双三相电动机所有的极槽配合。

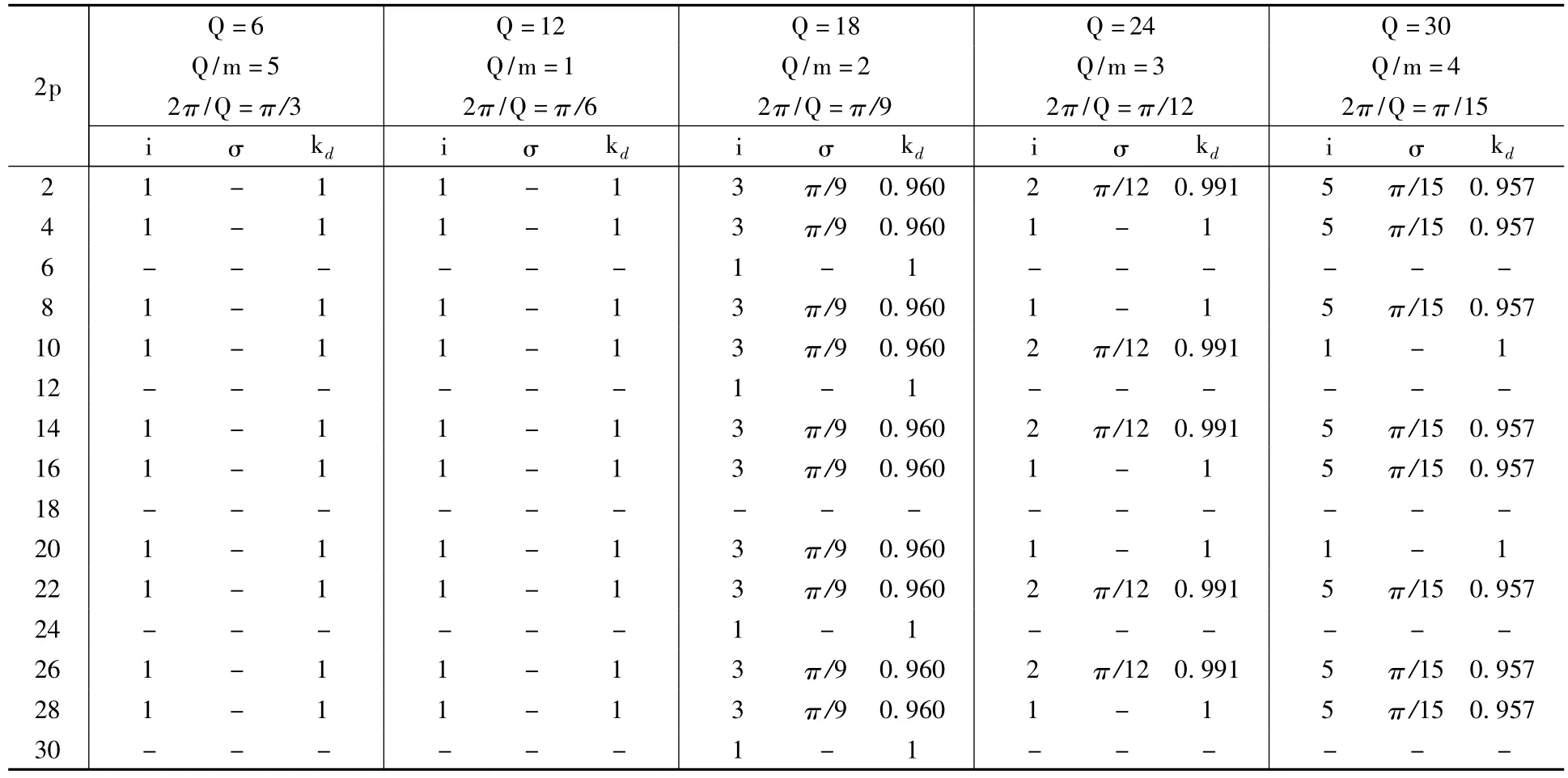
表3 双三相电动机不同极槽配合下的绕组分布系数及其相应计算参数(m=6)

4 结 语

分数槽集中非叠绕组由于其具有许多优点而广泛应用于各种电机中。本文对双三相分数槽集中非叠绕组电动机进行研究，分析了不同的极槽配合及其相应的绕组系数。首先介绍了绕组系数的一般计算方法，并系统分析了传统三相分数槽电动机的常用极槽配合，计算了其绕组系数。针对绕组的分布系数需要通过画槽电动势星形图得出，计算十分麻烦，本文进一步介绍了意大利学者总结出的适用于三相电动机的绕组系数计算公式。然而这套公式对于双三相电动机并不适用。因此，在参照传统三相分数槽电动机极槽配合分析与绕组系数计算的基础上，本文归纳出了双三相分数槽集中非叠绕组电动机的绕组系数在极槽配合影响下的变化规律，分析计算了绕组系数，并总结出计算公式，方便他人在电动机设计过程以及性能分析中的应用。

［1］谭建成.三相无刷直流电动机分数槽集中绕组槽极数组合规律研究［J］.微电机，2007，40(12):72－77，86.

［2］El－ Refaie A M，Zhu Z Q，Jahns T M，et al.Investigation of winding inductances in fractional slot surface－mounted permanent magnet brushless machines［J］.IEEE Industry Applications Society Annual Meeting，2008:1 －8.

［3］Bianchi N，Bolognani S，Pre M D，et al.Design considerations for fractional－slot winding configurations of synchronous machines［J］.IEEE Transactions on Industry Applications，2006，42(4):997－1006.

［4］Ishak D，Zhu Z Q，Howe D.Rotor eddy current loss in PM machines with fractional slot number per pole［J］.IEEE Transactions on Magnetics，2005，41(9):2462 －2469.

［5］Chen Y S，Zhu Z Q，Howe D.Vibration of permanent magnet brushless machines having a fractional number of slots per pole［J］.IEEE Transactions on Magnetics，2006，42(10):3395 －3397.

［6］Salminen P，Niemela M，Pyrhonen J，et al.Performances analysis of fractional slot wound PM－motors for low speed applications［C］//Conf.Rec.IEEE 39th IAS Annu.Meeting.IEEE，2004(2):1032－1037.

［7］Bianchi N，Bolognani S.Design techniques for reducing the cogging torque in surface － mounted PM motors［J］.IEEE Transactions on Industry Applications，2002，38(5):1259 －1265.

［8］Bianchi N，Bolognani S，Grezzani G.Fractional－ slot IPM servomotors:analysis and performance comparisons［C］//Proceedings of the International Conference on Electrical Machines.Cracow，Polomd，2004:1 －6.

［9］Bianchi N，Pre M，Grezzani G，et al.Design considerations on fractional－ slot fault－ tolerant synchronous motors［C］//IEEE International Conference on Electric Machines and Drivers.San Antonio，US，2005:902 －909.

［10］Wrobel R，Mellor P.Design considerations of a direct drive brushless machine with concentrated windings［J］.IEEE Transactions on Energy Conversion，2008，23(1):1－8.

［11］Bianchi N，Bolognani S，Pre M D.Magnetic loading of fractionalslot three － phase PM motors with non － overlapped coils［J］.IEEE Transactions on Industry Applications，2008，44(5):1513－1521.

［12］El－ Refaie A M，Jahns T M，Novotny D.Analysis of surface PM machines with fractional－ slot concentrated windings［J］.IEEE Transactions on Energy Conversion，2006，21(1):34－43.

［13］汤蕴璆，史乃.电机学［M］.北京:机械工业出版社，1999.

［14］Zhu Z Q，Ishak D，Howe D，et al.Unbalanced Magnetic Forces in Permanent－Magnet Brushless Machines with Diametrically Asymmetric Phase Windings［J］.IEEE Transactions on Industry Applications，2007，43(6):1544 －1553.

［15］Bianchi N.Teory and design of fractional－ slot PM machines［M］.CLEUP，2007.