基于变结构自抗扰控制器的永磁同步电动机伺服系统

周腊吾，严 伟，匡江传

(湖南大学，湖南长沙 410082)

0 引 言

永磁同步电动机(以下简称PMSM)因其高功率密度、高转矩电流比、低损耗等优点［1］而被广泛应用于高精度数控机床、印刷、机器人等位置控制系统中;然而作为一个典型的非线性复杂控制对象，其模型具有多变量耦合等特点;系统自身控制参数变化及负载未知变化会影响系统控制精度，要实现对电机高精度的位置控制，必须消除此干扰。

常规控制方法一般采用PID控制［2］，其算法简单、易于实现，能满足一定范围内的控制要求，但其克服自身及系统外部扰动性能方面较弱，控制精度不高。复杂控制方法有逆系统控制［3－4］、自适应控制［5－6］和滑模控制［7－8］等方法，都需已知被控对象模型和扰动模型，且对参数依赖性强、系统鲁棒性差。智能控制［9－10］无需知道被控对象的精确模型，对系统扰动鲁棒性好，但算法复杂、控制系统成本较高。

本文提出了一种PMSM变结构自抗扰位置伺服控制系统。将变结构控制(VSC)引入到位置自抗扰控制器(ADRC)的设计中，通过对控制器中扩张状态观测器(ESO)和非线性状态误差反馈控制律(NLSEF)的变结构改进，既保持了原控制器特点，又减少了可调参数，并改善了系统控制性能;结合位置环、转速环和电流环，设计了一种新的变结构自抗扰位置控制器，在保证系统动态性能的同时，提高了系统鲁棒性。仿真结果表明，改进后的系统具有响应速度迅速、无超调、稳态精度高，对负载及系统扰动鲁棒性强的特点。

1 PMSM的数学模型

PMSM d－q坐标结构如图1所示。在该坐标中电机转子以同步电角速度ω旋转，假定其空间磁场呈正弦分布，且忽略磁路饱和，不计磁滞和涡流损耗影响，当PMSM转子结构为表贴式时有Ld=Lq=L，在此条件下，采用id=0矢量控制策略时，得到同步坐标系下PMSM的状态方程［11］:

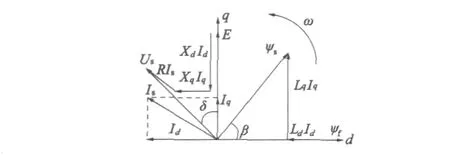
图1 PMSM d－q坐标结构

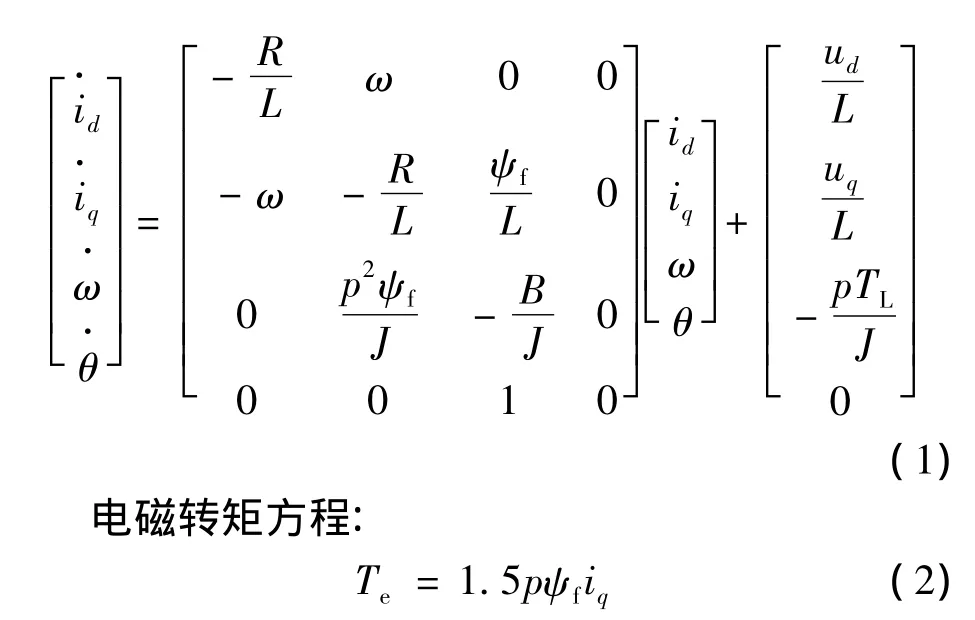
式中:id、iq为电机定子电流 d、q轴分量;ud、iq为定子电压d、q轴分量;ω为转子角频率;R为定子绕组电阻;L为定子d、q轴自感;ψf为转子永磁体产生的磁链;TL为负载转矩;Te为电磁转矩;J为转子转动惯量;B为阻力系数;p为极对数;θ为转子位置角。

2 变结构自抗扰器的数学模型

2.1 自抗扰控制的数学模型

自抗扰控制技术是近几年以来在非线性PID控制的基础上发展而来的一种改进的新型非线性控制技术［12－13］，主要包括跟踪微分器、扩张状态观测器、非线性状态反馈(NLSEF)三部分。

设三阶被控对象的状态方程如下:

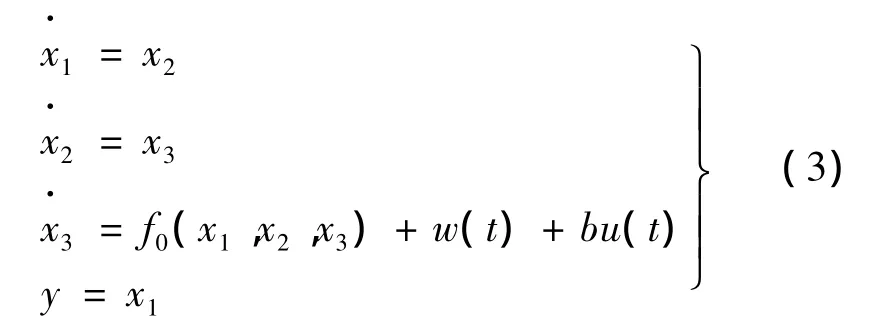
式中:b为系统控制量增益;u(t)为系统控制量;f0(x1，x2，x3)为系统已知部分;w(t)为系统未知部分，此两部分的总和为系统的总扰动。

三阶被控对象的ADRC方程如下:

(1) 线性微分－ 跟踪器

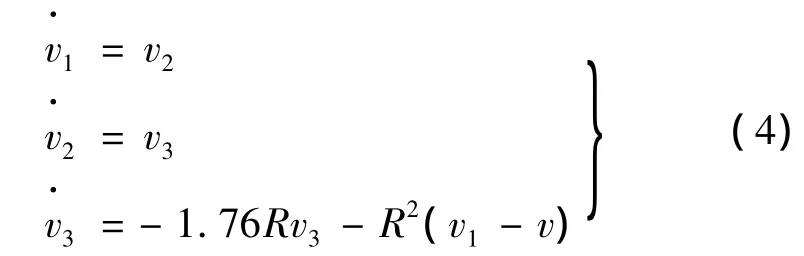
式中:v为输入信号;v1为v的跟踪信号;v2为v1的微分信号;v3为v2的微分信号;R为速度因子，R越大，跟踪速度越快。

(2)非线性扩张状态观测器

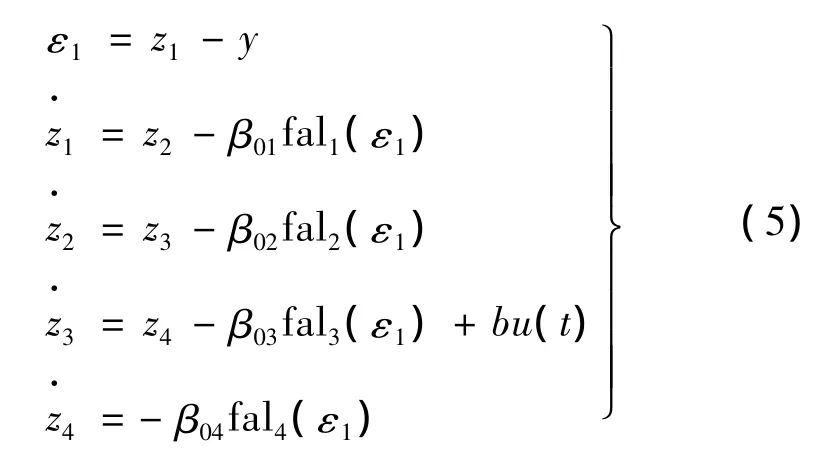
式中:y为系统输出;z1为y的跟踪信号;z2为z1的微分信号;z3为z2的微分信号;z4为系统扰动的跟踪信号;ε1为误差信号;β01、β02、β03和 β04为输出误差校正增益。

(3)非线性状态反馈控制律

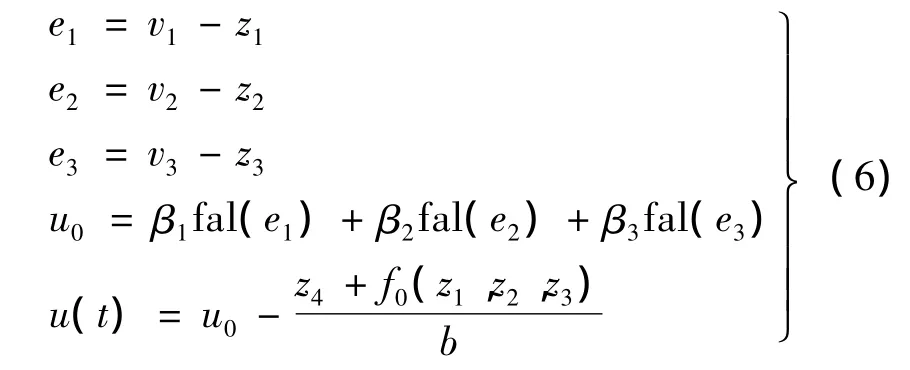
式中:e1、e2和e3分别为误差、微分和二次微分信号;β1、β2和β3分别为误差、微分和二次微分增益;f0(z1，z2，z3)为系统已知部分。

fal(·)为最优综合控制函数，其表达式:

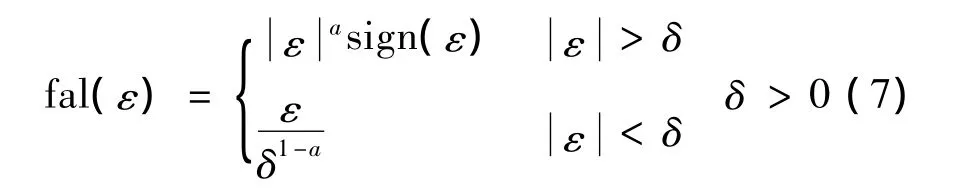
式中:a为非线性因子;δ为滤波因子;ε为输入误差变量;适当选取参数可实现系统性能优良的非线性控制，从而提高了系统控制精度［14］，使控制器具有较强的适应性和鲁棒性。

2.2 变结构扩张观测器的数学模型

变结构控制(VSC)［15］的基本思想是通过控制作用将从系统任一点出发的状态轨迹引导到滑模面，同时保证系统在滑模面上的运动是渐进稳定的，即滑动模态。滑模可达性条件仅保证在有限时间内系统由任意初始状态到达滑模面的要求，而对其具体运动轨迹未做任何限制，运用适当的策略可以改善趋近运动的动态性能。

针对单输入单输出控制系统，设计滑模变结构控制步骤如下:

(1)设计滑模切换函数 s=cx=［c1，c2，…，cn］·［x1，x2，…，xn］T，选取适当的常数 c1、c2、…、cn，使得滑模运动是渐进稳定的。

(2)求取最佳滑动模态趋近控制率u，使得在超平面s=0上的每一点存在滑动模态，且控制作用必须让系统状态进入滑模面。

对式(5)作适当变形，则式(5)与式(8)是等价的［16］:

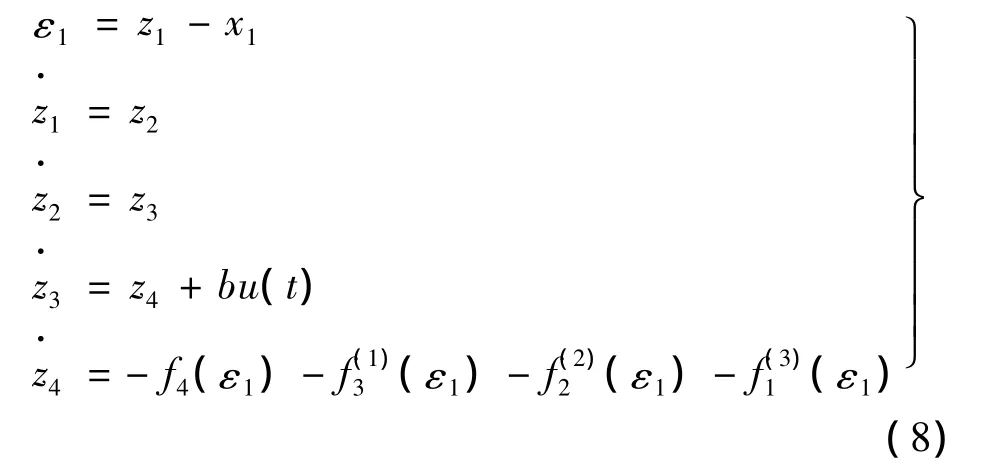
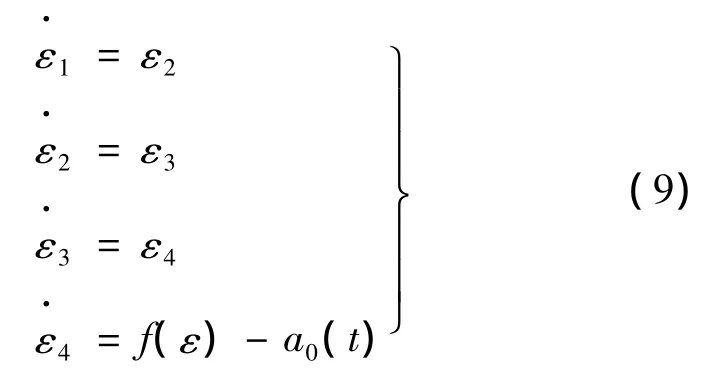
只要选取合适的函数f(ε)就能保证变结构扩张状态观测器式(9)稳定［17］，从而可使式(5)稳定。对于式(9)，取滑模平面函数:

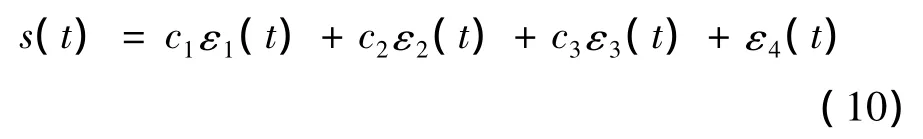
适当选取常 c1、c2、c3，满足多项式 p4+c3p3+c2p2+c1p+1(p为拉普拉斯算子)为赫尔维茨稳定，并使之具有较大的稳定裕度。令函数:

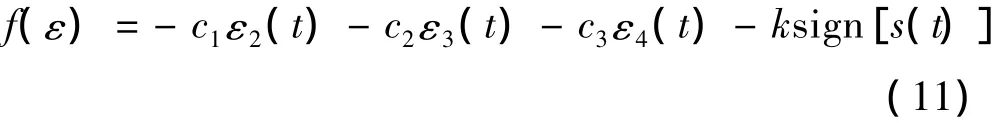
则变结构扩张状态观测器式(9)稳定。式中，sign(·)为符号函数，sign(t)=1 t≥0{0 t＜0，k为可调参数。其证明如下:

对函数s(t)微分，同时将式(9)代入式中，可得:

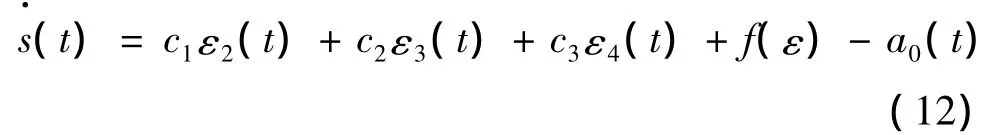
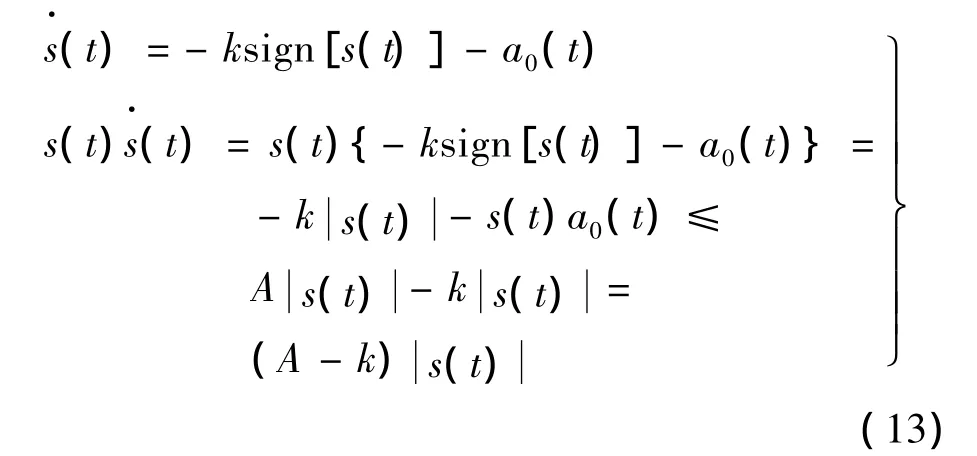
式(13)中，适当选取 k，使 k＞A，则 s(t)(t)≤0，由Lyapunov稳定性定理可知，在此条件下，系统进入滑动模面，从而保证了系统的稳定性。为了减弱抖振，用继电特性函数θ(s)代替式(11)中的符号函数 sign(·)，此函数:θ(s)=，δ 为较小的1正的常数，且可调。

2.3 变结构非线性组合控制器的数学模型

式(4)中，v1为给定信号v(t)安排的过渡信号，v2、v3为这个过渡过程信号的一阶、二阶导数。式(5)中，z1、z2、z3是对系统状态变量的重构，因此两组变量之间的误差 e1=v1－z1，e2=v2－z2，e3=v3－z3为对象参考输入v(t)的状态误差;由于，对非线性误差反馈控制律变形，有:

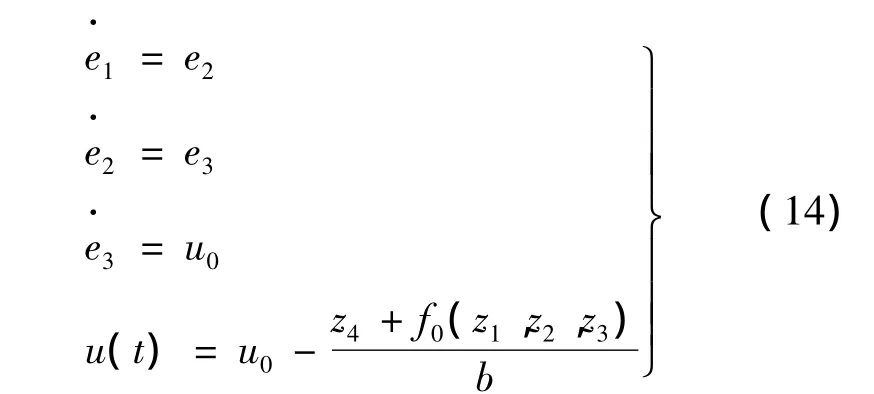
同样地，若取:

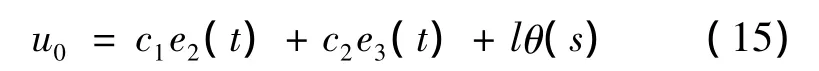
也可保证式(14)稳定。式中，l为可调参数，θ(s)为继电特性函数，以减小系统抖振，其表达式:θ(s)=，δ为较小的正可调参数，常数c、c和滑模212面的取法以及稳定性分析与前所述类似，文中定义误差为输入信号与输出信号的差，故控制作用u0为“正”。

由分析可得，改进后的扩张状态观测器(ESO)与非线性状态误差反馈控制律(NLSEF)各含有两个可调参数，且个数不受被控系统阶次的限制。与改进前相比，控制器的可调参数有所减少，这使得参数整定变得容易。

3 PMSM变结构自抗扰位置控制器

由式(1)可得PMSM位置环在旋转坐标系下的三阶动态方程［14］:

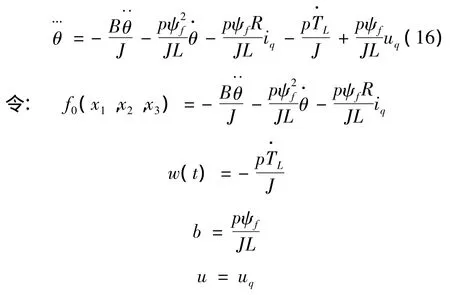
式中:f0(x1，x2，x3)为系统已知扰动，w(t)为系统未知扰动。通过这两项可以有效地估计系统的负载扰动，并对总扰动进行补偿，对负载扰动有很好的鲁棒性;在有位置传感器的条件下，ω为已知量，其微分亦为已知量，可得位置环的状态方程:

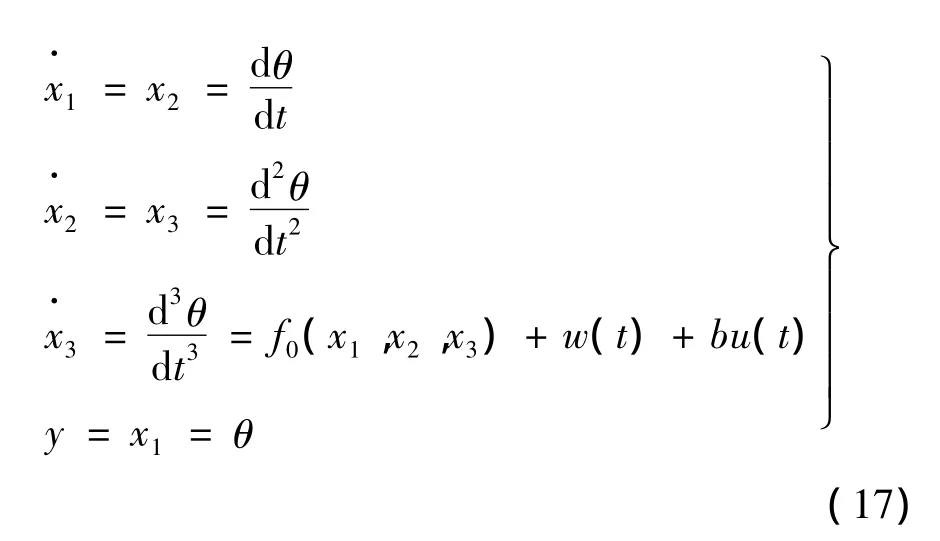
由此可知，其状态方程与式(3)相同。故可依据式(4)、式(9)和式(14)来设计位置环变结构ADRC控制器的各部分，其结构如图2所示。图中，θ*是给定转子位置是给定q轴电压，θ为转子实际位置信号，v1是给定位置信号的跟踪，v2、v3为位置给定的微分、二次微分信号，z1为转子实际位置的跟踪，z2为跟踪的微分，z3为z2的微分信号，z4为系统不确定部分观测量，即 w(t)、f0(z1，z2，z3)为已知部分观测量，此处的微分不同于PD控制的微分，它对“噪声”不是起放大作用，而是起抑制作用［18］。

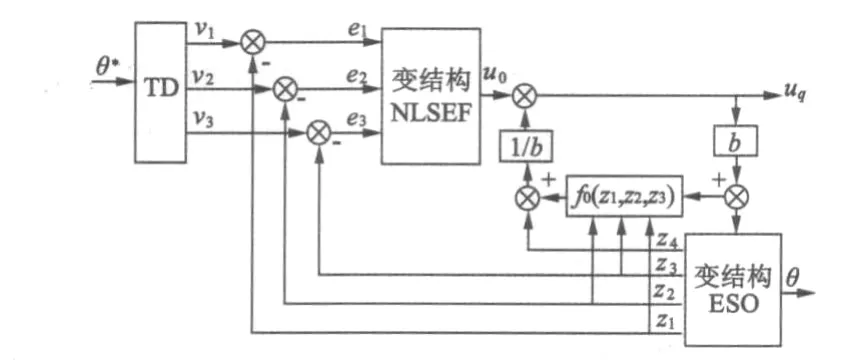
图2 变结构自抗扰控制器的总体框图

此控制器中，跟踪微分器(TD)对θ*进行滤波，通过TD作用，可得到平稳的跟踪信号v1，并获得其一次、二次微分信号v2、v3，可使系统响应迅速并无超调。通过变结构扩张观测器作用，不但能得到各参变量的观测值，且能获得系统干扰的观测值，比如:电机定子电阻、电感以及转子惯量变化的干扰以及负载变化等其它未知扰动。通过变结构非线性组合控制器，不但可以补偿系统的各种扰动，而且能对位置信号实现性能优良的非线性控制，改进后的控制器即保持了原有特点又减少了可调参数，并改善了系统性能，提高了位置伺服系统的控制精度。

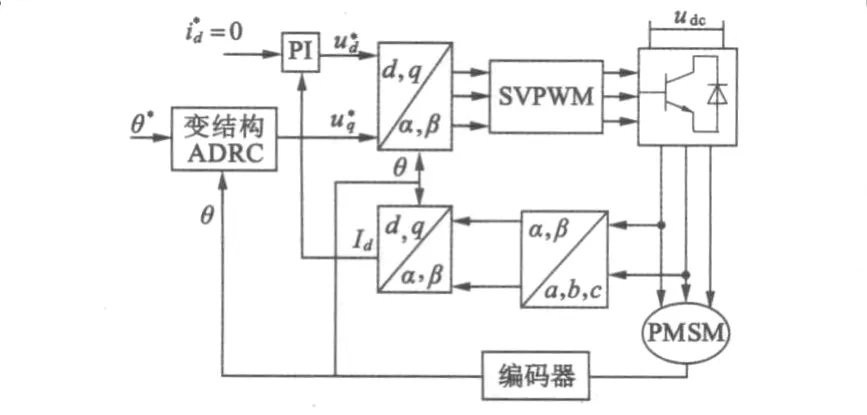
图3 PMSM位置伺服系统控制结构图

PMSM位置伺服系统结构图如图3所示，该系统采用采用id=0的双环矢量控制结构，即位置环和电流环。位置环是将位置环、速度环和q轴电流环综合在一起而形成的一种新的控制器;d轴电流环采用传统的PI调节器。与传统控制结构相比，不仅减少了控制环节，优化了控制策略，而且增强了整个控制系统抗扰性，提高了系统稳定性。

4 仿真结果分析

为验证采用变结构自抗扰伺服控制系统方案的性能，本文对其进行了仿真。永磁同步电动机参数如下:额定功率PN=1.82 kW，额定转速n=6000 r/min，定子电阻 R=1.63 Ω，交轴、直轴分别为 Ld=Lq=5.3 mH，转动惯量为 J=0.00109 kg·m2，极对数为p=2，额定转矩Te=7 N·m，转子磁通ψ=0.304 Wb，fN=200 Hz。位置环周期为 0.1 ms。

仿真过程中选取参数为:R=106，δ1=0.05，δ=0.025，k=30，l=25。其结果如下:给定位置为0.0001 rad、空载起动、电机在0.5 s施加额定负载，其结果如图4所示。此系统位置控制准确，且稳态跟踪精度高，无超调，对负载扰动鲁棒性强。

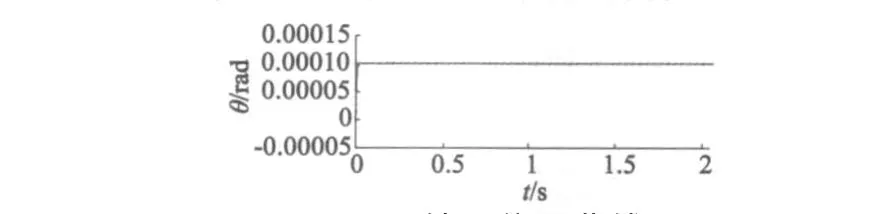
图4 转子位置曲线

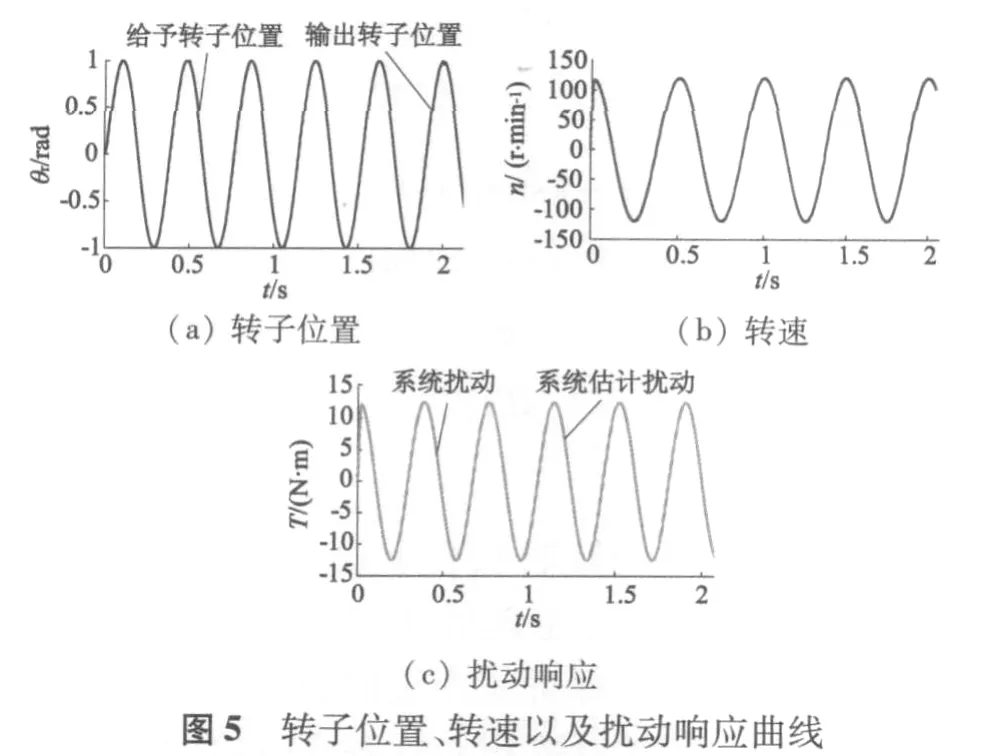
给予转子位置按照1*sin(2t)变化，同时负载按照7.5*sin(2t)扰动，电机转子位置、实际转速和系统扰动结果如图5所示。图中，PMSM位置跟踪准确且精度高;转速为位置的微分，它除了在起动的瞬间有极小的脉动外，在稳态时，响应平稳，无脉动;VS－ADRC位置控制器观测出的负载扰动与真实值基本接近。

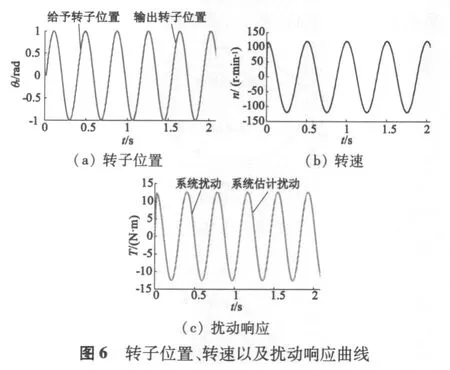
位置信号和负载扰动曲线同上，电机转子惯量和定子电阻为原来的2倍，转子位置、实际转速和系统扰动结果如图6所示。由图6可得，电机参数变化后，并没有影响位置响应，其仍旧能对给定位置精确跟随，而转速和系统扰动只是在电机起动时有微小的脉振，稳态响应与参数变化前相同。

5 结 语

本文将自抗扰与变结构控制原理相结合，形成了一种新的变结构自抗扰控制器并将其运用于PMSM位置伺服系统中。改进后的控制器可调参数减少并大大改善系统的控制性能。由仿真结果可知，系统改进后其动态响应迅速且无超调，控制精度高，稳态误差小;并且对系统负载及转动惯量等内外扰动有很强的抗扰能力。

［1］唐任远.现代永磁电机理论与设计［M］.北京:机械工业出版社，2008.

［2］Marco T，Francesc P，Zhang Daqing.Real－ time gain tuning of PI controllers for high － performance PMSM drivers［J］.Trans.on Industry Applications，2002，38(4):1018 －1026.

［3］杨立永，李华德，王久和.基于逆系统理论的感应电动机控制策略［J］.辽宁工程技术大学学报，2005，24(5):706 －708.

［4］张兴华，张骥.永磁同步电动机逆系统解耦控制［J］.微电机，2007，40(5):9 －12.

［5］宋亦旭，王春洪，尹文生，等.永磁直线同步电动机的自适应学习控制［J］.中国电机工程学报，2005，25(20):151 －156.

［6］Li Weiping，Cheng Xu.Adaptive high precision － control of positioning tables－ theory and experiments［J］.IEEE Trans.on Control Systems Technology，1994，2(3):265－270.

［7］瞿少成，姚琼荟，李槐树.正弦波型直流无刷电动机位置伺服系统的变结构控制［J］.海军工程大学学报，2000，5(6):20－24.

［8］张昌凡，王耀南，何静.永磁同步伺服电机的变结构智能控制［J］.中国电机工程学报，2002，22(7):13 －17.

［9］Wan Wenbin，Zhang Xuedian，Xu Jiaqun，et al.A Feed － forward Control System of PMSM Based on Artificial Neural Network［C］//The Fifth International Conference on Electrical Machines and Systems.2004，2(6):679 －682.

［10］Yang Yi，Vilathgamuwa D M，Rahman M A.Implementation of an Artificial－ Neural－ Network－ Based Real－Time Adaptive Controller for an Interior Permanent Magnet Motor Drive［J］.IEEE Trans.on Industry Applications，2003，39(1):96 －104.

［11］Pillay P，Knshnan R.Modeling of Permanent Magnet Motor Drives［J］.IEEE Transactions On Industrial Electrics，1988，35，(4):537－541.

［12］韩京清.自抗扰控制器及其应用［J］.控制与决策，1998，13(1):19－23.

［13］黄一，张文革.自抗扰控制器的发展［J］.控制理论与应用，2002，19(4):485 －492.

［14］孙凯，许镇琳，盖廓，等基于自抗扰控制器的永磁同步电机位置伺服系统［J］.中国电机工程学报，2007，27(15):43－46.

［15］刘金琨.滑模变结构控制MATLAB仿真［M］.北京:清华大学出版社，2005.

［16］韩京清.自抗扰控制技术［J］.前沿科学，2007，1(1):24－31.

［17］陈刚，张兆靖，杨慧中.基于变结构的自抗扰控制器［J］.化工自动化及仪表，2007，34(6):16 －19.

［18］韩京清.非线性PID控制器［J］.自动化学报，1994，20(4):487－490.