交通荷载对拉索钢丝疲劳寿命的影响

徐 俊，古 锐，于振华

（同济大学 土木工程学院，上海 200092）

斜拉桥是一种主要的大跨度桥型，拉索作为该桥型中主要承力构件，担负着将主梁上的荷载传递到桥塔上的任务.拉索结构十分纤细，是斜拉桥结构体系中对病害最敏感的构件.在交通荷载往复作用下，斜拉索内的应力也是循环作用的，并在拉索内累积疲劳损伤，甚至导致钢丝断丝，拉索破坏，严重威胁斜拉桥运营安全.大量研究表明，往复交通荷载作用是导致拉索疲劳破坏的主要原因之一.

常用的疲劳寿命分析方法有两种，分别是基于疲劳曲线和线性损伤累积法则（如Miner线性积伤准则）的传统疲劳分析方法，以及基于裂纹扩展分析的断裂力学方法.传统方法已经诞生了近一个世纪，相关研究较为成熟，但这种方法需要明确加载历史，以及与结构实际状态相配的疲劳曲线，这两大难点往往导致分析精度较低.Fisher最早尝试将断裂力学方法引入桥梁的疲劳寿命分析中，该方法依据裂纹扩展至根据材料断裂韧性算得的临界裂纹长度的时间来推测构件的疲劳寿命［1］.裂纹扩展性能可以采用标准试件进行疲劳加载获取，裂纹扩展速率的实验成本低，降低了材料不确定性对疲劳寿命分析的影响，提高了分析精度；同时以无损检测确定的初始裂纹（缺陷）作为结构当前损伤程度的评价标准，无需了解加载历史，且分析结果可以通过探伤进行修正与更新.随着相关理论的发展，更多的学者认识到了这种方法的优点［2］，如今其已成为研究桥梁疲劳寿命一种可靠方法.

在基于断裂力学的疲劳寿命分析中，许多参数的不确定性都对计算结果的可靠度有着较大影响，包括初始裂纹形状、材料参数、几何尺寸、裂纹扩展模型及参数.为了研究这些参数不确定性对疲劳寿命分析的影响，有关专家学者在该领域内开展了大量的研究工作.这些研究涉及初始裂纹的概率分布［3－5］、检出概率［6－7］、材料参数以及模拟方法［8－9］等.此外，交通荷载效应的影响也十分显著.为了分析交通荷载效应，Xing J等［10］和 Huang X等［11］分别假设应力幅服从对数正态分布和威布尔分布，通过理论推导和数值模拟研究了交通荷载的影响.Barson J M［12］采用试验方法研究了应力幅周期性单调降低、周期性单调增加、周期性先单调增加再单调降低，以及常幅4种加载方式对桥梁钢构件的影响.但他的这些假设并不能涵盖应力谱的所有类型.为了更全面地研究交通荷载效应对拉索疲劳寿命的影响，本文尝试从以下两个方面进行分析：

（1）交通荷载应力谱的概率分布规律及其对疲劳寿命的影响.

（2）交通荷载峰值对临界裂纹长度的影响.

为简化计算，分析中将恒载效应、材料参数以及钢丝裂纹断面形状影响等均假定为常值.以周为基本时间单位对交通荷载效应进行统计.

现代交通荷载通过动态称重（weigh in motion，WIM）技术可以提供包括轴重、轴距、轴数、车型、车辆横向位置、车速等交通流量特性，为交通调查提供了便利.交通荷载效应由WIM系统所记录的交通荷载流加载于拉索的不同车道影响线上累加得到.

1 交通荷载分布对裂纹扩展的影响分析

断裂力学理论发展至今，已提出了许多经典的裂纹扩展模型，如 Paris公式［13］，Foreman公式［14］，和Weertman公式［15］.研究中采用应用最普遍也最简单的Paris公式进行分析.

式中：a为裂纹长度；N为荷载循环次数；C和m 为与材料相关的疲劳常数（通常由试验确定）；ΔK为应力强度因子幅，由下式确定：

式中：σ为远场应力；Δ σ为应力幅；Y（a）为结构几何形状函数.

在交通荷载作用下，1周时间内的裂纹扩展量为

式中：Δai为第i周的裂纹扩展量；ai和ai－1分别为第i周和第i－1周结束时的裂纹长度；Ni和Ni－1分别为第i周和第i－1周结束时的荷载循环次数.

拉索的疲劳问题属于高周疲劳，其疲劳应力幅极少超过100MPa，由此计算得到的周裂纹扩展相对速率Δ ai／ai－1＜0.01.因此式（3）可简化为

式中：Nw＝ Ni－ Ni－1.考虑到 Nw变化不大，将其作为为一个常数Nu看待.

定义

不论（Δ σ）m服从何种概率分布，由同分布中心极限定理可知，S服从正态分布，其均值ENC和方差DNC（下标NC代表单位时间的循环）可分别由下式计算得到：

式中：EΔσm和DΔσm分别为（Δ σ）m的均值和方差.

由公式（5）可以得到

式中：a0为初始裂纹长度；acr为根据钢丝断裂韧性算得的临界裂纹长度.

对于大多数公路桥梁来说，其日交通量超过千辆，交通荷载作用1周得到的有效应力循环次数超过万次，S的变异系数δS＜0.05，S的离散性对式（7）中裂纹扩展量的影响不大.因此将S放到积分号之外，并假设Nw为定值，将式（7）进一步简化为

构件在指定寿命时的可靠概率由3个相互独立的随机变量决定，分别为S，a0，和acr.

2 交通荷载分布对构件失效的影响分析

根据断裂力学原理，结构断裂的失效判据为

式中：σd为恒载应力；σlmax为交通荷载最大应力.

定义Pf（N）为构件在承受N次循环后失效的概率，则有

式中：Q（σlmax）为构件在dN次荷载循环过程中，最大交通荷载作用小于使构件断裂的临界应力的概率.

根据公式（9），（10）可以得到

式中：q（N）为最大交通荷载作用不超过N次荷载循环作用后使构件达到临界应力的概率.

由式（9）～ （11）可知

式中：a（N）为式（8）的反函数.

式（11）的解为

在工程应用中，以Nw作为时间间隔即可获得足够精确的计算结果，此时公式（13）改写为

欲使用公式（14）必须首先明确Q（σlmax）的概率分布，这可以通过Rice公式外推得到.Rice公式表达如下：

式中：v（σl）为单位时间内高斯过程上穿（或下穿）某个常数的均值；σl为交通荷载应力，将其作为一个随机过程看待；d 为σl的标准差；为 dσl／dt的标准差；μ为σl的均值.

图1为上穿和下穿概念的示意图.由图1可见x1上穿了8次，x2下穿了5次.

图1 穿越示意Fig.1 Level crossings

公式（12）中的相关参数可采用Cremona C［16］提供的方法分析计算，此处不再赘述.

定义相邻两次上穿时间间隔的平均值为回归周期TR，那么有

由随机理论，假设相邻两次上穿发生时间的间隔服从指数分布Z（1／TR），于是有

式中：QU（σl）为单位时间内σl的概率分布函数.

由公式（14）和公式（17），可以采用数值方法对交通荷载极值的影响进行分析.

3 实例分析

采用实桥WIM数据模拟交通流加载得到的某斜拉桥最不利位置两根拉索（编号分别为拉索I与拉索II）的钢丝应力谱以及Rice公式拟合参数分别见图2、图3及表1.

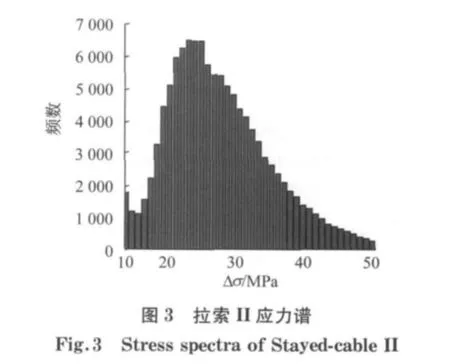
表1 Rice公式拟合参数Tab.1 Fitting parameters of Rice Equation

采用Monte－Carlo法按图2和图3中的应力谱分布模拟两根拉索中具初始缺陷钢丝的裂纹扩展失效过程.考虑到钢丝中蚀坑深度超过0.3mm时出现微裂纹的概率为50%，这里偏安全地假设初始裂纹深度为0.2mm，每根钢丝各模拟100次裂纹扩展过程.根据模拟样本计算裂纹扩展的均值和标准差见图4和图5.由图4，5可知，随着裂纹扩展，标准差由初始裂纹时的零逐渐增加，且斜率不断增大.但在构件失效前裂纹扩展量的变异系数始终很小，维持在0.01以下，这与公式（4）所采用的假设是相符合的.

图6～11分别给出了单位时间为1，4，12周3种条件下拉索I和拉索II钢丝的裂纹扩展曲线.

图6 拉索I钢丝裂纹扩展示意（单位时间为1周）Fig.6 The crack growth of Stayed－cable I wire（1week）

由图6～11可见，当以1周为单位时，按均值计算得到的结果与Monte－Carlo模拟结果较为吻合，而当以4周或12周作为单位时，由于公式（4）中的假设不再成立，Monte－Carlo模拟结果略超出均值计算结果，接近甚至超过按两倍标准差得到的计算结果.但即便在这种情况下，按均值计算的结果与Monte－Carlo法计算结果间的差异也较为有限，以图8和图11为例，按两种方法计算得到的拉索I与拉索II的钢丝达到临界裂纹长度时刻相差不超过5周.这说明应力谱随机性对构件使用寿命精度的影响有限.

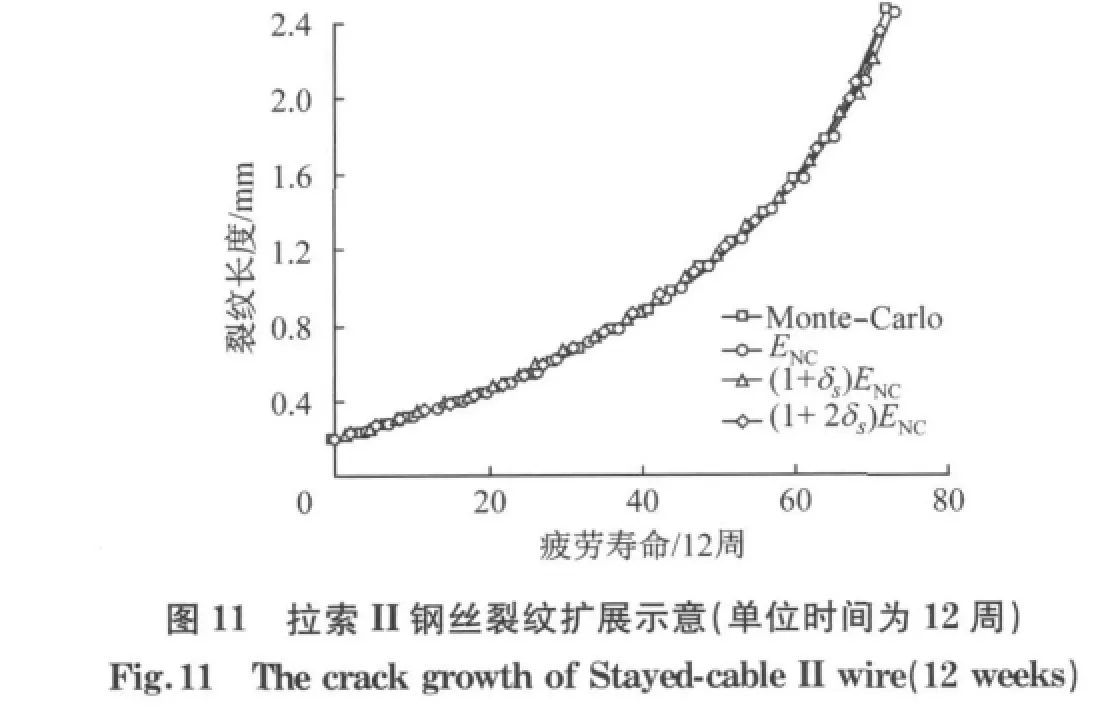
图12和图13给出了交通荷载极限应力分布对拉索临界应力随机性的影响.为了进一步展示这种影响，将对应于不同概率下的临界应力按公式（17）计算对应的重现期，列于表2中.由表2可见，要保证计算精度达到99%以上，计算临界裂纹长度所对应的临界应力至少应有15～20年的重现期.

图12 拉索I钢丝临界应力概率密度与分布Fig.12 The probability density and distribution of Stayed－cable I wire’s critical stress

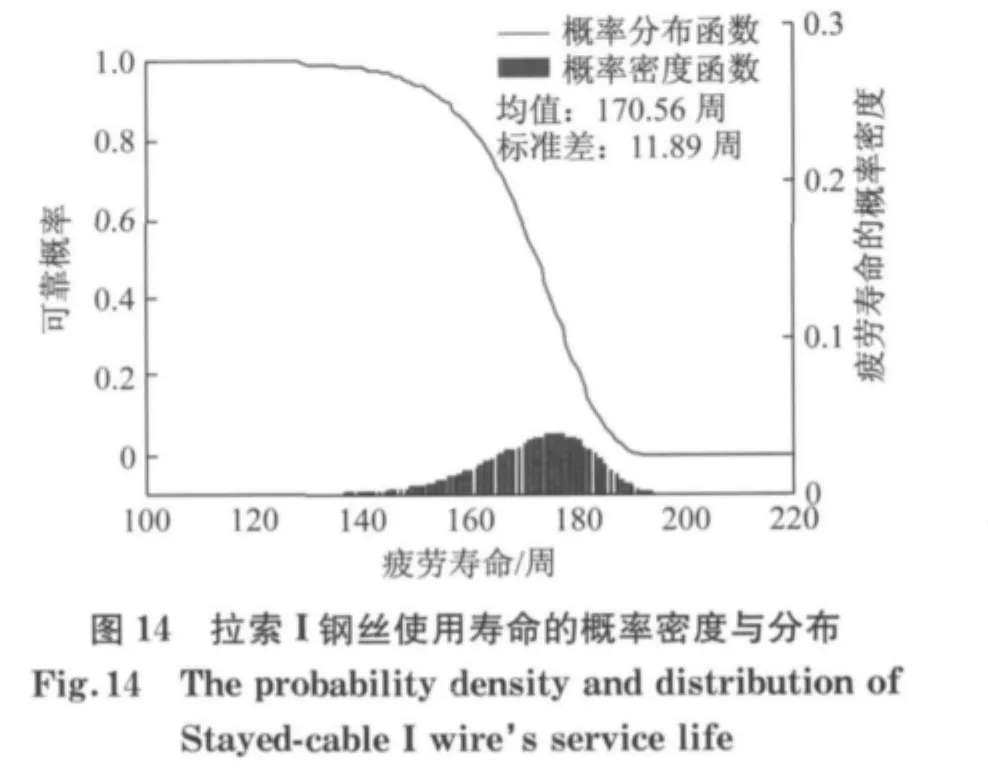
图14与图15为拉索I和拉索II的钢丝使用寿命的概率密度与分布.由于钢丝的剩余寿命与初始裂纹尺寸有关，因此图中的寿命均值意义不大.但由标准差可知，钢丝出现断裂的时间跨度主要集中在50周以内，约为1年时间.这说明疲劳寿命的计算误差可能达到1年甚至更高.

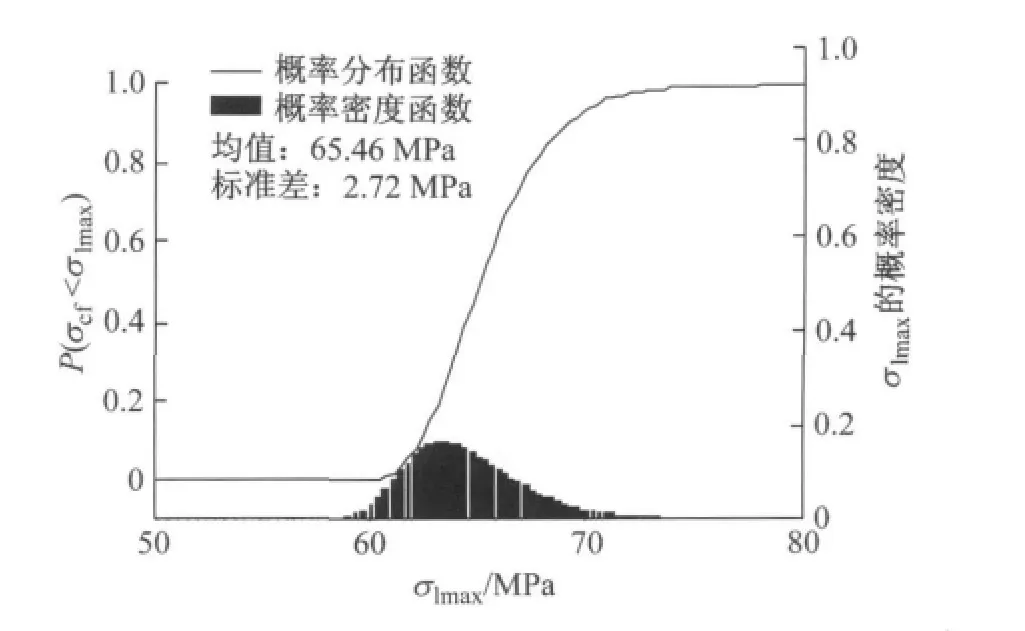
图13 拉索II钢丝临界应力概率密度与分布Fig.13 The probability density and distribution of Stayed－cable II wire’s critical stress

表2 对应保证率下应力的重现期Tab.2 The return period of critical stress corresponding to guarantee rate

4 结论

研究了疲劳应力谱及交通荷载极值对拉索钢丝疲劳寿命的影响，得到以下结论：

（1）疲劳荷载应力谱的变异性对构件疲劳寿命的影响不大.当选取较小的单位时间时，按应力谱均值计算得到的裂纹扩展寿命与实际结果较接近，两者间差异较小，但即使计算周期为12周，实际结果与简化计算结果的相差也不过5周.

（2）交通荷载效应极值的重现期对疲劳寿命的概率分布有一定的影响，使得疲劳寿命的计算误差可能达到1年.为保证其99%的可靠度，应选取对应于15年以上重现期的极限荷载作为临界荷载.

本文仅对两根实桥拉索进行了详细分析，为检验理论的正确性，需要对更多的结构进行尝试和试验检验.

［1］Fisher J W.Fatigue and fracture in steel bridges：case studies［M］.New York：Wiley，1984.

［2］Chen W Z， Wang C S，Xu L.Safety assessment and maintenance management of old steel bridge over Suzhou Creek［C］／／Second International Symposium on Steel Structures.Seoul：［s.n.］.2002：21－22.

［3］Makeev A， Nikishkov Y， Armanios E. A concept for quantifying equivalent initial flaw size distribution in fracture mechanics based life prediction models［J］.International Journal of Fatigue，2007，29（1）：141.

［4］Fjeldstad A，Wormsen A，Härkegård G.Simulation of fatigue crack growth in components with random defects［J］.Engineering Fracture Mechanics，2008，75（5）：1184.

［5］Liu Y，Mahadevan S.Probabilistic fatigue life prediction using an equivalent initial flaw size distribution［J］.International Journal of Fatigue，2009，31（3）：476.

［6］Zheng R，Ellingwood B R.Role of non－destructive evaluation in time－dependent reliability analysis［J］.Structural Safety，1998，20（4）：325.

［7］Zhang R，Mahadevan S.Fatigue reliability analysis using nondestructive inspection ［J］. Journal of Structural Engrgineering，2001，127（8）：957.

［8］Xing J，Hong Y J.A maximum likelihood method for estimates of the statistics of the crack growth behavior［J］.International Journal of Pressure Vessels and Piping，1999，76（9）：641.

［9］Lee O S，Kim D H，Park Y C.Reliability of structures by using probability and fatigue theories［J］.Journal of Mechanical Science and Technology，2008，22（4）：672.

［10］Xing J，Zhong Q P，Hong Y J.A simple log normal random process approach of the fatigue crack growth considering the distribution of initial crack size and loading condition［J］.International Journal of Pressure Vessels and Piping，1997，74（1）：7.

［11］Huang X，Hancock J W.A reliability analysis of fatigue crack growth under random loading［J］.Fatigue ＆ Fracture of Engineering Materials ＆Structures，1989，12（3）：247.

［12］Barsom J M.Fatigue crack growth under variable－amplitude loading in various bridge steels.Fatigue crack growth under spectra loads［R］.Philadelphia：American Society for Testing and Materials，1976.

［13］Paris P C.The fracture mechanics approach to fatigue.Fatigue—an interdisciplinary approach［M］.New York：Syracuse University Press，1964.

［14］Foreman R G，Keart V E，Engle R M.Numerical analysis of crack propagation in cycle－loaded structures［J］.Journal Basic Engineering，1967，89：459.

［15］Weertman J.Rate of growth of fatigue cracks calculated from the theory of infinitesimal dislocations distributed on a plane［J］.International Journal of Fracture Mechanics，1966，2：460.

［16］Cremona C.Optimal extrapolation of traffic load effects［J］.Structural Safety，2001，23（1）：31.