一种基于复数变量求偏导的随机有限元可靠度法

靳 慧

（1.东南大学 江苏省工程力学分析重点实验室，江苏 南京 210096；2.重庆交通大学 桥梁结构工程重点实验室，重庆 400074）

随机有限元方法（SFEM）是计算随机力学的一个重要分支，是随机结构分析的有力工具.SFEM能够处理工程中的结构随机问题，计算结构随机响应量的统计特征.近几十年来，国内外学者对随机有限元法进行了大量深入的研究［1－3］，提出了众多的求解方法，如Monte－Carlo随机有限元法，Taylor展开随机有限元法（TSFEM），摄动随机有限元法（PSFEM），Neumann展开随机有限元法（NSFEM）等，成功地解决了大量工程中的随机结构分析问题.

除了Monte－Carlo随机有限元法外，其他随机有限元法都是在传统的确定性有限元列式的基础上，进行推导演化，得出迭代式，以计算响应量对各随机变量的各阶偏导数，然后根据这些偏导数和泰勒级数展式计算出响应量的各阶统计特性.可见，偏导数的计算是随机有限元法的核心.

另外，随机有限元法的重要用途是和可靠度理论相结合进行结构可靠性分析，称为随机有限元可靠度法（SFEMR）.在可靠度计算方法中，需要计算功能函数对各个随机变量的偏导数，而这种偏导数的计算往往又通过功能函数的表达式转化为结构随机响应量的偏导数计算.所以，响应量的偏导数计算直接影响SFEM和SFEMR的计算精度和效率.本文将复数变量求偏导法引入到SFEM和SFEMR中，提出一种快速、精确的求偏导方法，可大大简化SFEM和SFEMR计算过程，提高计算效率.

1 随机有限元法

一阶摄动法和一阶Taylor展开法的计算过程较为简单，适用于随机变量变异系数较小的情况.

1.1 摄动随机有限元法

摄动随机有限元法假设结构的某一个参数Y是随机扰动的，其扰动量可以用一个随机小参数α来表示［2］，Y＝（1＋α）为Y的均值.

有限元控制方程为

式中：K为总刚矩阵；v为位移列阵；F为等效节点载荷列阵.

当有限元离散网格确定以后，将刚度矩阵、载荷列阵和位移列阵在随机向量α（αi，αj，…）的均值处Taylor级数展开，并略去二阶以上项，有

式中：K0，F0，v0分别表示刚度矩阵、载荷列阵和位移列阵的均值矩阵，它们是确定性量；下标i表示对αi求偏导数.将式（2），（3），（4）代入控制方程（1），运用中心摄动方法可以得到如下的递归方程组：

由式（5）可以得出位移的均值E和协方差Cov

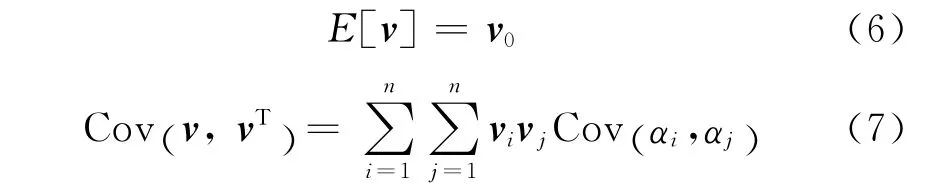
1.2 Taylor展开随机有限元法

该法的基本思路是将有限元格式中的控制变量在随机变量均值点处进行Taylor展开，经适当数学处理得出所需计算式［3］.

有限元控制方程为Kv＝F，应力向量σ由下式计算：

式中：D为弹性矩阵；B为应变矩阵.

X＝ （X1，X2，…，Xn）为表示结构材料、几何、载荷等随机性质的随机向量.将应力σ在均值点处一阶Taylor展开，并在两边同时取均值，可得

式中：D0，B0分别表示弹性矩阵和应变矩阵的均值，而

以上两式与常规确定性有限元的计算完全相同.应力的方差Var可由下式计算：

1.3 随机有限元法中的偏导数计算

可以看出，SFEM中结构位移和应力的均值计算等同于确定性有限元；方差计算式（7）和（11）的关键在于求解位移和应力对随机变量的偏导.对于线弹性结构，直接对有限元方程求偏导可得

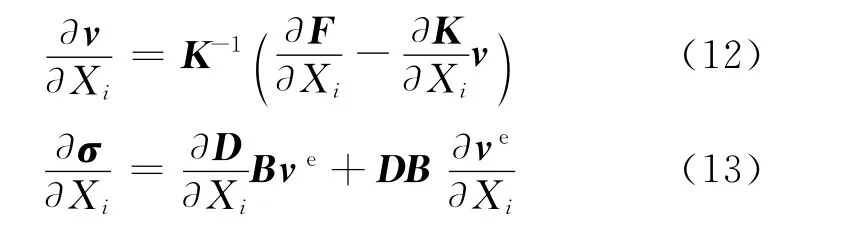
式中：ve表示单元位移阵列.

这种直接求偏导法可得到解析解，但需要对有限元矩阵进行求导、求逆等多次运算，过程复杂.

另外一种简便求解偏导数的方法是有限差分法，函数f（x）对变量x的偏导数由下式计算

式中：h为微小扰动量.有限差分法虽然避免了对矩阵进行计算，只需求解函数值f，但精度差，且对扰动量h的依赖性很强.

复数变量法是一种精度和效率都极高的偏导数求解方法，本文将此法运用到SFEM和SFEMR中.

2 复数变量求导法

复数变量求导法由Lyness和Moler于1967年提出［4］，Vatsa V N用于解 Navier－Stokes流动方程的灵敏度偏导［5］，Daniel Contreras Mundstock等用在二维弹性的灵敏度估算问题中［6］，Gao X W用在非线性边界元的求解中［7］.

将函数f（x）的变量x替换为复数变量x＋i h，h为微小扰动量，f（x＋i h）可以展开为Taylor级数展式：

一阶偏导数可以表示为

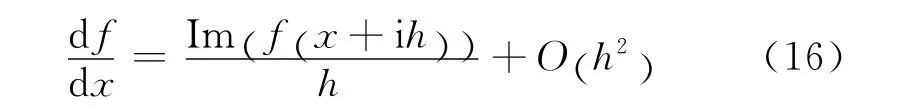
Im表示复数的虚部，忽略高阶微小量O（h2），则有

式（17）即为复数变量法求一阶导数的计算式，和其他方法相比，复数变量求导法有以下几个特点：

（1）精度高.由式（17）可见，在复数空间进行计算，一次导数计算时只需求一个复数函数值f（x＋i h），不存在多个函数之间的运算误差，算例表明具有很高的精度.

（2）扰动量h可取微小值.在复数空间进行计算，高阶微小量O（h2）随微小扰动量h的减小而高次减小，h取微小值时，偏导计算精度高.有限差分法需要计算两个函数值f（x＋h）和f（x－h）的差，当h取微小值，这两个函数值在一个数量级时，相减计算可能导致误差.而复数变量求一次导数计算时只需求一个函数值，对扰动量h的依赖性低.

（3）应用简单方便.

图1为平面桁架结构，载荷P1＝35500N，P2＝36100N，弹性模量E＝2.0×1011Pa，杆件横截面积A＝0.00320m2.求杆件最大应力值σmax对随机变量A，P1的偏导数.有限元程序采用平面杆单元编制，由直接求偏导法求得解析解.

列出一段复数变量求偏导的Matlab程序，这段程序是算例1中计算桁架结构中的最大杆应力响应量Ymax对杆件横截面积A的偏导数∂Ymax／∂A.

A＝0.00320m2；%A为桁架中所有杆件的横截面积

P1＝35500N；%P1，P2为载荷值

P2＝36100N；

E＝2×1011Pa；%E为弹性模量

h＝1×10－6；%h为扰动量

A＝A＋hi；%设置A为复数变量

FEM程序；%有限元程序计算Ymax

∂Ymax／∂A＝Im（Ymax）／h；%计算∂Ymax／∂A

可以看出，复数变量法只需在FEM程序前通过语句A＝A＋hi设置A为复数变量，在FEM程序后只用一条语句∂Ymax／∂A＝Im（Ymax）／h取出Ymax的虚部，并根据式（17）计算偏导，其余的程序完全与实数空间的FEM程序相同，计算所耗机时与普通有限元程序运行机时并无差异.与直接求偏导法相比，省去了矩阵的求逆和求导等运算，计算过程大大简化，并且程序编制极其简单，只需对实数空间的FEM程序进行简单的设置即可.

复数变量法和有限差分法的计算结果见表1.

图1 平面桁架结构Fig.1 Plane truss structure

表1 偏导数计算结果Tab.1 Results of derivative

由表1可见，计算∂σmax／∂A 时，只有h＝1.0×10－8时，有限差分法计算结果与解析解比较接近，而当h取其他值时，都会产生较大的误差；复数变量法在h取值足够小，小于1.0×10－6时，都会得出很精确的结果.∂σmax／∂P1的计算也有类似的结论.

3 随机有限元可靠度法

随机有限元法的重要用途是和可靠度理论相结合进行结构可靠性分析，目前使用最多的是随机有限元一次二阶矩法.

3.1 改进的一次二阶矩法

设结构构件功能函数为［8］

式中：Xi（i＝1，2，…，n）为统计独立正态随机变量.

将功能函数在设计验算点x＊（，…）作Taylor级数展开，仅保留线性项，有

可得Z的均值与方差为

式中：uXi表示Xi的均值；σXi表示Xi的方差.

可靠度系数β为

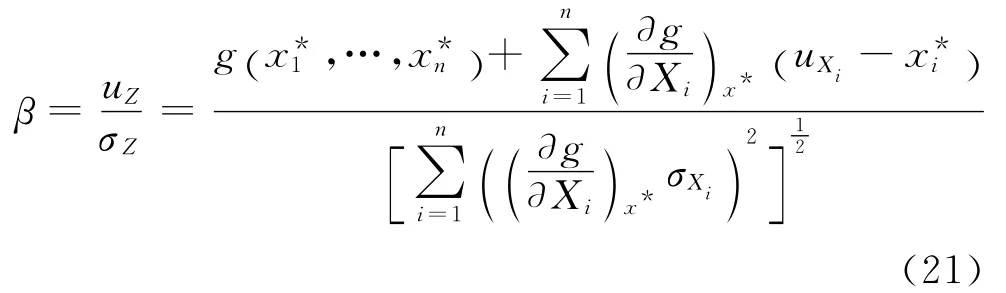
设计验算点坐标为

β的求取只能采用迭代法，计算步骤为：

（2）求cosθXi，采用式（23）.

（3）求β，采用式（21）.

3.2 随机有限元一次二阶矩法

利用式（21），（23）计算可靠度指标β时，要用到功能函数的值g （，…）和功能函数对随机变量的偏导数值.功能函数g往往是结构响应量s（位移，应力等）的函数g＝f（s），所以求g的值和偏导数转化为求s的值和偏导数，即

响应量s的值和偏导可通过SFEM法求出，也就是将SFEM嵌入到一次二阶矩的迭代中，形成随机有限元一次二阶矩法，其迭代步骤为：

（2）由SFEM 求s和∂s／∂X.

（3）求g和∂g／∂X，采用式（24），（25）.

（5）求β，采用式（21）.

每迭代一次求解β，就要解一次随机有限元，求解的关键是计算∂s／∂X，可采用复数偏导法.

4 复数变量求偏导SFEMR法

由式（15）所示的f（x＋i h）的Taylor级数展式可得

忽略高阶微小量O（h2），则有

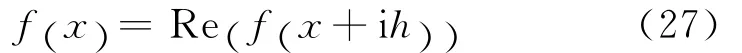
对于FEM，在复数空间进行运算，可取复数计算结果的实部作为响应量的值，取复数计算结果的虚部计算响应量的偏导，无需再在实数空间进行计算.

在3.2节的随机有限元一次二阶矩法的迭代格式中，用复数空间的FEM取代SFEM，迭代格式为：

（2）进行复数空间FEM计算.取复数响应量的实部作为s的值，采用式（27）；取复数响应量的虚部求解∂s／∂X 的值，采用式（17）.

（3）求g和∂g／∂X，采用式（24），（25）.

（5）求β，采用式（21）.

和随机有限元一次二阶矩法相比，本节方法用复数空间的FEM计算代替了SFEM计算，其程序的编制只需普通的FEM程序，无需再编制SFEM程序，运算过程大大简化.

以算例1中的桁架结构为例，设A，P1，P2分别为复数变量且随机扰动，根据式（27）计算得到的最大杆件应力值σmax和实数空间的有限元结果比较见表2.

设杆件强度为R＝8.0×107MPa，A，P1，P2的变异系数为0.2，复数扰动量取h＝10－30，计算危险点的强度可靠度.功能函数为g＝R－σmax.根据第4节的迭代步骤计算可靠度系数β和验算点的值，迭代过程如表3所示.

表2表明，在复数空间运用式（27）计算有限元响应量的值具有很高的精度.表3表明，在求解β的迭代过程中，只需在复数空间进行普通FEM计算，过程大大简化.

表2 最大杆件应力值σmax计算结果Tab.2 Results of the max stressσmaxin plane truss

表3 求解β迭代过程Tab.3 Iterative process forβ

5 结论

复数变量求导法效率高，精度高，应用简单方便，只需在复数空间进行有限元计算，便可求出响应量的偏导数，用在随机有限元中，可求得响应量的方差.与直接求偏导法相比，省去了矩阵的求逆和求导等大量运算，计算过程大大简化.

在随机有限元一次二阶矩的迭代格式中，取复数空间有限元的计算结果的实部作为响应量的值，虚部用来求解响应量的偏导.这样在求β的迭代过程中，只需进行复数空间的有限元计算，无需再在实数空间进行计算.

随机有限元法可解决工程中的随机结构分析问题，是随机结构分析的有力工具.但其实现需要专门的程序，目前还没有商业软件可供利用.本文提出的复数变量法大大简化了SFEM和SFEMR的实现过程，为工程应用提供了一种现实可行的途径.

［1］王建军，于长波，李其汉.工程中的随机有限元方法［J］.应用力学学报，2009，26（2）：297.WANG Jianjun，YU Changbo，LI Qihan.Stochastic finite element methods in engineering［J］.Chinese Journal of Applied Mechanics，2009，26（2）：297.

［2］陈虬，刘先斌.随机有限元法及其工程应用［M］.成都：西南交通大学出版社，1993.CHEN Qiu，LIU Xianbin.Stochastic finite element methods and its application［M］.Chengdu：Press of Southwest Jiaotong University，1993.

［3］刘宁.可靠度随机有限元法及其工程应用［M］.北京：水利水电出版社，2001.LIU Ning.Reliability stochastic finite element methods and its application to engineering［M］.China Water Power Press，2001.

［4］Lyness J N，Moler C B.Numerical differentiation of analytic functions［J］.SIAM Journal on Numerical Analysis，1967（4）：202.

［5］Vatsa V N.Computation of sensitivity derivatives of Navier－Stokes equations using complex variables［J］.Advances in Engineering Software，2000，31：655.

［6］Daniel Contreras Mundstock，Rogério JoséMarczak.Boundary element sensitivity evaluation for elasticity problems using complex variable method［J］.Struct Multidisc Optim，2009，38：423.

［7］Gao X W，Liu D D，Chen P C.Internal stresses in inelastic BEM using complex－variable differentiation ［J］. Computational Mechanics，2002，28：40.

［8］张新培.建筑结构可靠度分析与设计［M］.北京：科学出版社，2001.ZHANG Xinpei.Reliability analysis and design of building strictures［M］.Beijing：Science Press，2001.