单框架控制力矩陀螺转子动不平衡对遥感卫星成像的影响
杨秀彬 ,常 琳,金 光
(1.中国科学院 长春光学精密机械与物理研究所,吉林 长春130033;2.中国科学院 研究生院,北京100039)
1 引 言
随着航天事业的发展,人们对对地观测小卫星的拍照精度要求越来越高。对地拍照高分辨率成像意味着相对较小的视场孔径角,而要实现对敏感区域大范围拍照,就要求小卫星具有快速的机动能力,即要求卫星姿态控制系统能够提供足够大的控制力矩。单框架控制力矩陀螺( Single Gimbal Control Moment Gyro,SGCMG) 既具有力矩放大能力,能够提供更大的控制力矩,又能精确连续地输出力矩,并且不消耗燃料,不会对光学设备和飞行环境造成污染[1-4],因此,控制力矩陀螺以能提供较大的角动量能力成为姿态控制执行机构的首选配置。然而,控制力矩陀螺转子质量分布的微小不平衡会在高速旋转过程中对卫星产生方向和大小均随时间而改变的扰动,引起卫星的振动响应、姿态扰动响应和颤振响应,进而影响遥感卫星对地成像的质量。
目前,关于控制力矩陀螺的动不平衡干扰力矩对高分辨力相机成像影响的分析研究未见报道,因此,研究SGCMG 转子动不平衡对卫星成像的影响可以为SGCMG 在卫星相机上的应用提供论证,进而对SGCMG 的减震措施提供依据。本文对SGCMG 转子高速旋转时动不平衡导致的TDI CCD 成像质量的下降进行了理论分析与模拟仿真。
2 陀螺转子的动不平衡分析
根据SGCMG 工作原理,SGCMG 转子在高速旋转工作过程中转速是恒定的,SGCMG 通过沿框架轴的进动来产生陀螺控制力矩,以抵消外部扰动力矩或按要求进行机动。高速旋转的陀螺转子能够产生动态不平衡力矩。陀螺转子的动态不平衡表示由于陀螺转子质量分布不均致使其惯量积不为零,此时同样可将陀螺转子质量分为两部分,其一为严格对称部分,其惯量积为零;其二为两个沿旋转轴方向距离为2h的点质量md,它们的连线同转轴共面,且距离转轴均为rd,如图1 所示。
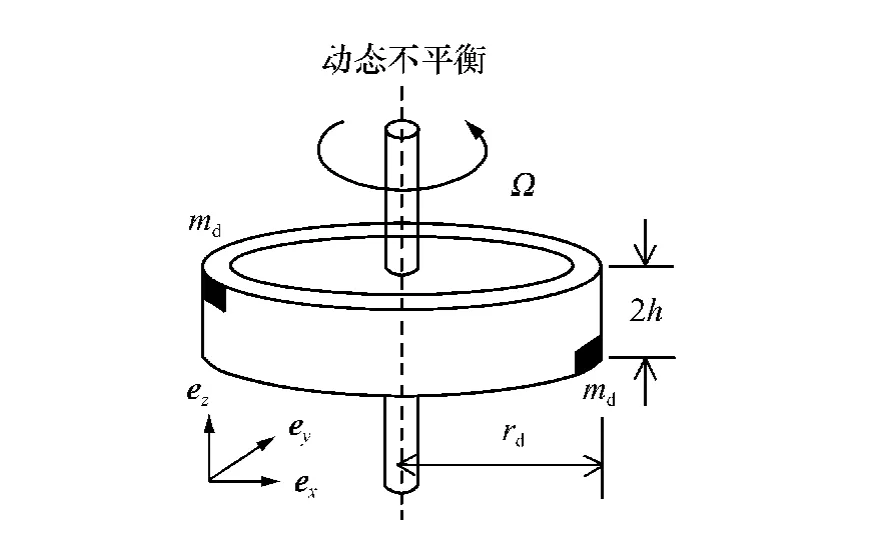
图1 陀螺转子动态不平衡示意图Fig.1 Diagram of dynamic imbalance for gyro rotor
当陀螺转子旋转时,两个点质量md旋转产生的力矩[5]为:
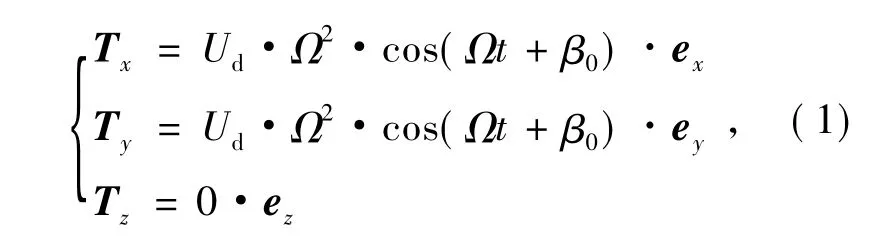
式中:Ω 为飞轮旋转角速度,β0为初始相位,Ud=2mdrdh,假设β0=0。
3 动不平衡力矩引起高分辨力小卫星的颤振响应
由于式( 1) 中SGCMG 转子动不平衡干扰力矩的计算仅在陀螺转子部件上,因此计算它对卫星的颤振影响需要建立相应坐标系,将其转换至星体坐标系,在星体坐标系下,利用星体姿态动力学方程,计算出陀螺转子动不平衡力矩引起的卫星的颤振角位移和颤振角速度,相应的坐标变换如图2 所示,建立的坐标系包括:
陀螺转子坐标系o-xryrzr,框架坐标系o-xgygzg,陀螺基座坐标系o-xbybzb,卫星本体坐标系o-xsyszs,卫星相机坐标系o-xcyczc。
其中,γi为转子转角,ζi为框架转角,Ω 为陀螺转子绕旋转轴旋转的角速度,β 是每个陀螺框架轴与卫星本体坐标系o-xsyszs的zs轴夹角,αi是框架轴在卫星本体坐标平面xsys的投影与xs轴的夹角,i=1,2,…N,N是控制力矩陀螺的总个数。
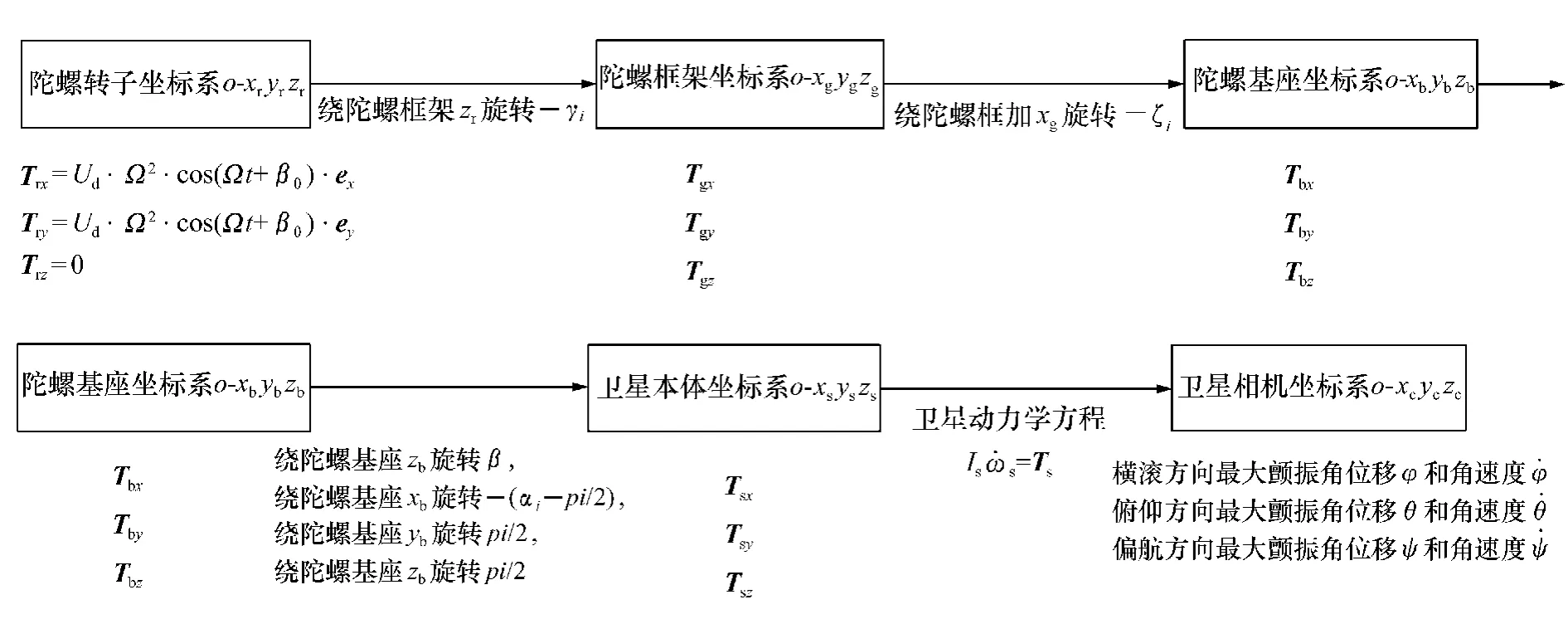
图2 陀螺转子坐标系到星体坐标系的转换关系Fig.2 Transformation system from gyro coordinate to satellite coordinate
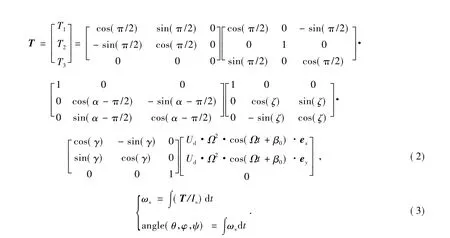
4 颤振对成像的影响分析
高分辨力小卫星对地侦察成像时,采用TDI CCD 推扫摄像的航天光学遥感相机,为满足高分辨力成像要求,须在轨实时计算和实时精确补偿地物和其它姿态轨道参数在像面上产生的像移速度矢,在影响像移速度矢诸参数中,姿态角位移和姿态角速度最为重要。下面利用高精度像移补偿模型构建颤振角位移和角速度在相机焦平面上影响成像的像元失配量[6-11],进而利用TDI CCD 相机像点与物点对应的成像模型分析SGCMG 动不平衡对高分辨力小卫星成像的影响,图3 是像移补偿模型中物点与像点对应的成像坐标变化。
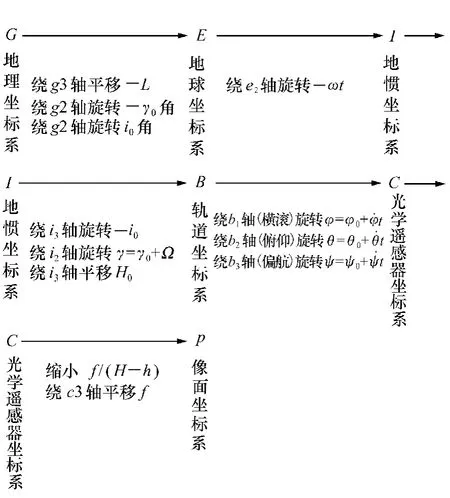
图3 地物至像面的成像坐标变换Fig.3 Coordinate transformations from ground to image plane
其中:f为相机镜头焦距;R为相对于地心的地球半径;h为被摄景物处的地物地形高度;Ω 为飞船轨道运动相对地心的角速率;i0为轨道倾角;H为被摄景物处飞船的轨道高度;γ0为在摄影时刻,飞船在轨道平面到降交点或升交点之间所对应的中心角;ψ·,θ·,φ·分别为飞船坐标系相对于轨道坐标系的偏航、俯仰和横滚姿态角速度;ψ0,θ0,φ0分别为飞船坐标系相对于轨道坐标系在摄影时刻的偏航、俯仰和横滚姿态角。
5 实验仿真
这里仿真分析SGCMG 转子动不平衡干扰力矩引起的星体颤振角位移和角速度对TDI CCD相机成像的影响,具体流程如图4 所示。采用的SGCMG 为金字塔构型,如图5 所示。仿真计算中,取动不平衡因子Ud=5 gcm2,转子旋转速度分别为3 000 和6 000 r/min,则转子角速度Ω3000=50 ×2π rad/s,Ω6000=100 ×2π rad/s,金字塔构型SGCMG 框架轴与zb轴夹角为30°,每个陀螺框架轴与卫星本体坐标系o-xsyszs的zs轴夹角分别为45,135,225,315°,星体转动惯量为Ib。计算得到的SGCMG 转子动不平衡引起的星体颤振角位移和角速度如图6 ~9 所示。将星体颤振角位移和角速度代入TDI CCD 相机像点与物点对应模型的仿真系统进行试验仿真[3],模拟仿真SGCMG转子旋转速度在3 000 和6 000 r/min 时TDI CCD的成像,相应结果见表1。成像如图10 ~图11 所示,相应的成像调制函数MTF 和图像的互相关相似性测度ρ 见表2。
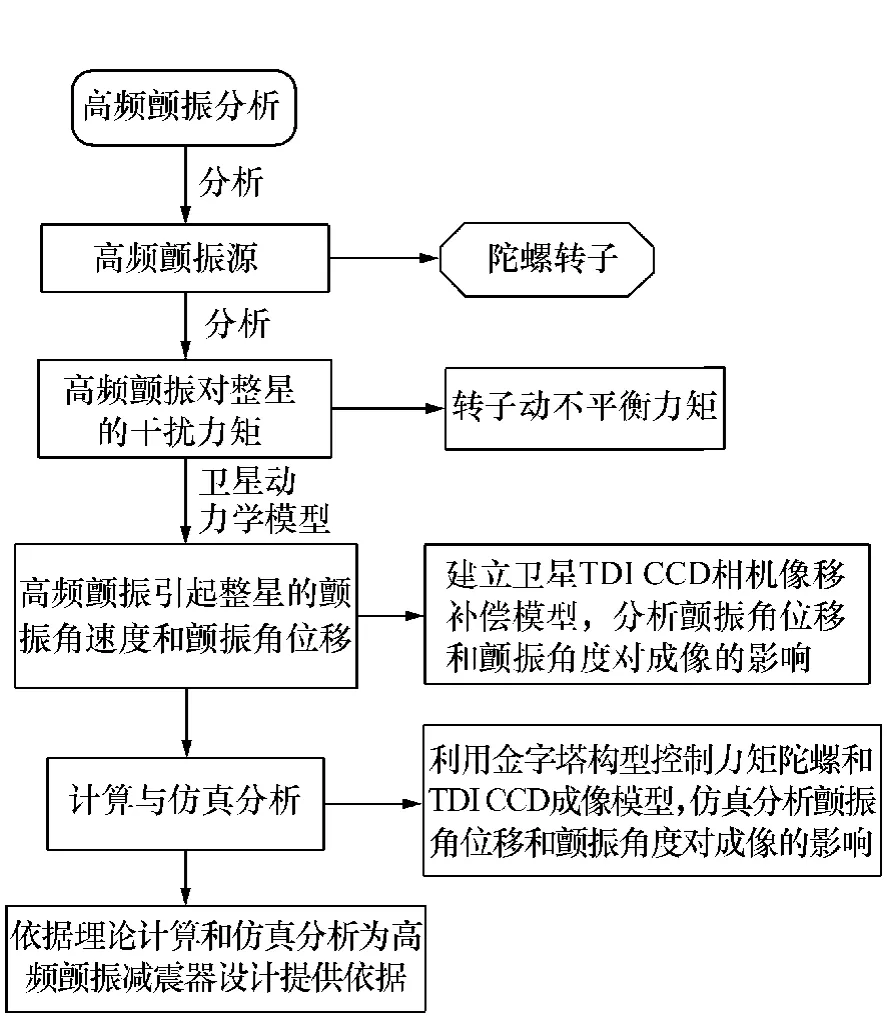
图4 颤振对成像影响分析流程图Fig.4 Flow chart of influence of vibration on imaging
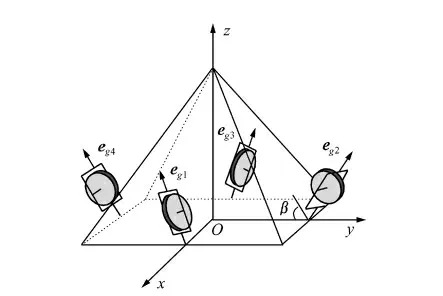
图5 金字塔构型SGCMG 系统Fig.5 SGCMG system with pyramid configuration
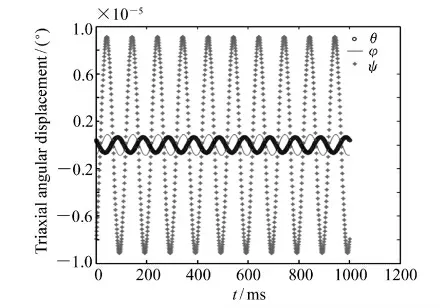
图6 SGCMG 转子转速为3 000 r/min 时的颤振角位移Fig.6 Vibration angular displacement of SGCMG rotor at rotating speed of 3 000 r/min

图7 SGCMG 转子转速为3 000 r/min 时的颤振角速度Fig.7 Vibration angular velocity of SGCMG rotor at rotating speed of 3 000 r/min
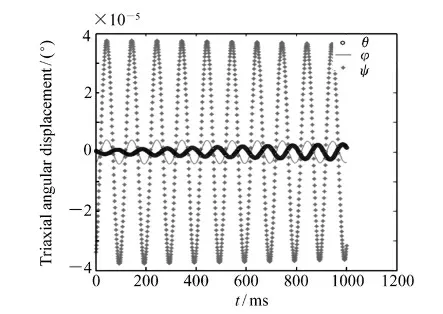
图8 SGCMG 转子转速为6 000 r/min 时的颤振角位移Fig.8 Vibration angular displacement of SGCMG rotor at rotating speed of 6 000 r/min
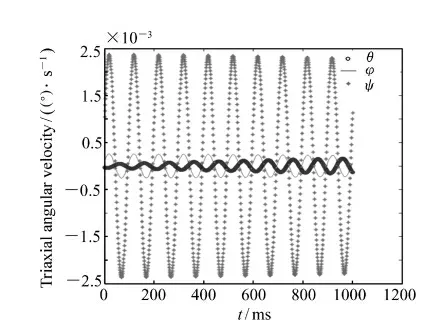
图9 SGCMG 转子转速为6 000 r/min 时的颤振角速度Fig.9 Vibration angular velocity of SGCMG rotor at rotating speed of 6 000 r/min

图10 SGCMG 转子转速为3 000 r/min 时的仿真成像Fig.10 Simulation imaging of SGCMG rotor at rotating speed of 3 000 r/min

图11 SGCMG 转子转速为6 000 r/min 时的仿真成像Fig.11 Simulation imaging of SGCMG rotor at rotating speed of 6 000 r/min

表1 与转子旋转速度对应的三轴方向的最大颤振角位移和最大颤振角速度(输入条件:I0 =5 gcm2)Table 1 The maximum vibration angular displacements and angular velocities for three axises corresponding to the rotation speed on condition of I0 =5 gcm2

图12 假设的景物图像Fig.12 Hypothetical scenery picture
6 颤振角位移和角速度引起的像移及传递函数
由于TDI CCD 成像过程中有纵向和横向像移,传递函数分为纵向传递函数与横向传递函数。纵向像移由不可补偿像移和可补偿像移组成。
不可补偿像移是TDI CCD 像元在采集光信号过程中产生的像移。CCD 线阵在推扫成像过程相当于狭缝扫描成像,对应的像移量即为CCD的像元宽度。这种情况下的像移是不能补偿的,由此而产生的MTF 为:
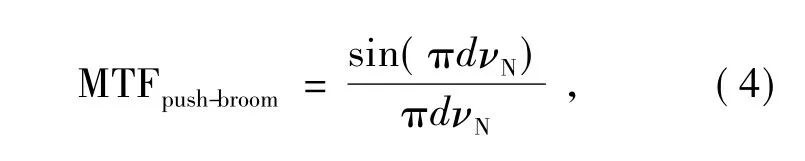
式中:d为像元的宽度,νN为Nyquist 频率。
可补偿像移是由于相机本身的偏流角误差和焦距误差卫星飞行高度、飞行速度、姿态角速率变化、TDI CCD 行转移速率的控制误差以及卫星平台侧视畸变等因素导致的TDI CCD 行转移时间和地面目标在TDI CCD 靶面上像的移动速度不匹配造成的像移量,对应MTF 匹配残余误差。
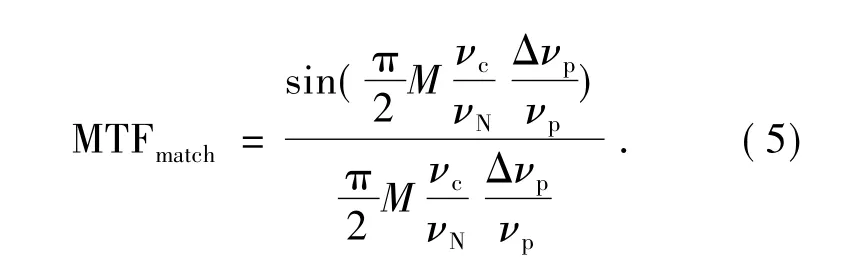
为对比图像需要,式中: 取TDI CCD 级次为M,特征频率νc=νp,Δνp/νp为TDI CCD 像移匹配的速度残余误差,MTFmatch为沿推扫方向的MTF,纵向像移产生的在扫描方向上的MTF 为:
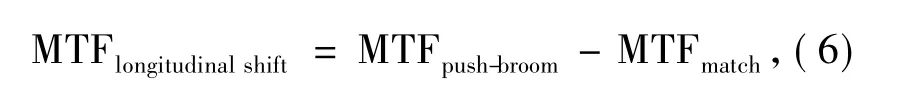
横向像移产生在垂直于TDI CCD 推扫方向上,横向匹配的残余像移产生的MTF 值为:
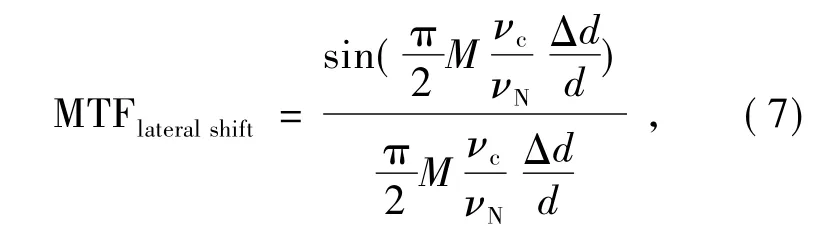
式中,Δd/d为由于偏流角匹配误差产生的横向匹配的残余误差。
根据表2 分析得出,SGCMG 作为卫星姿态执行机构,高速旋转的陀螺转子产生的干扰力矩会引起星体的颤振角位移和颤振角速度。其中,转子旋转速度在6 000 r/min,偏航方向最大颤振角速度达到0.002 5 ( °) /s,从而引起组合矢量方向上的合成速度和TDI CCD 时间延迟转移速率不匹配,图像的纵向与横向的传递函数变小,尤其是横向传递函数迅速下降。图像的互相关相似性测度不断减小,成像清晰度变差。

表2 SGCMG 转子动不平衡对TDI CCD 相机成像的影响Table 2 Effect of dynamic imbalance for SGCMG rotor on TDI CCD camera imaging
7 结果与讨论
对仿真所得图6 ~11 和表1 ~2 所列数据分析如下:( 1) SGCMG 作为卫星姿态执行机构,陀螺转子在高速旋转过程会对星体产生颤振角位移和角速度,陀螺转子速度越快,对星体产生的颤振角位移和角速度越大; ( 2) 由于星体产生的高频颤振角位移和角速度的影响,TDI CCD 扫描图像存在与成像推扫方向垂直的横向像移速度,使各级像点收集的电荷混淆,图像发生混淆现象,另外存在推扫成像方向上的像移速度,引起TDI CCD推扫方向的电荷转移速度与实际像移速度不同步;( 3) 在其它参数一定的情况下,随着高频颤振角速度和角位移的增加,图像的互相关相似性测度与传递函数急速下降,在陀螺转子旋转速度为3 000 r/min时,MTFlongitudinalshift为0.639,MTFlateralshift为0.997,图像互相关相似性测度为0.996 1,在陀螺转子旋转速度为6 000 r/min 时,MTFlongitudinalshift为0.638 5,MTFlateralshift为0.928 3,图像互相关相似性测度为0.974 8。结果表明:SGCMG 作为卫星姿态执行机构,陀螺转子在高速旋转过程中引起的星体颤振角位移和角速度对TDICCD 相机的成像质量影响较为严重。
8 结 论
本文根据金字塔构型的SGCMG 工作原理,分析了SGCMG 转子动不平衡干扰力矩引起的星体颤振角位移和颤振角速度对TDI CCD 相机成像的影响。高分辨力相机对成像失配要求严格,所以要对颤振进行分析,从而对控制力矩陀螺进行减振措施,这为SGCMG 在卫星载荷上的应用提供了论证,进而对SGCMG 的减振措施提供了依据。
[1] LAPPAS V J. A control moment gyro( SGCMG) based attitude control system( ACS) for agile small satellites[D]. Surrey:University of Surrey,2002.
[2] WIE B. Singularity escape/avoidance steering logic for control moment gyro systems[J].J Guidance,Control,and Dynamics,2005,28(5) :948-956.
[3] 胡君,王栋,孙天宇.现代航天光学成像遥感器的应用与发展[J].中国光学与应用光学,2010,3(6) :519-533.HU J,WANG D,SUN T Y,et al.. Application and development of recent space optical imaging remote sensors[J].Chinese J. Opt. Appl. Opt.,2010,3(6) :519-533.( in Chinese)
[4] 杨秀彬.太阳同步天回归轨道的高分相机像移补偿研究[D].北京:中国科学院研究生院,2011.YANG X B. Research on sun-synchronous and day recursive orbit high resolution camera image motion compensation[D]. Beijing:Graduate University of Chinese Academy of Sciences,2011.( in Chinese)
[5] 李连军,戴金海.反作用轮系统内干扰建模与仿真分析[J].系统仿真学报,2005,17(8) :1855-1863.LI L J,DAI J H. Inner disturbance modeling and simulation analysis of reaction wheel system[J].J. System Simulation,2005,17(8) :1855-1863.( in Chinese)
[6] WANG J Q,YU P,YAN CH X,et al. Space optical remote sensor image motionvelocity vector computational modeling,error budget and synthesis[J].Chin. Optics Lett.,2005,3(7) :414-417.
[7] 杨秀彬,金光,张刘.卫星后摆补偿地速研究及成像仿真分析[J].宇航学报,2010,31(3) :912-917.YANG X B,JIN G,ZANG L. Satellite swaying to compensate earth speed research and imaging simulation analysis[J].J.Astronautics,2010,31(3) :912-917.( in Chinese)
[8] 郑耿峰,张柯,韩双丽,等.空间TDICCD 相机动态成像地面检测系统的设计[J].光学 精密工程,2010,18(3) :623-629.ZHENG G F,ZHANG K,HAN S J,et al.. Design of test system for motion images of space TDICCD cameras[J].Opt.Precision Eng.,2010,18(3) :623-629.( in Chinese)
[9] 袁修孝,曹金山,姚娜.顾及扫描侧视角变化的高分辨率卫星遥感影像严格几何模型[J].测绘学报,2009,38(2) :120-124.YUAN X X,CAO J S,YAO N. A rigorous geometric model considering the variety of side watch angle for high resolution satellite imagery[J].Acta Geodaeticaet Carto graphica Sinica,2009,38(2) :120-124.( in Chinese)
[10] 窦闻,陈云浩,何辉明.光学遥感影像像素级融合的理论框架[J].测绘学报,2009,38(2) :131-137.DOU W,CHEN Y H,HE H M. Theoretical framework of optical remotely sensed image fusion[J].Acta Geodaeticaet Carto graphica Sinica,2009,38(2) :131-137.( in Chinese)
[11] 杨秀彬,张刘,金光.偏流角误差对TDI CCD 相机成像的影响与仿真[J].光电工程,2008,35(11) :45-50.YANG X B,ZHANG L,JIN G. Effect and simulate of the deviant angle erroron TDI CCD cameras image[J].Opo-Electronic Eng.,2008,35(11) :45-50.( in Chinese)

