菲索式合成孔径望远镜光学系统设计

段相永，乔彦峰 ，王永伟，孙玉铭

(1.中国科学院 长春光学机密机械与物理研究所，吉林 长春130033;2.中国科学院 研究生院，北京100039; 3.空军驻长春地区军事代表室，吉林 长春130033;4.二炮驻锦州地区专装军事代表室，辽宁 锦州121000)

1 引 言

随着对空间目标分辨率要求的提高，望远镜光学系统的孔径也越来越大，但是孔径的增大受材料、工艺水平、成本等相关因素限制［1-3］，因此，探索大口径光学系统的新原理、新技术、新途径显得尤为重要。合成孔径干涉阵列成像技术为克服大口径光学系统制造难问题提供了一种解决途径。合成孔径干涉阵列成像系统按照阵列结构特点分为迈克尔逊干涉和菲索干涉两种。长基线的迈克尔逊式干涉阵列望远镜是各个子孔径的出射光被反射到光束组合器( 半反半透镜) 合为一束光，再进入图像采集器，经过一段时间的曝光出现干涉条纹( 光瞳平面光束组合) 。菲索式干涉阵列望远镜是各个子孔径的出射光按照特定的排列方式入射到光束组合器( 有光焦度的成像系统)入瞳面并在光束组合器像面干涉成像( 像面光束组合)［4-6］。与长基线的迈克尔逊干涉系统比较，采用菲索干涉系统的望远镜结构更加紧凑，能够对空间频率u-v 全覆盖，实现瞬时成像，因此适用于对快速移动目标的高分辨率成像［4］。

国外菲索式合成孔径干涉阵列成像技术的研究工作起步较早，并取得了一定的研究成果。最早的菲索式合成孔径干涉望远镜是1978 年美国亚利桑那大学建造的多镜面望远镜( Multiple Mirror Telescope，MMT) 。它由6 个口径为1.8 m 的子望远镜组成，等效口径为4.45 m，视场为30″，但是该系统只有很小一部分视场能够被定相，同时需要一个有经验的操作人员进行人工调整。另一个著名的菲索式合成孔径干涉望远镜是安装在Graham山上的大型双目望远镜( Large Binocular Telescope，LBT) 。它由两个口径为8.4 m 并排安装的子望远镜组成，视场为1'，最高成像分辨率等价于22.65 m 口径光学系统衍射极限分辨率。90 年代后期，法国Dame 等人提出的太阳物理成像干涉仪( SOLARNET) ，由3 个口径为350 mm的子望远镜组成，视场为40″，基线长为1 m。2002 年麻省理工学院研制的自适应侦察Golay-3光学卫星地面样机( ARGOS) 由3 个口径为210 mm的子望远镜按照Golay-3 阵列排列组成，系统分辨率为0.35″，视场为3'［4］。

目前菲索式合成孔径干涉阵列成像技术在国内还处于理论分析和样机筹备阶段。国家天文台、中科院南京天文仪器研制中心承担的863 预研项目曾开展综合孔径理论的研究。国家天文台主要开展了地基光学系统对天观测的研究工作。哈尔滨工业大学开展了光学多孔径技术及其应用的预研工作。苏州大学、航天科技集团第五研究院508 所和北京理工大学在973 重大基础研究项目的支持下，承担了“甚高分辨率空间遥感器的研究”课题。苏州大学现代光学技术研究所近年来开展了稀疏孔径复杂光瞳光学系统成像理论的研究［5］。

本文针对Golay-3 阵列菲索式合成孔径望远镜进行光学系统设计，用小口径光学系统获取大口径光学系统的分辨率。与以往菲索式合成孔径干涉阵列望远镜相比，系统具有较大的视场(0.2°) ，有利于对快速移动目标的捕获与跟踪。

2 干涉阵列

菲索型合成孔径望远镜之所以被称为“像面干涉”型望远镜，是因为系统中来自不同子孔径的出射光束在同一光束组合器像面干涉成像，如图1 所示。它的子孔径是独立的望远镜，用于离散采集空间频率信息，其排列方式决定了系统对空间频率的覆盖状况［6］。

图1 菲索型合成孔径望远镜系统结构Fig.1 System structure of Fizeau-type synthetic aperture telescope

光学系统分辨率取决于系统MTF 覆盖的空间频率截止频率: 截止频率越大光学系统分辨率越大，因此好的子孔径干涉阵列要追求系统MTF截止频率最大化。到目前为止，比较好的干涉阵列主要有以下几种:环面( Annulus) 、环型( Ring) 、戈莱( Golay) 型、三臂( Tri-Arm) 型、等边六孔径型、复合三子镜［7］。

子孔径数目越多，阵列对空间频率u-v 优化覆盖越好，MTF 截止频率越高，但系统的复杂度越高，相应的子孔径支路间光程差调制越难，同时也会出现越多的机械误差。另外，用于快速移动目标捕获与跟踪的望远光学系统安装在经纬仪跟踪架平台上，其头部重量和尺寸受到跟踪架的限制，子孔径数目不能多于5 个，否则头部转动惯量势必增大，不利于稳定跟踪［8］。

在兼顾空间频率u-v 覆盖和系统简单化前提下，本文选择Golay-3 型干涉阵列，如图2 所示。其中r为子孔径半径，L为干涉阵列中心至子孔径中心的距离。

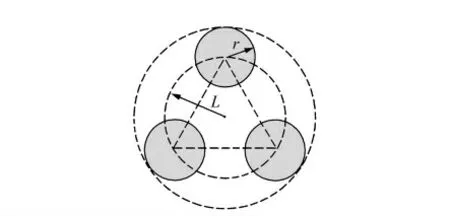
图2 Golay-3 型干涉阵列Fig.2 Interference array of Golay-3 type

2.1 填充因子

填充因子定义为子孔径面积和与阵列外切圆面积的比值，用F表示，它反映了子孔径阵列的紧密程度。

当子孔径相切时填充因子最大，Golay-3 的最大填充因子Fmax=0.65。随着填充因子变小，即子孔径阵列的排列越来越稀疏，光学系统对空间频率的覆盖范围越大，系统MTF 截止频率越高，系统分辨率越大。但是填充因子变小时，MTF 的中频段响应值会降低，并在填充因子足够小时降为零，此时光学系统分辨率将由MTF 第一个零点而非截止频率位置决定，也就是单孔径的分辨率(0.61λ/r)［9］。与单个子孔径相比，合成阵列分辨率并没有增大，只是增加了光束能量采集度。由以上可得Golay-3 阵列的填充因子范围为0.33≤F≤0.65。

在确定干涉阵列结构时，既要尽量选取小的填充因子获取高分辨率，又要避免空间频率中频段相应过低引起的成像模糊。本设计选取L=1.6r，填充因子F=0.44。

2.2 系统等效分辨率

传统的像质评定标准( 如分辨率、能量集中度) 不适用于干涉阵列光学系统。观测扩展物体时，光学系统的评价标准不仅要用点扩散函数( PSF) ，还需要能够评价扩展目标调制传递特性的调制传递函数( MTF)［10］。而且，干涉阵列光学系统的空间分辨率在成像平面上随方向的变化而变化，呈二维分布的MTF 正好可以反应干涉阵列光学系统的二维分辨率。此处定义系统的等效口径为MTF 截止频率与合成孔径系统MTF 最小截止频率相等的单孔径系统的口径［14］。选用系统最小截止频率对应的口径作为合成孔径系统的等效口径是保守算法。图3 为Golay-3 阵列光学系统MTF 的空间频率覆盖二维图。

图3 Golay-3 阵列MTF 的空间频率覆盖图Fig.3 Spatial frequency coverage of MTF for Golay-3 array

其中d= 3L为两个子孔径的中心距，D=2r为子孔径直径，R/λf为最小截止频率。由三角关系可以求出:

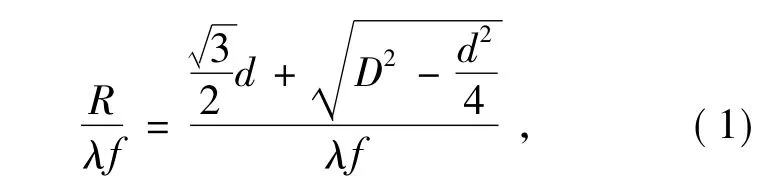
即最小截止频率对应的等效口径为:

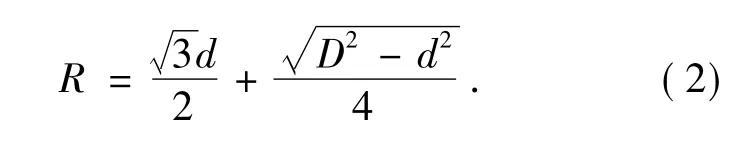
此设计选取r=150 mm，L=240 mm，可以算出等效口径R=576 mm。

3 光学系统设计

菲索式合成孔径望远镜光学系统可以分成三部分来设计:第一部分是用于能量采集和角度放大的无焦子孔径; 第二部分是调节光程与校正角度的光束控制器; 第三部分是负责成像的光束组合器。

3.1 子孔径的光学设计

干涉阵列中的子孔径为无焦望远系统，用于能量采集、光束压缩和入射光束角度放大，其口径为300 mm，视场2ω =0.2°，角放大倍率为10，工作于可见光波段，用F，d，C光进行系统优化。

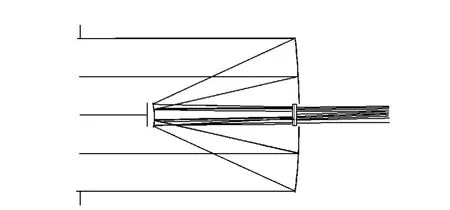
图4 子孔径结构图Fig.4 Structure diagram of subaperture

选用后接双胶合消色差负透镜的卡塞格林结构，主镜是抛物面，次镜为双曲面，选用BK7 和SF2［12］玻璃，如图4 所示。次镜的中心遮挡会造成子孔径通光面积减少2%，引起空间频率低频段略有降低，但不影响系统分辨率。

运用zemax 的无焦系统分析功能进行分析，其弥散斑皆在爱里斑内，波前RMS 误差为0.065λ(d光，0.0707°视场) ，系统MTF 曲线接近衍射极限，如图5 所示，可实现对F，C光消色差。

图5 子孔径系统MTF 曲线Fig.5 MTF curves of subaperture

3.2 光束控制器

光束控制器的作用是使各个支路光束在入射到组合器入瞳面时保持等光程和平行，因而光束控制器要有光程调节和光束角度调节两个环节。

为了实现控制简单化，光程调节和角度调节要相互独立，即调节光程时不会引起角度变化，反之亦然。因此，要将光程调节器做成呈90°折角的内反射镜以满足要求，如图6 所示。

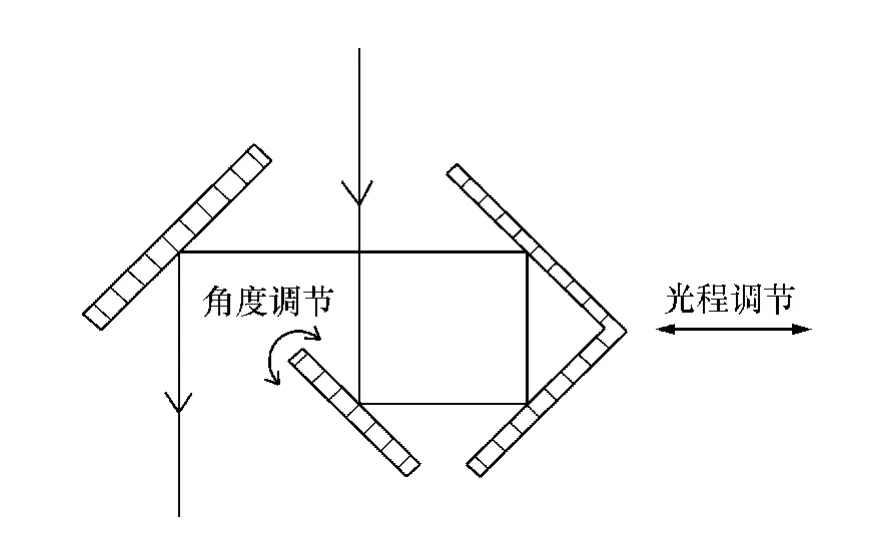
图6 光束控制器Fig.6 Structure diagram of ray controller

3.3 光束组合器的光学设计

各个子孔径的出射光经过多次反射后入射到光束组合器的入瞳，最终在光束组合器像面干涉成像。子孔径的出射角即光束组合器的入射角(1°) 。光束组合器的入射光束在入瞳处的排布是子孔径排布的缩放，缩放因子等于子孔径的角放大率的倒数［13］。组合器入瞳直径为100 mm，视场2ω=2°，F/#=6，工作在可见光波段。

大孔径长焦距系统主要校正球差、彗差、轴向色差［12］。选用高折射率玻璃可以减小光线入射角，降低高级像差，偏离P-ν 普遍线的玻璃可以实现复消色差［14］。沿光线传播方向，玻璃材料依次为ZF3_cn，ZK14_cn，ZF6_cn，LAF5_cn，ZBAF8_cn，其中LAF5_cn 的部分色散PdC=0.271 9、阿贝数νd=37.639 2，满足复消色差要求。

初始结构为三片式复消色差结构，孔径为50 mm，焦距为600 mm，采用逐渐增大孔径和添加玻璃方式进行优化。最终结构图如图7 所示。

图7 光束组合器结构图Fig.7 Structure diagram of ray combiner

系统为五片式结构，总长为604.049 mm，波前RMS 误差为0.005 3λ(d光，0.707°视场) ，实现对F，d，C光复消色差，MTF 曲线接近衍射极限，图8、图9 分别为系统MTF 曲线和色差焦移图。

图8 光束组合器MTF 曲线Fig.8 MTF curves of ray combiner

图9 光束组合器色差焦移图Fig.9 Chromatic focal shift curve of ray combiner

4 结果与分析

4.1 总系统组合

在zemax 非序列中将子孔径和光束组合器进行组合，总系统通光孔径为环形，最大半径为390 mm，最小半径为90 mm，视场2ω=0.2°，焦距为6 000 mm。系统入射光是平行光，依次经过子孔径的主镜、次镜的两次反射和双胶合负透镜折射后光束直径压缩为1/10，角度放大10 倍，再经过光束控制器做角度和光程差校正后到达光束组合器入瞳，并最终在组合器像面成像。系统结构图如图10 所示。

图10 总系统结构图Fig.10 Structure diagram of total system

4.2 像质评价

对比总系统和单个子孔径的点扩散函数弥散斑( 如图11) 和调制传递函数( 如图12) 可以看出，总系统的点扩散函数中心弥散斑相比于单个子孔径系统明显减小，从24 μm 减小为8.3 μm。总系统的MTF 截止频率T分量为250 cycle/mm，S分量为189 cycles/mm( 也是总系统最小截止频率) ，远高于单个子孔径系统的100 cycle/mm。说明总系统分辨率远高于单个子孔径系统的分辨率。

图11 点扩散函数图Fig.11 Diagram of PSF

图12 MTF 曲线Fig.12 Curves of MTF

总系统点扩散函数除中心弥散斑外还有6 个旁瓣，从而使总系统实际分辨率要低于用点扩散函数中心弥散斑直径计算得到的分辨率，所以普遍选用MTF 来评价系统分辨率。在具体的计算方式上存在不同的观点，此处选用总系统MTF 最小截止频率作为等效全口径系统的截止频率。

总系统MTF 最小截止频率为单孔径系统截止频率的1.89 倍，相应的总系统等效口径也是单孔径的1.89 倍，即576 mm，这与式(2) 求得的无像差理想系统等效口径为576 mm 是吻合的。由等效截止频率可以求得中心波长550 nm 下系统等效分辨率为0.24″。

4.3 讨 论

从上面的像质分析可以看出，合成孔径点扩散函数除主峰外还有6 个次峰，反映在MTF 上就是高频段的T、S分量分离，这是合成孔径干涉阵列望远系统的固有缺陷。合成孔径干涉阵列望远镜的光瞳函数是对光瞳面的间断采样函数，存在的不足是对空间频率中频段信息的采集量降低，相对应的调制传递函数中频段响应值会降低，点扩散函数的旁瓣会较大。这些反映在像面上就会造成图像模糊，且图像信噪比下降，因此必须开发与干涉阵列光学系统相匹配的图像复原算法，提高光学系统对中频段信息的传递能力［15］。

虽然，此光学系统子孔径排列方式为Golay-3阵列，但是，由于系统分成3 个模块进行设计，可以根据实际需要方便地改变子孔径阵列结构。光束控制器与子孔径绑定，随子孔径数目和排列方式改变而改变。子孔径阵列改变时，只需调整光束组合器入瞳前的反射镜以保证光束在光束组合器入瞳处的排列方式为子孔径入瞳的等比例缩放( 缩放因子等于子孔径的角放大率) 即可。

另外，光路中还要增加自适应光学系统，测量子孔径支路间光程差和光束倾斜误差，进而反馈到光程调节器和角度调节器，保证光束组合器入射瞳处光束的等相位和平行性，这有待后续研究。

5 结 论

为了以小口径子孔径获得等效大孔径的分辨率，本文对Golay-3 阵列合成孔径望远镜系统进行光学设计，增大系统视场，以便对高速移动目标进行捕获与跟踪，而采用模块化设计利于子孔径阵列扩展。

设计选择的子孔径阵列为最简单的Golay-3阵列，填充因子F=0.44。将系统分成3 个子系统并分别进行光学设计后，将各个子系统组合并对总系统的像质进行分析。像质分析结果: 总系统分辨率为0.24″，实现了以300 mm 口径子孔径获取等效口径576 mm 系统的分辨率。

［1］ RABB D J，JAMESON D F，STAFFORD J W，et al.. Multi-transmitter aperture synthesis［J］.Opt． Express，2010，18(24) ：24937-24945.

［2］ BELLE G T，MEIN A B，MEINEL M P. The scaling relationship between cost and aperture size for very large telescopes［J］.SPIE，2004，5489：563-570.

［3］ ADEN B M，MARJORIE P M. Large sparse aperture space optical systems［J］.Opt． Eng，2002，41(8) ：1983-1994.

［4］ 乔彦峰，刘坤，段相永.光学合成孔径成像技术及发展现状［J］.中国光学与应用光学，2009，2(3) :175-183.QIAO Y F，LIU K，DUAN X Y. Optical synthetic aperture imaging techniques and development［J］.Chinese J． Opt． Appl． Opt．，2009，2(3) :175-183.( in chinese)

［5］ 王晓明，乔彦峰.地基多孔径成像系统验证试验设计［J］.中国光学与应用光学，2010，3(6) :671-678.WANG X M，QIAO Y F. Design of foundation multi-aperture imaging system validation experiment［J］.Chinese J． Opt．Appl． Opt．，2010，3(6) :671-678.( in Chinese)

［6］ RABB D，JAMESON D，STOKES A，et al.. Distributed aperture synthesis［J］.Opt． Express，2010，18( 10) : 10334-10342.

［7］ 郭勇.稀疏孔径光学系统阵列结构的优化［D］.苏州:苏州大学，2007.GUO Y. Optimization of the optical sparse array configuration［D］. Suzhou:Suzhou University，2007.( in chinese)

［8］ 杨立保，李艳红，王晶，等. 多镜头成像拼接方法在经纬仪系统中的应用［J］. 光学 精密工程，2010，18( 5) :1048-1053.YANG L B，LI Y H，WANG J，et al.. Application of multi-lens image stitching to opto-electronic theodolites［J］.Opt．Precision Eng．，2010，18(5) :1048-1053.( in Chinese)

［9］ 吴泉英，钱霖.类Golay6 稀疏孔径结构［J］.光学 精密工程，2010，18(7) :1453-1459.WU Q Y，QIAN L. Pupil configuration of quasi-Golay6 sparse-aperture［J］.Opt． Precision Eng．，2010，18( 7) :1453-1459.( in Chinese)

［10］ 韩骥，王大勇，刘汉承，等.光学稀疏孔径成像复合孔径阵列结构研究［J］.光电子·激光，2007，18(6) :649-652.HAN J，WANG D Y，LIU H C，et al.. Multiple-array configuration design of optical sparse-aperture imaging system［J］.J． Optoelectronics Laser，2007，18(6) :649-652.( in Chinese)

［11］ CHUNG S J，MILLE D W. ARGOS testbed:study of multidisciplinary challenges of future spaceborne interferometric arrays［J］.Opt． Eng．，2004，43(9) :2156-2167.

［12］ GEARY J M.Introduction to Lens Design:with Practical Zemax Examples［M］. Richmond，Virginia:Willmann-Bell Inc，2002:175-185.

［13］ 王治乐，张伟.斐索型光学合成孔径系统近轴成像条件研究［J］.应用光学，2004，25(5) :3-6.WANG ZH L，ZHANG W. Study on Fizeau optical synthetic aperture paraxial imaging［J］.Appl． Opt．，2004，25(5) :3-6.( in chinese)

［14］ 王之江.光学设计理论基础［M］.上海:科学出版社，1965:310-335.WANG ZH J.Fundamentals of Lens Design［M］. Shanghai:Science Press，1965:310-335.

［15］ 李波，李艳，李昕.稀疏孔径光学系统成像的图像恢复算法研究［J］.光子学报，2010，39(2) :275-278.LI B，LI Y，LI X. Research on the image restoration for sparse aperture optical systems［J］.Acta Photonica Sinica，2010，39(2) :275-278.