梁格法在单箱多室箱梁桥结构分析中的应用

胡朝辉，王爱云

(1.广州诚安路桥检测有限公司，广东广州510006;2.广东技术师范学院天河学院，广东广州510540)

单箱多室箱梁具有整体性能好、抗扭刚度大、弯曲应力图形合理、剪应力小［1］等优良的截面特性，且能方便地适应线路的宽度变化，在桥梁结构中得到越来越广泛的应用。此类桥梁一般宽跨比数值较大，空间受力的特性较为突出，采用传统的平面杆系单梁法计算，有可能产生较大误差。梁格法是一种空间计算的近似方法，其核心思想是利用等效的纵、横梁格代替桥梁上部结构，将分散在板、梁每一区段内的弯曲刚度和抗扭刚度集中于最邻近的等效梁格内。梁格法可直接输出各主梁的内力，便于进行结构的分析验算，因而比板壳与实体单元具有更强的直观性和适用性，但梁格法的精度很大程度上取决于梁格单元的划分，目前对梁格单元的刚度取舍仍然是较为棘手的问题。本文以一座单箱多室宽箱梁桥的结构分析为例，结合现场荷载试验数据，对梁格法的特点及梁格刚度的取舍作出探讨与验证。

1 工程概况

广州市某主线高架桥位于广州市新光快速路的赤岗路段。桥梁分左右两幅，横向为1 m宽后浇带联结，其中一联桥跨径组成为(30.0+45.0+30.0)m，桥面宽22.6 m，单向5车道，上部结构采用变截面现浇预应力混凝土连续箱梁，横断面为单箱四室。梁高为2.0～2.5 m，顶板厚度为0.22 m，底板厚度为0.22～0.35 m，边腹板厚度为0.45～0.65 m，中间腹板厚度为0.35～0.55 m，各跨墩顶和跨中设置横梁，箱梁混凝土为C50，设计荷载等级为城－A级。

2 模型建立及结果分析

2.1 有限元模型

采用梁格法对该桥进行有限元分析，建模时进行如下处理。

(1)纵梁:将箱梁划分为5片纵向梁格，忽略由于截面分割带来的形心位置与腹板中线的偏差。5片纵梁的位置分别对应箱梁腹板中线，为了保证计算精度，纵向梁格划分不宜过于稀疏，但过密亦会加大计算量，且对精度的提高已不明显。这里纵向梁格取1 m，横向梁格间距亦为1 m，各纵梁截面中和轴与整体截面中和轴应保持一致。

(2)横梁:横梁分为刚性梁与虚拟梁。虚拟梁可采用工字形梁，顶底板分别取箱梁上下翼板厚度，腹板厚度取极小的值，以达到对横向联系梁的模拟。对于跨中及墩顶部位的横隔板，则采用刚性横梁模拟。依据梁格理论，箱梁经划分成为梁格之后，截面形状由闭口到开口，其扭转刚度差异很大，因此需调整纵横梁的扭转刚度，纵梁及虚拟横梁每单位宽度的扭转常数可按下式计算［2］:

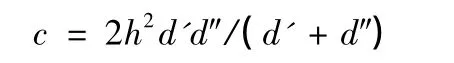
式中:d'、d″、h分别为顶、底板的厚度和梁高，纵向梁格的剪切面积则取腹板的横截面积。

(3)桥面铺装:大量的荷载试验表明桥面铺装不同程度地参与了主梁的结构受力，为考虑其对箱梁整体刚度的影响，可在梁格模型上建立辅助的板单元，板厚的选取则需考虑桥面铺装与箱梁材质、边界及联结强度的异同，也可将箱梁顶板适当加厚，但会因箱梁截面中性轴整体上移而带来误差。

此外还需在箱梁两端翼缘处设置纵向虚拟梁格，此举是为了准确计算自振周期和分配荷载。箱梁的纵向梁格划分见图1所示，采用MIDAS/CIVIL与ANSYS软件分别建立该桥的梁格模型与实体模型，并进行设计活载及试验荷载内力、试验荷载反应和自振特性的分析计算。

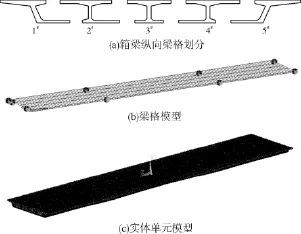
图1 有限元模型

2.2 试验结果分析

为了获得结构试验荷载与变位关系的连续性和防止结构意外损伤［3］，加载方式为单次逐级递加到最大荷载，然后一次卸到零级荷载。加载位置与加载工况确定的主要依据是尽可能用最少的加载重车满足试验荷载效率。静载试验采用4台重约35 t的加载车，分6个工况，通过工况3、工况4、工况6，分别可使边跨跨中正弯矩、中支点负弯矩、中跨跨中正弯矩达到加载效率。试验过程中，量测结构控制截面的静力位移、应变、裂缝等静态参数;在动载试验中，利用地脉动、跑车、跳车等工况激起桥梁结构的振动，量测桥梁结构的固有频率、阻尼比、振型等模态参数［4］。限于篇幅，这里仅列出各控制截面最大荷载工况下的挠度值，见表1所示。各工况下的纵、横桥向挠度曲线及应变曲线如图2、图3所示。

表1 最大荷载试验工况下各模型挠度计算值与实测值对比(单位:mm)

图2 最大荷载工况下纵、横桥向挠度曲线

图3 最大荷载工况下边跨、中跨跨中应变曲线

由上面图表中结果可看出，各试验工况下两种模型的计算结果较为接近，两者得出的中跨跨中最大挠度分别为4.5 mm和4.6 mm，其余纵向挠度测点数值相差也很小，梁格模型和实体模型的横向分布曲线与实测值曲线较为吻合，实测挠度及应变均小于理论值，也表明了该联桥受力合理，具有一定的安全储备。另外，在动测试验中，该联桥实测一阶固有频率为3.17 Hz，阻尼比为0.8895% ～2.9528%，对应梁格模型的一阶固有频率为3.05 Hz，实体模型为3.12 Hz，实测频率较理论计算值大，说明该联桥整体刚度较好。由此可见，本文的梁格划分在纵横梁刚度取值上是合理的。

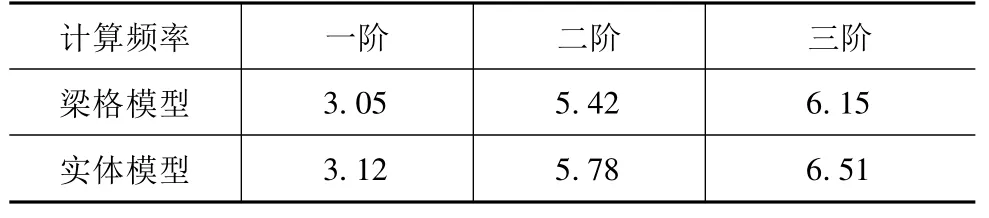
表2 梁格模型和实体模型计算频率 (单位:Hz)

2.3 对横梁刚度取值的一些探讨

由横桥向挠度及应变曲线可知，相比梁格模型，实体单元挠度及应变的横向分布趋势与实测曲线更为接近，也即对横向联系的模拟实体模型较梁格法精确些，因此实际建模当中，可以考虑用实体单元的数值结果来对梁格模型的横梁刚度进行修正，一般只需调整其刚度至其计算结果能满足精度要求即可。另外，虚拟横梁的扭转刚度亦有助于纵梁的抗弯承载力，忽略横梁的抗扭刚度亦会加大计算误差。对于此类多室箱梁的横梁抗扭刚度，亦需看作闭口截面来考虑，因此需对模型中的虚拟横梁抗扭刚度进行修正，可参照文献［2］给出的计算方法。

通过算例不难得知，在此类多室箱梁桥中运用梁格法，关键之处不外乎纵、横梁抗弯、抗剪及抗扭的准确模拟。对于纵梁的抗弯、抗剪、抗扭刚度在文献［2］均有准确的计算方法。然在虚拟横梁的刚度取值上仍无规范的办法，大部分都根据工程经验来取舍。特别在具有多片梁的或正交、或斜交以及斜弯的整体式或装配式宽桥当中(如空心板、T梁、小箱梁)，更难以定夺虚拟横梁刚度值，因此对横梁特性取值问题，还有待作更深入的探讨。

3 结论及建议

本文通过对某单箱多室连续宽箱梁桥的结构分析及与现场荷载试验实测数据的对比分析，得出如下主要结论:

(1)对于多室箱梁桥梁格分析，应据其结构特点对纵梁和横梁的抗弯、抗扭刚度进行修正，必要时还应对横梁的抗剪刚度进行修正，以保证纵横梁的刚度与切分前等效;

(2)箱梁桥梁格中的虚拟横梁可取工字形截面，顶底板与箱梁顶底板同厚度，腹板取一极小值，可以较准确地模拟其横向传递。必要时可据实体单元模型计算结果对其刚度进行修正，一般只需调整其刚度至其计算结果能满足精度要求即可;

(3)与实体单元相比，梁格模型建模方便，计算量小，后处理中能够直接提取结构内力，便于进行结构分析验算。但对横梁刚度的取值目前尚无规范的方法，亦即不能实现梁格的“完全等效”，因此就横梁特性取值问题还有待进一步研究。

［1］(捷)V·克里斯特克.箱梁理论［M］.何福照，吴德心，译.北京:人民交通出版社，1988

［2］(英)E·C·汉勃利.桥梁上部构造性能［M］.郭文辉，译.北京:人民交通出版社，1982

［3］张俊平.桥梁检测［M］.北京:人民交通出版社，2002

［4］交通部科学研究所.大跨径混凝土桥梁的试验方法(试行)［S］

［5］邵旭东.桥梁工程(第二版)［M］.北京:人民交通出版社，2007