带有舵机特性的船舶航向自动舵DSC-MLP设计

刘程，李铁山，陈纳新

(1.大连海事大学 航海学院，辽宁大连116026;2.上海交通大学船舶海洋与建筑工程学院，上海200240;3.大连海事大学数学系，辽宁大连116026)

近年来，航运业迅速发展，对于船舶航行安全、节能、降低船员的劳动强度的要求日益增强，所以船舶航向控制问题得到了大家的关注.尤其是从70年代以来，各种控制技术不断应用于航向控制，如自适应控制［1-2］、H∞控制［3-5］、鲁棒控制［6-8］以及先进智能控制［9］等.然而，迄今为止，很多控制算法还不能应用于工程实际.究其原因主要是一方面，船舶动态具有高度非线性、长时滞、大惯性等特性，同时风、浪、流等外扰的随机性以及航行工况(装载、航速等)的频繁变化使船舶运动数学模型呈现明显的不确定性.这些特性使得很多控制算法不能适用;另一方面，一些控制算法本身由于算法复杂、计算负担重，在线执行耗时明显而限制了其在工程实践中的应用.因此，研发易于工程实现的自动舵控制算法正成为目前船舶控制领域的一个研究热点.

本文针对带有舵机特性的非线性船舶航向控制系统，提出了一种计算量小、易于工程实现的自动舵控制算法.

利用Lyapunov方法证明了闭环系统的稳定性，并通过计算机仿真验证了方法的有效性.

1 问题的提出

非线性船舶航向控制系统数学模型的舵角δ和航向φ的关系可以用下面的数学模型描述:

式中:K、T分别表示时间增益和时间常数，它们都是船舶前进速度和船长的函数.H(φ·)是φ·的非线性函数，可以近似表示为［10］

式中:ai(i=1，2，3，…)是实值常数.

由于船舶的舵机系统无法实现阶跃操舵，忽略舵机特性将影响控制系统的性能品质［11］.因此，从实际应用来看，为了获得良好的航向控制性能，还应考虑舵机伺服系统的特性.船舶舵机的动力特性可以描述为

式中:δE为舵机发出的命令舵角，δ为实际舵角，KE为舵机控制增益，TE为舵机时间常数.

定义 x1=φ，x2=，x3= δ及 u= δE，由式(1)、(3)可得到包含舵机特性的非线性船舶航向控制系统模型:

式中:f2=－(1/T)H)，g2=K/T，f3= － (1/TE)，g3=KE/TE.

本文的目标是针对系统(4)设计一种简单、计算量小的自适应模糊控制器使闭环系统的所有信号都有界，且使跟踪误差z1=x1(t)－yd(t)能够任意小.

首先，对上述系统做如下假设:

假设1 控制增益gi(i=2，3)是严格正的或者负的，即满足不等式0＜bmin≤|gi|≤bmax，其中 bmin，bmax是上下界.不失一般性，假设0＜bmin≤gi.

假设2 系统函数f2和f3是完全未知的.

假设3 参考信号yd(t)光滑有界且具有2阶连续有界的导数，即存在一个正的常数B0，使得集合∏0∶B0}成立.

2 T-S模糊系统

一般来说，T-S型模糊系统可以按照以下K条模糊规则构造:

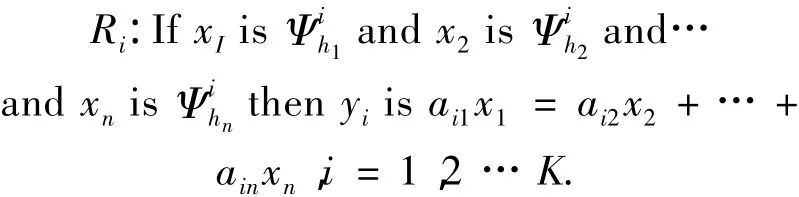
式中:aij(i=1，2，…，K;j=1，2，…，n)是未知常数，表示输入模糊变量.采用乘积模糊推理机评估ANDS模糊规则，经过中心平均解模糊器去模糊化，T-S模糊系统的输出可以表示为

式中:ξ(x)=［ξ1(x) ξ2(x) … ξK(x)］，ξi(x)=)］称为模糊基函数，(xj)称为模糊隶属度函数，矩阵

下面的引理1表明，T-S模糊模型可以做为通用函数逼近器，在任意的凸紧集上，以任意精度逼近任意光滑非线性函数［12］.

引理1 对于任意给定的连续函数f(x)，在论域U∈Rn内，∀ε＞0，存在一个如式(5)所示的T-S模糊系统x，Ax)，使得下式成立:

式中:ε 表示逼近误差［10］.

3 控制设计

由于系统(4)是一个非匹配系统，可以采用后推方法(backstepping)进行设计.而传统的后推方法在每一步都要对虚拟控制律进行重复求导，导致较高阶虚拟控制律和最终控制器所含项随着系统阶数的增加爆炸性膨胀，导致计算膨胀，从而限制了这种方法在实际工程中的应用.而动态面控制(DSC)方法［13］能够解决该问题.

现在将DSC思想融入后推方法，对系统(4)进行自适应模糊跟踪控制设计.其递归设计过程包含3步.在每一步，设计虚拟控制量ai+1.最后，在第3步，构造实际控制律.下面将给出设计的简要过程.

1)定义误差变量z1=x1－yd，则

将x2看做式(6)的虚拟控制量，并取其理想值，即虚拟控制律α2如下:

式中:k1是正的设计常数.

现在借助DSC思想，引入新变量s2，令α2通过带有时间常数η2的一阶滤波器［14］:

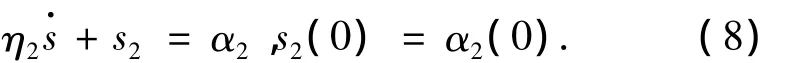
2)定义误差变量z2=x2－s2，则有

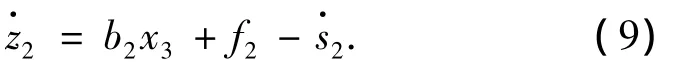
由于f2未知，采用T-S模糊系统(5)逼近，则有

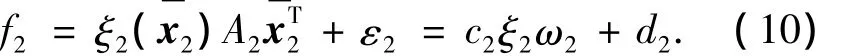
然后可得

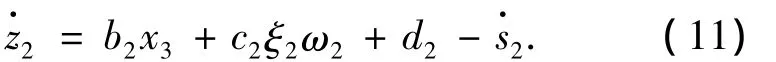
由于

类似地，选择虚拟控制律α3如下:

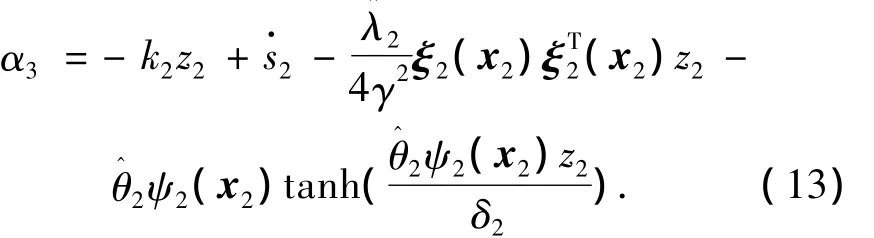
式中:λ2=;k2、γ2、δ2是设计参数;、分别是λ2和θ2的估计值，其自适应律将在后面给出.

现在引入变量s3，令α3经过时间常数为η3的一阶滤波器:

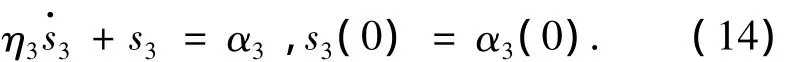
3)定义 z3=x3－s3，则有

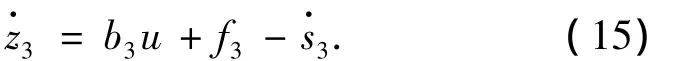
类似地，f3可以近似为

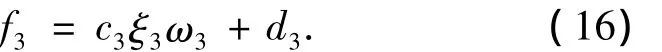
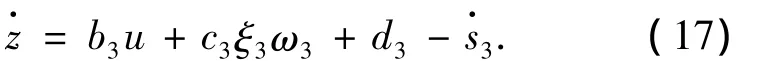
类似地

现在来选择控制输入u:

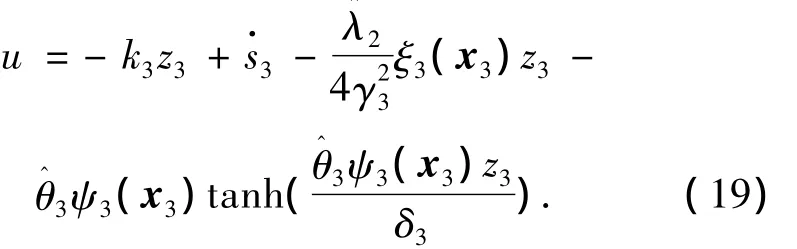
式中:λ3=;k3、γ3、δ3是正常数分别是λ3和θ3的估计值.

定理1 考虑由式(4)、(7)、(13)、(19)和(20)组成的闭环系统，如果给定一个正数p2，所有初步条件满足，(i=1，2，3).则存在 k、γ 、δ、iiiσi1、σi2、Γi1和 Γi2使得闭环系统的解有界.并且，对于任意给定的一个正数μ1＞0，可以通过调整控制器参数而使得跟踪误差充分小，即使得z1=y(t)－yd(t)满足|z1(t)|≤μ1.

证明 (略).

首先，定义一个新的误差变量:

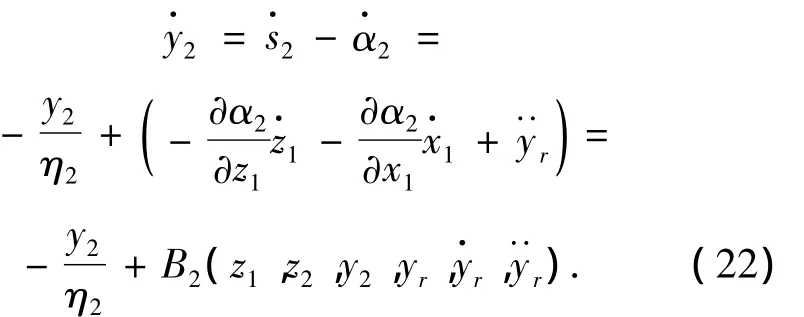
式中:B2(·)是式(22)右边的剩余项，是一个连续函数.类似地，有

同样，B3也是一个连续函数.

考虑到xi+1=zi+1+si+1和 si+1=yi+1+αi+1，整个误差系统可以表示为

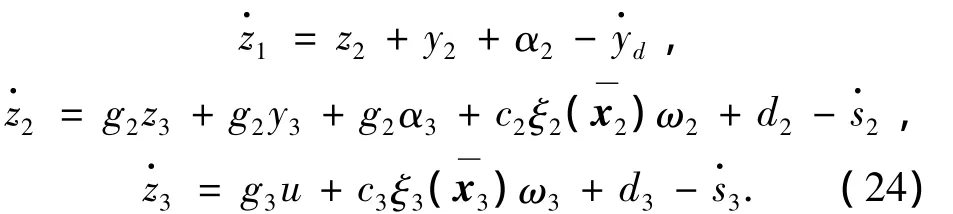
将αi+1(i=1，2)和控制输入u代入式(24)得

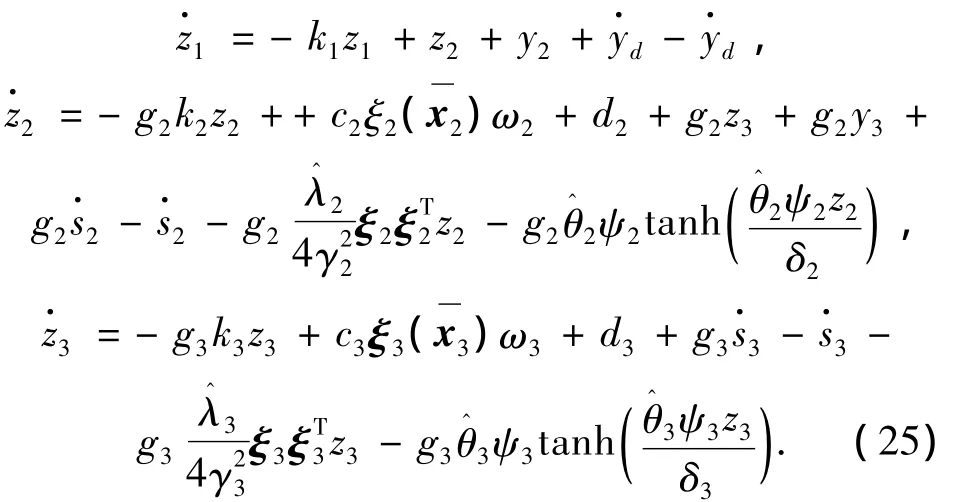
考虑如下Lyapunov预选函数:

注意到

由于 z2z1≤(z2/2)2+z21，y2z1≤(y2/2)2+z21，同时注= －y/n意到ii(i=2，3)，

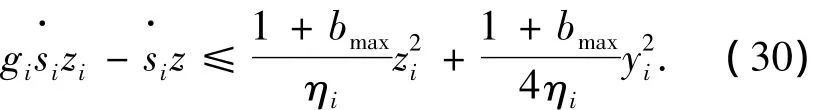
则式(27)变为

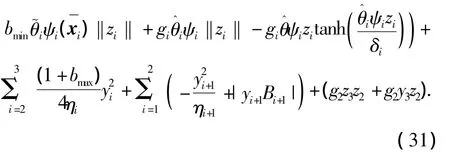
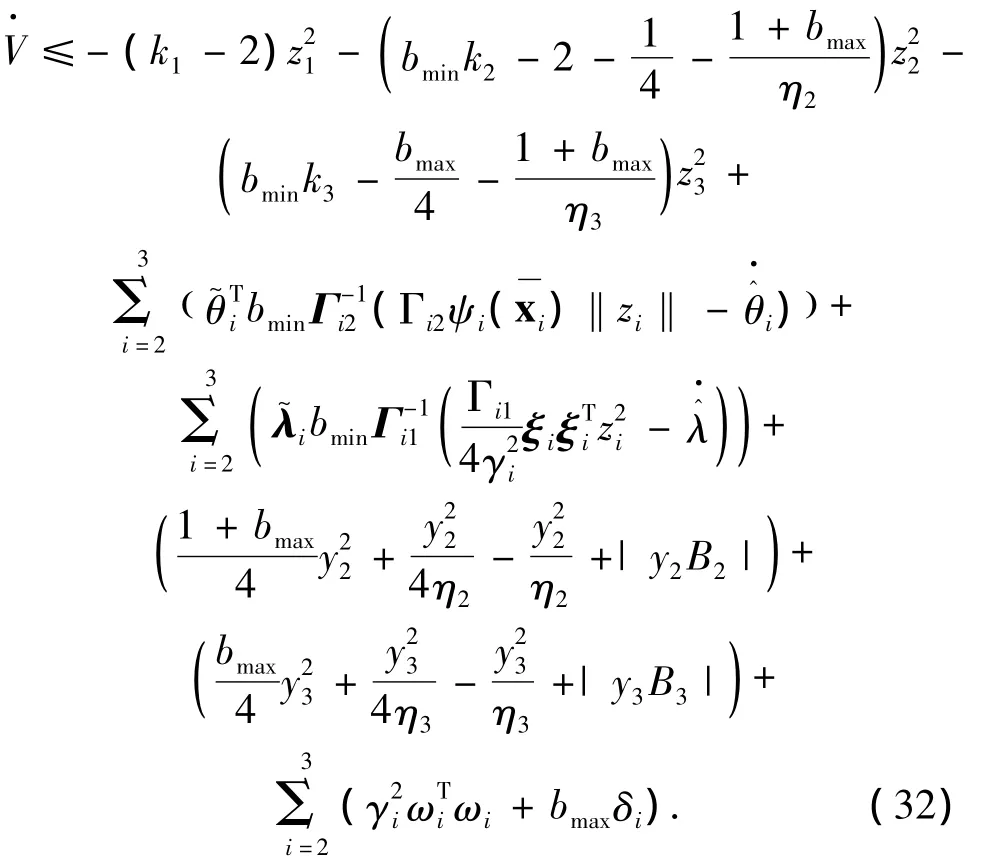
现在考察式(33)右边最后2项的属性.先考察Bi+1(i=1，2)的属性.

由于集合∏0∈R3和∏i∈)(其中 Nj是的维数)都是紧的，因此∏0×∏i∈i∈)也是紧的.因而|Bi+1|在∏0×∏i上具有一个最大值M［11］.

现在选取 σi1/2λmax(bmin)= σi2/2λmaxα0为一个正的常数.如果选择γ＜1，经过推导，则式(34)变为

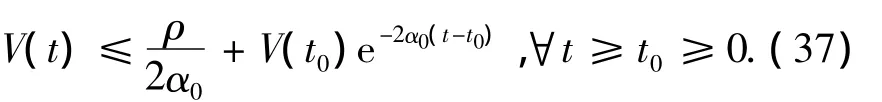
由上文可见，闭环系统的所有解都是有界的.并且，对于任意的 μ1＞(ρ/α0)1/2，存在一个 T ＞0，使得对于所有的t≥t0+T，都有‖z1(t)≤μi‖成立.这是因为通过选取适当的设计参数 k1、γ1、δ1、η2、σ11、σ12、Γ11和Γ12，可以使得(ρ/α0)1/2任意小.从而使得跟踪误差z1=y(t)－yd(t)尽可能地小.定理1证毕.

4 计算机仿真算例

在这部分，以大连海事大学远洋教学实习船“育龙”号进行仿真.其船型参数见文献［6］.跟踪信号选为能够代表某一实际性能要求的模型:

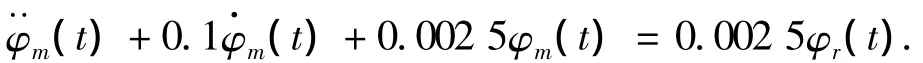
式中:φm表征了船舶航向的理想系统性能，而φr(t)是命令输入信号，其值从0到30°变化，以300 s为周期.

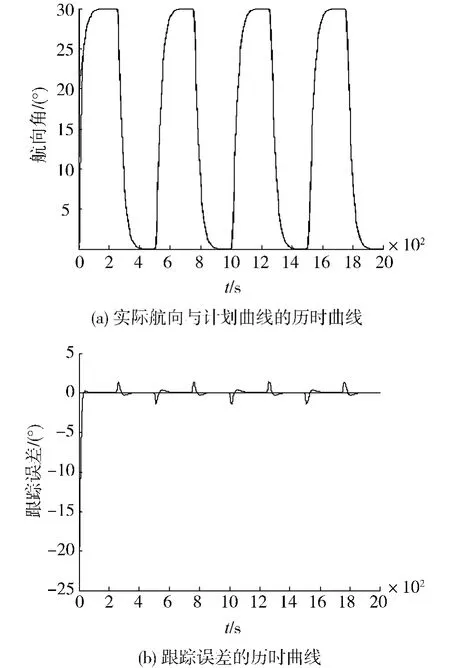
图1 航向跟踪控制与跟踪误差的变化曲线Fig.1 Curves of course-tracking control and tracking error

在仿真中，对于系统(4)中的每一个变量定义5个模糊集，分别标记为(NL)、(NM)、(ZE)、(PM)、(PL)，用以下隶属函数描述:

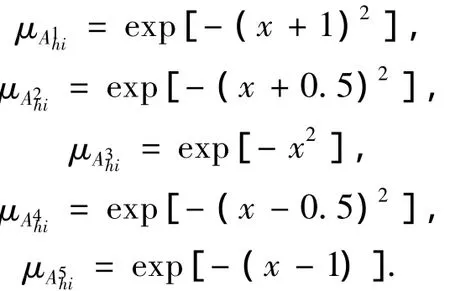
选取设计参数为 k1=0.1，k2=40，k3=5，Γi1=Γi2=2，σi1=σi2=0.001，==0，γi=0.5(i=2，3)，δ2=δ3=100.初始条件选取为:φm的初始状态为 20°，x1、x2、x3的初始状态都为零.仿真结果见图1、2.

图1表明航向跟踪效果理想且跟踪误差有界，图2表明输入舵角及舵角变化率都满足性能要求.

图2 控制舵角和舵角速率变化曲线Fig.2 Curves of control rudder angle and rudder angle rate

5 结束语

论文研究了船舶航向非线性系统的自适应跟踪控制问题.结合DSC和MLP技术，提出了一种自适应模糊控制算法，能够同时解决“维数灾难”和“计算膨胀”问题，学习参数少，计算量大为减少，易于在工程中实现.计算机仿真结果证明了算法的有效性.这种方法在工程实践中具有潜在的应用和推广价值.

［1］AMERONGEN JV.Adaptive steering of ships—amodel reference approach［J］.Automatica，1984，20(1):3-14.

［2］DU J L，GUO C.Nonlinear adaptive design for coursetracking control of ship withouta prioriknowledge of control gain［J］.Journal of Control Theory ＆ Applications，2005，22(2):315-320.

［3］贾欣乐，张显库.控制器应用于船舶自动舵［J］.控制与决策，1995，10(3):250-254.JIA Xinle，ZHANG Xianku.Controllers applied to autopilot for ships［J］.Control and Decision，1995，10(3):250-254.

［4］LIU S，YU P.Application of control to ship steering system［J］.Journal of Marine Science and Application，2006(1):5-9.

［5］CHENG Xiangqin，QU Jingyuan，YAN Zheping，et al.H∞robust fault-tolerant controller design for an autonomous underwater vehicle＇s navigation control system［J］.Journal of Marine science and Application，2010，9(1):87-93.

［6］罗伟林，邹早建，李铁山.船舶航向非线性系统鲁棒跟踪控制［J］.控制理论与应用，2009，26(8):893-895.LUO Weilin，ZOU Zaojian，LI Tieshan.Robust tracking control of nonlinear ship steering［J］.Journal of Control Theory and Applications，2009，26(8):893-895.

［7］卜仁祥，刘正江，李铁山.迭代滑模增量反馈及在船舶航向控制中的应用［J］.哈尔滨工程大学学报，2007，28(3):268-272.BU Renxiang，LIU Zhengjiang，LITieshan.Iterative sliding mode based increment feedback controland its application to ship autopilot［J］.Journal of Harbin Engineering University，2007，28(3):268-272.

［8］YUAN Lei，WU Hansong.Terminal slidingmode fuzzy control based onmultiple sliding surface for nonlinear ship autopilot system［J］.Journal of Marine Science and Application，2010，9(4):425-430.

［9］HU JQ，LIT S.Design of GA-based fuzzy control for ship steering［C］// Proceedings of WCICA， Dalian，China，2006.

［10］贾欣乐，杨盐生.船舶运动数学模型-机理建模与辨识建模［M］.大连:大连海事大学出版社，1999.

［11］郑云峰，杨盐生，李铁山.带有执行机构的船舶航向控制反馈线性化设计［J］.大连海事大学学报，2004，30(3):14-17.ZHENG Yunfeng，YANG Yansheng，LI Tieshan.Inputstate linearization based ship＇s course keeping controller designs［J］.Journal of Dalian Maritime University，2004，30(3):14-17.

［12］YANG Y S，ZHOU C J，LIT S.Small gainmethod for adaptive robust fuzzy control of a class of nonlinear systems［C］//Proc of the 2003 IEEE Int Symp on Intel Control，Houston，USA，2003:40-45.

［13］WANG D，HUANG J.Neural network-based adaptive dynamic surface control for a class of uncertain nonlinear systems in strict-feedback form［J］.IEEE Transactions on Neural Networks，2005，16(1):195-202.

［14］LITS，WANG D ，LIW.A novel adaptive NN control for a class of strict-feedback nonlinear systems［C］//2009 A-merican Control Conference，St.Louis，USA，2009:2946-2951.