吹除法对斜激波/边界层干扰控制数值模拟
孙润鹏,朱卫兵,黄舜,陈宏
(哈尔滨工程大学航天与建筑工程学院,黑龙江哈尔滨150001)
在超音速飞行的现代飞行器中,大都采用边界层泄除技术对进气道内存在的激波边界层干扰进行控制,通常的方法是采用边界层泄除装置和分流器,而这些方法在实际应用中均存在着明显的缺点[1-2],国外的研究者正试图找出一种替代办法来对进气道流场进行控制,其中包括边界层吹除控制、旋涡发生器控制、空腔循环控制、中央阻力片控制、流向狭槽控制和微射流控制等[3-8].R.H.Tindell等[9]利用激波发生器模拟进气道中激波边界层的干扰,实验设计了3组不同喷嘴用于调节吹除气体流量,通过测量总压恢复系数,研究了不同吹除流量和喷嘴位置对激波边界层干扰吹除控制效果,得出吹除方法能够对进气道内激波边界层干扰进行有效控制,可以达到与边界层泄除方法相同效果.另外,采用吹除法对激波边界层进行控制,所需压力较低,因此降低了对吹除控制设备的要求.基于此,本文对进气道激波边界层的干扰及边界层吹除进行了数值模拟,模拟采用了基于密度耦合的二维可压守恒型雷诺N-S方程,选取RSM湍流模型,Roe-FDS格式的对流通量,壁面处运用增强壁面函数法,收敛残差低于10-3.
文中首先模拟出边界层分离的现象,确定分离点位置,再根据分离点的位置选择吹除模型,最后用不同的吹除压力和吹除位置来分析吹除模型对抑制边界层分离的作用.经与实验结果比对证明模拟是准确的,本研究以求更深层次了解进气道内激波边界干扰特性,探讨了吹除压力和喷嘴位置对激波边界层的控制规律,为实际工程提供参考.
1 计算模型及数值方法
几何模型如图1所示,楔角9°,壁面攻角为0°,长度X=2.998 m.入口设为压力入口,入口总压0.7824 MPa;出口设为压力出口,出口静压 0.1 MPa.平板壁上采用边界层网格,首层网格高度为5×10-6m,以 1.05 的比率进行等比加密,共 100层,总网格数为62 101.来流Ma=2,流动考虑温度对粘性的影响,采用Sutherland定律.
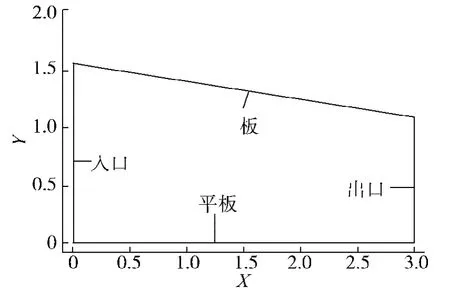
图1 平板/楔结构计算示意Fig.1 Schematic diagram of plate/wedge calculation
雷诺应力模型是求解雷诺应力张量的各个分量的输运方程.其具体形式为
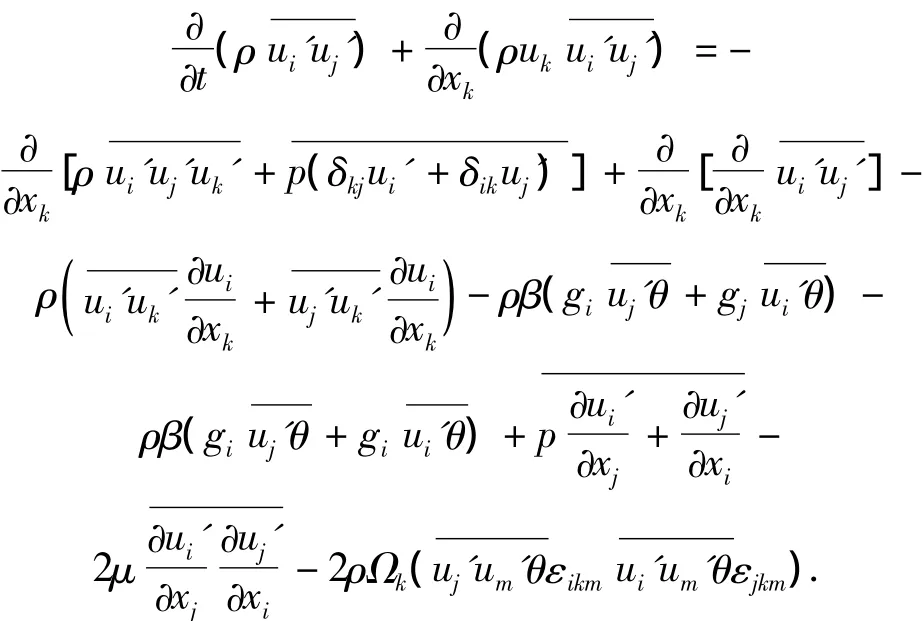
式中:Cij为对流项为湍流扩散项为分子扩散项,Pij为应力产生项,Gij为浮力产生项,Φij为压力应变项,εij为耗散项,Fij为系统旋转产生项.方程左边对流项Cij,及右边的,Pij,Fij不需要模拟,而、gij、Φij、εij需要模拟使方程封闭,其模拟项如下:
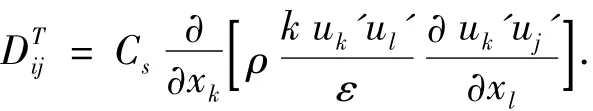
但这个模型会导致数值不稳定,因此程序中采用标量湍流扩散模型:
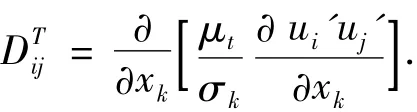
式中:湍流粘性系数用μt=ρCμ来计算,根据Lien and Leschziner的理论,σk=0.82.
根据Gibson and Launder得出的结论,压力应变项Φij可分解成3项,即
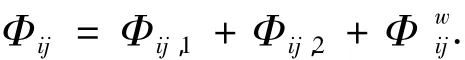
式中:Φij,1为慢压力应变项,Φij,2为快压力应变项,Φw壁面反射项.

壁面反射项用于重新分布近壁的雷诺正应力分布,主要是减少垂直于壁面的雷诺正应力,增加平行于壁面的雷诺正应力.
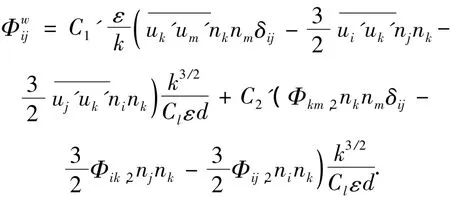
式中:C1'=0.5,C2'=0.3,nk是 xk在垂直于壁面方向上的单位分量,d是到壁面的距离,Cl=/k,Cμ=0.09,k=0.418 7.
当RSM雷诺应力模型用于平板流动壁面强化处理时,对 C1、C2、C1'、C2'进行修正,一次修正称为线性压力应变模型的低雷诺数修正.
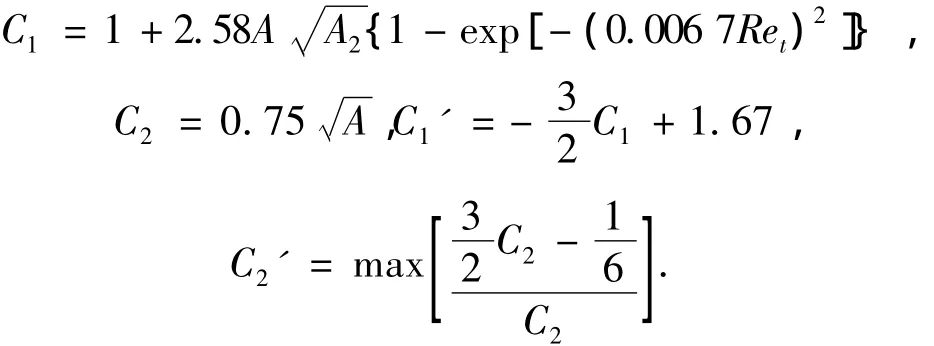
式中:Re为湍流雷诺数.A=tA2=aikaki,A3=aikakjaji,aij为雷诺应力各项异性张量,定义为

2 计算结果及分析
2.1 边界层分离
图2为无吹除时流场速度等值线图,由图可以看出,左下方一道前缘激波受左上方入射斜激波干扰,在壁面处形成了分离泡,分离泡的隆起迫使前方超声速气流向上偏转,从而在分离泡前产生一道分离激波,超声气流在分离泡后又被壁面强制偏转,从而产生再附激波,这两道激波之间出现了一组扇形膨胀波,该模拟结果与文献[10]采用Roe格式计算结果基本吻合,可以看出,流场波系结构非常复杂,本文的计算方法具有较高的激波分辨率及粘性分辨率,能较好的计算斜激波/边界层干扰问题.
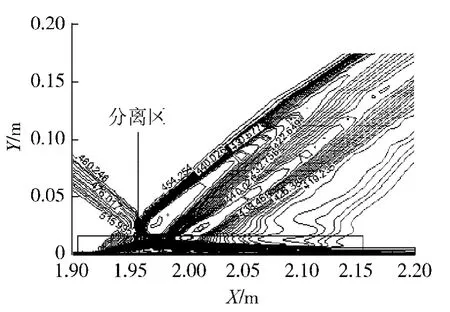
图2 速度等值线Fig.2 Velocity isoline
2.2 分离点确定
合理设置吹除喷嘴位置需确定分离区始点的位置,即分离点位置.在平板/楔结构中取若干X等值面,图3给出了各截面的速度分布.
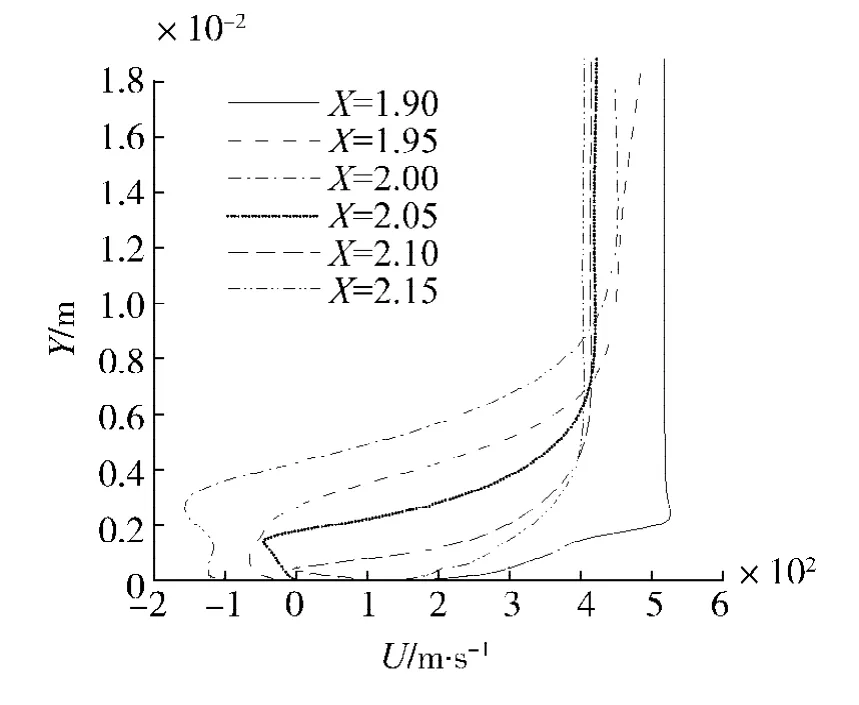
图3 速度截面Fig.3 Velocity section graph
由图3可知,X=1.90 m截面处速度均为正值,而X=1.95 m截面处速度出现了负值,这表明分离区起点存在于截面 1.90 ~1.95 m 之间.X=2.0 m截面处逆向速度变大,分离现象更加明显.在此之后,逆向速度又开始逐渐下降,从X=2.10m截面速度线可看出,其逆向速度接近于0.由此可推断出激波/边界层的分离核心区在X=2.0 m处附近,分离区范围在1.90~2.15 m之间.边界层内出现了分离区,且产生了很强的逆压梯度,该结果与Hakkinen[11]的实验现象一致,由此也可以证明RSM模型捕捉激波/边界层分离现象有较好的效果
2.3 吹除效果分析
在图1模型基础上加入吹除喷嘴模型见图4所示,喷嘴高度为20mm,以喷嘴设置在X=1.5 m处,吹除气流总压为0.5 P(P为主流总压)为例进行说明.为便于讨论,以AFS(after-facing step nozzle)代表加入吹除喷嘴状态,以WPC(wedge/plate configuration)为无吹除状态,Ps表示壁面气流静压,P0为主流入口静压.
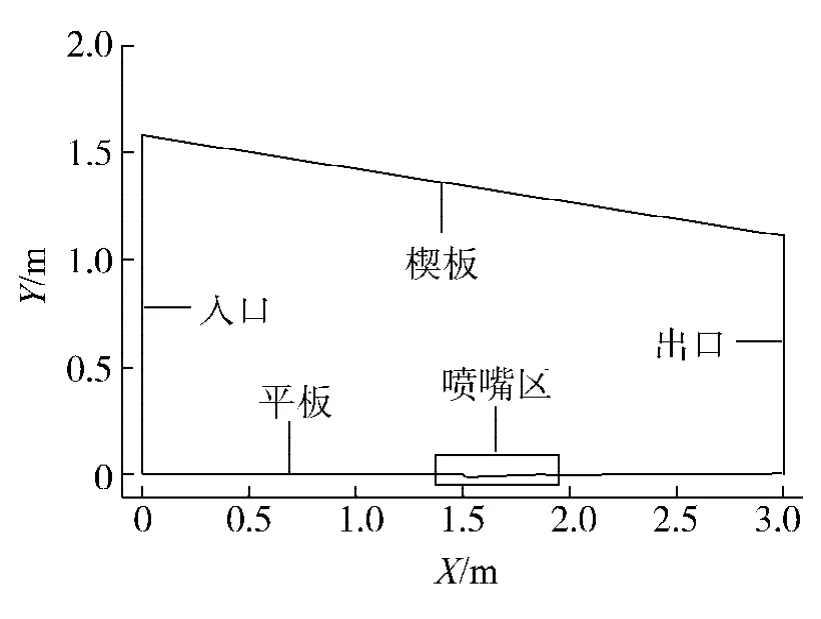
图4 吹除模型Fig.4 Blow ing model and grid
由图5壁面静压比可见,在分离点处虽然2种情况都存在压力突变,但加入吹除后,下游壁面静压比明显减小,由静压产生的逆压梯度降低,边界层内气流受到吹除气流加速作用,分离得到有效抑制.
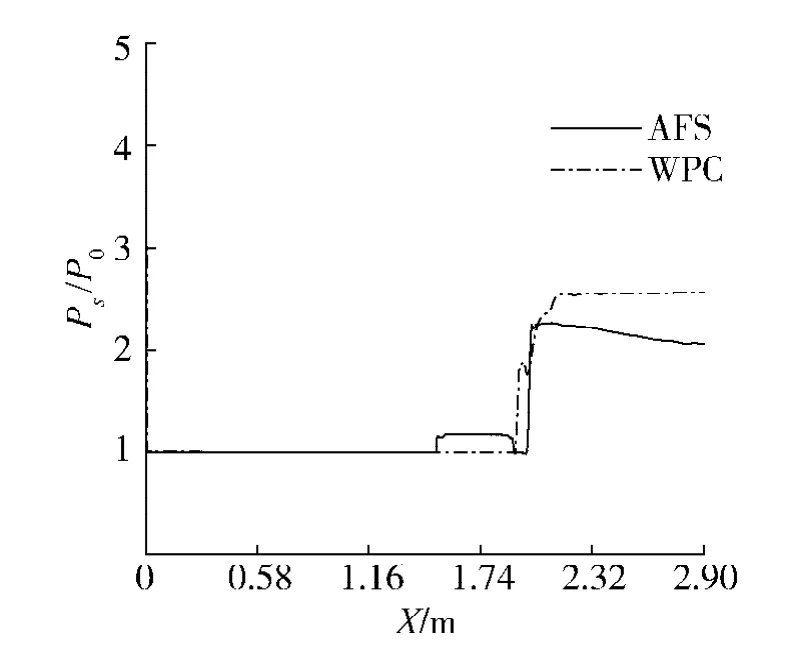
图5 静压比Fig.5 Static pressure area ratio
图6为壁面密度分布,加入吹除后,由于新气流加入,壁面密度有一急剧升高过程,混合完全后逐渐下降,在分离区受斜激波影响又有升高,此后沿分离区及下游壁面流体密度变化趋于平缓,密度值低于无吹除状态,流场相对稳定.由图5、6发现在X=1.5 m左右处,加入吹除后各参数均出现了一个小的突跃,随后又回落到正常水平.分析认为刚进入流场的吹除气体,气动参数尚不能迅速与主流匹配,随后受到喷嘴斜激坡的压缩,喷嘴壁面上的密度急剧增大,喷嘴斜激波位置见图7.
壁面摩擦阻力系数定义:Cf=τ/0.5,τ是流向方向上的壁面切应力,参考速度Uref为边界层边缘处势流速度.由图8壁面摩阻系数可以看出,加入吹除后,分离区下游壁面摩阻系数明显减小,且逐渐降低.另外,在下游某位置加入吹除装置,相当于对上游气流有泄除效果,边界层增厚,上游壁面摩阻系数也有较大程度降低,且变化平稳.

图6 密度分布Fig.6 Density distribution

图7 波系结构Fig.7 Wave system

图8 壁面摩阻系数分布Fig.8 Wall friction coefficient distribution
2.4 喷嘴位置效果分析
分别取喷嘴位置在 X 为1.3、1.4、1.5、1.6和1.7 m处,以了解喷嘴位置对边界层吹除效果的影响.


图9 不同喷嘴位置时壁面参数分布Fig.9 Wall parameters distribution of different nozzle positions
由图9(a)、(b)可见,吹除喷嘴设置在1.7m处比位置处,分离区下游壁面静压比和密度相对更低,可更有效地减小壁面处压力梯度,避免强湍流的产生,湍流边界层对主流的影响减弱,改善了流场环境.由图9(c)可见,喷嘴位于1.7 m处时,分离区后壁面边界层外马赫数最大,且变化平稳,同样图9(d)显示喷嘴位于该处时,分离区下游摩阻系数最小.由此得出:吹除喷嘴设置在1.7 m处时,分离区下游流场最为稳定,改善明显,壁面阻力损失小,吹除控制效果最佳.
2.5 吹除压力效果分析
图10给出了吹除喷嘴设置在X=1.5 m处,总压分别为1.0 P、0.5 P、0.245 P、0.2 P 和0.14 P 时流场波系图,图中总压分别对应吹除喷嘴出口马赫数为2.0、1.54、1、0.83 和0.36.注入吹除气体后,流场波系结构变为复杂.由图10(a)、(b)可以看出,喷嘴斜面产生斜激波与主流斜激波相交,为了匹配交点后流体压力和速度方向,交点后产生两道新激波,一道沿原主流激波方向继续传向壁面,另一道则沿喷嘴处斜激波方向传向下游.传向壁面的斜激波再与喷嘴斜面末端形成的膨胀波相交,转折后传向下壁面边界层,遇到壁面最终形成反射激波,而与之相交的膨胀波转折一定角度后传向下游.图10(c)、(d)和(e)中注入的为亚音速气流,故在喷嘴斜面处不会形成斜激波,注入的气体直接与边界层内气体混合,混合气体速度得到了提高,因此抑制了边界层分离.由图还可发现,喷嘴出口马赫数越接近音速,喷嘴末端形成的膨胀波越明显.

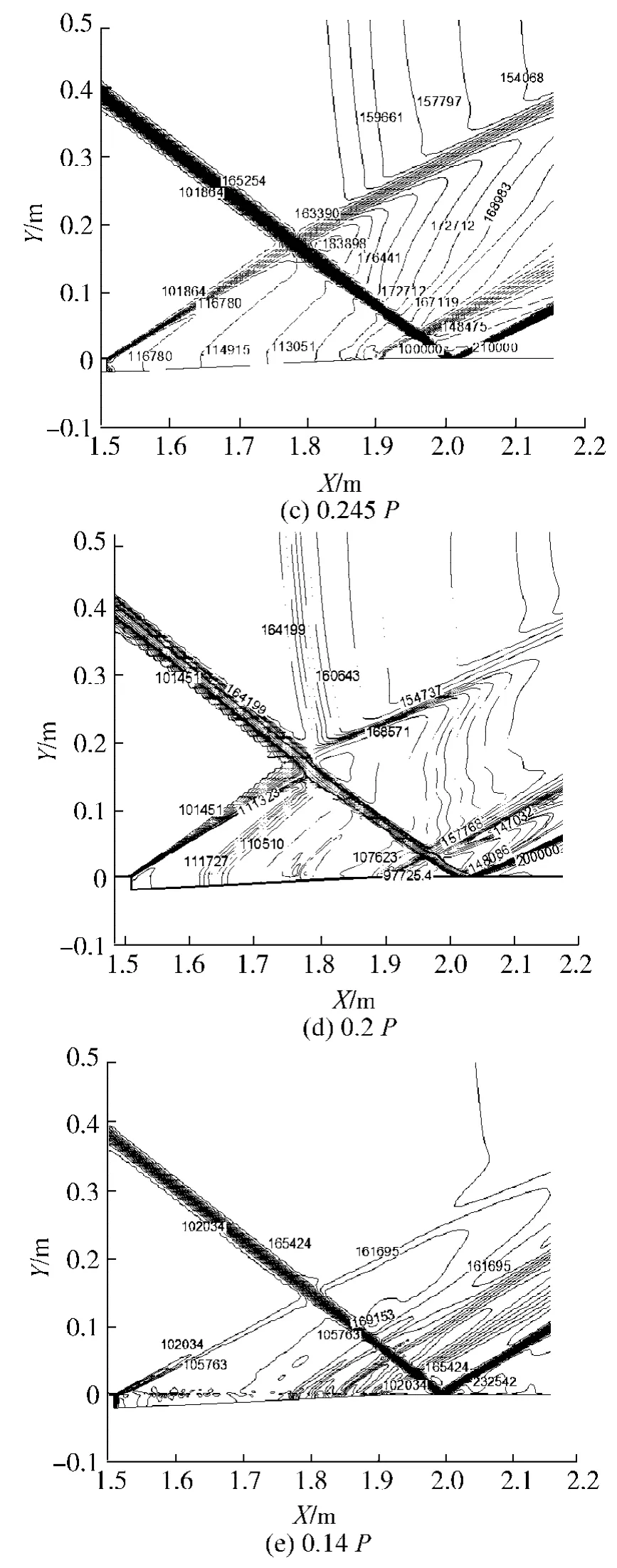
图10 喷嘴位于X=1.5 m处不同总压流场波系结构Fig.10 W ave system of flow field and local am plification
由图11(a)、(b)和(c)可以发现:当喷嘴吹除总压为0.245 P(喷嘴出口Ma=1)时,分离区下游壁面静压比、密度和壁面摩阻系数最小,其次是0.2 P,而0.14 P、0.5 P 和 1.0 P 时各参数相差很小.图11(d)中,吹除总压为0.245 P时,分离区下游壁面边界层马赫数最大,0.2 P次之,0.14 P、0.5 P和1.0 P时相差不大.分析认为吹除总压高于0.245 P时,喷嘴处形成的斜激波损耗了部分吹除能量,使其未得到充分利用,反之低于0.245 P时,喷嘴处为亚音速流动,注入气体直接与下游分离区气体混合,注入气流越接近音速,混合气流速度越高,改善边界层分离效果也越明显.
评价进气道性能优劣主要参数是总压恢复系数及其分布.图12给出WPC模型不同Y截面上总压分布,由图可见Y=0.1m截面上的总压损失最大,说明该截面最靠近边界层,主流斜激波和边界层分离给其带来的损失最大.图13给出了该截面总压恢复,由图13可见,沿X轴方向不同吹除总压下曲线变化趋势相似,X=2m之后总压提高最为显著.其中吹除总压为0.245 P时,总压恢复最高,0.2 P 次之.由图还可看出,虽然吹除总压0.14 P、0.5 P 和1.0 P 之间相差数倍,但吹除效果是相同的,再结合图11、14,可证明并不是吹除总压越高,吹除效果就越好,该结论与R.H.Tindell和B.P.Willis实验结果是一致的,对吹除压力要求的降低,可直接导致对吹除设备要求的降低,这是十分有利的.本文研究发现存在一个最佳吹除压力,该压力就是使吹除喷嘴出口气流达到近似音速.
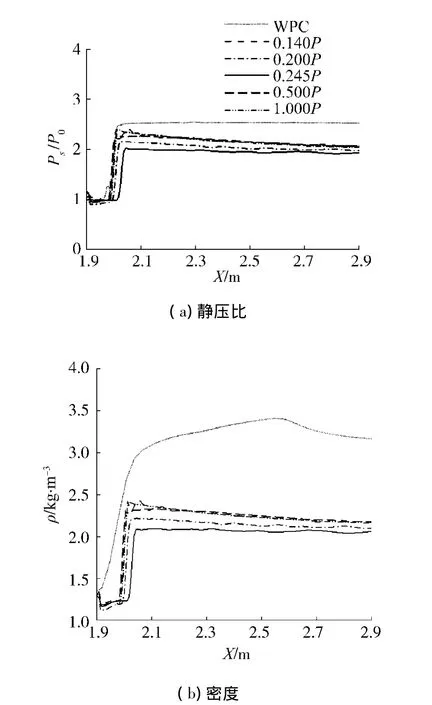
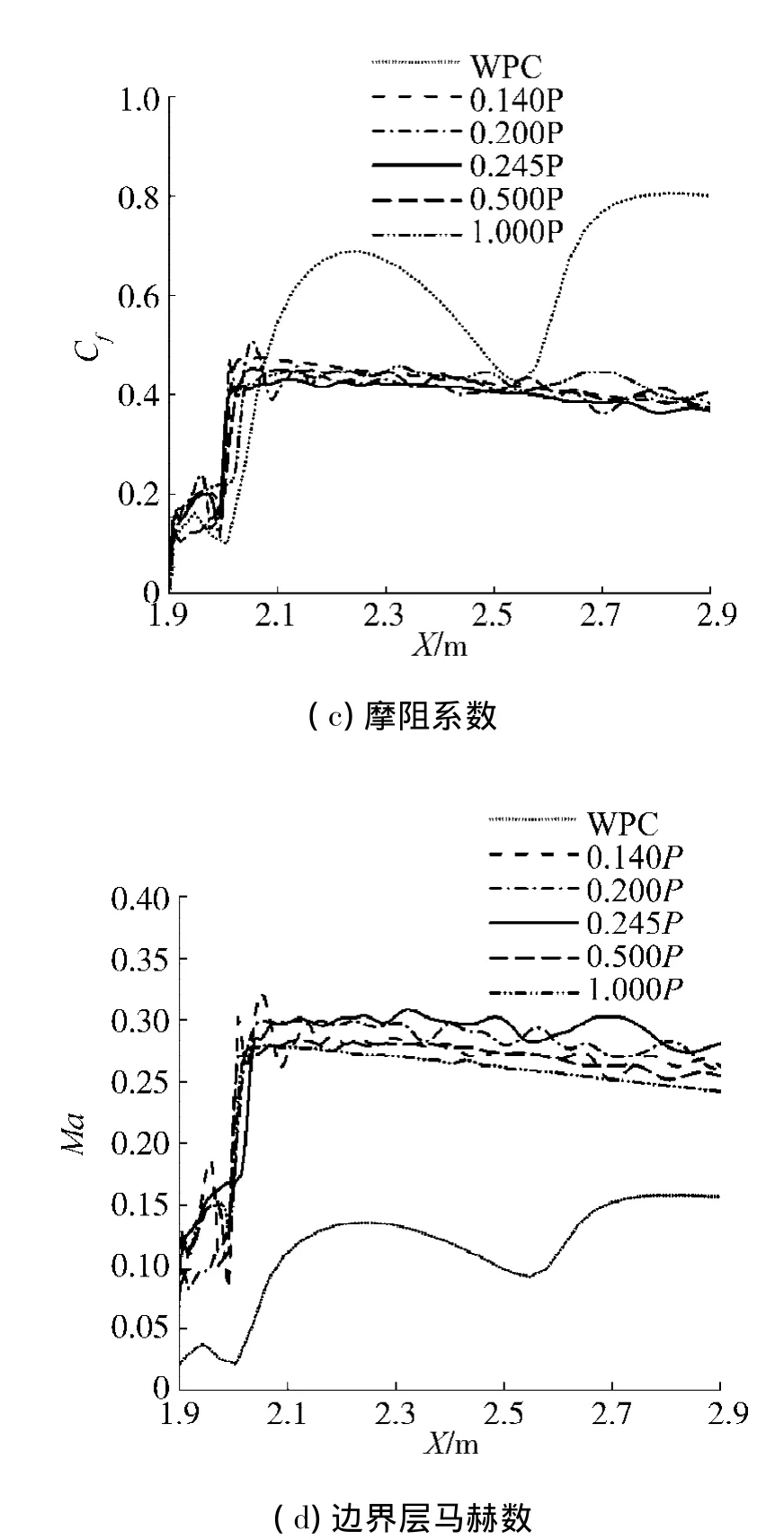
图11 不同吹除总压下壁面参数分布Fig.11 W all parameters distribution of different blow ing total pressure
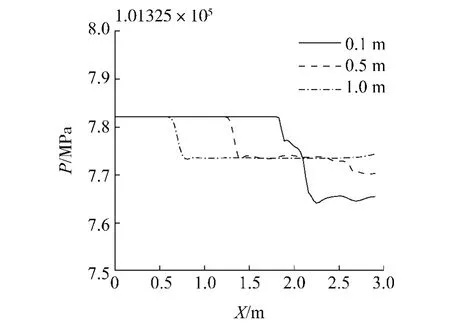
图12 WPC模型不同截面总压Fig.12 Different total pressure distribution in WPC model
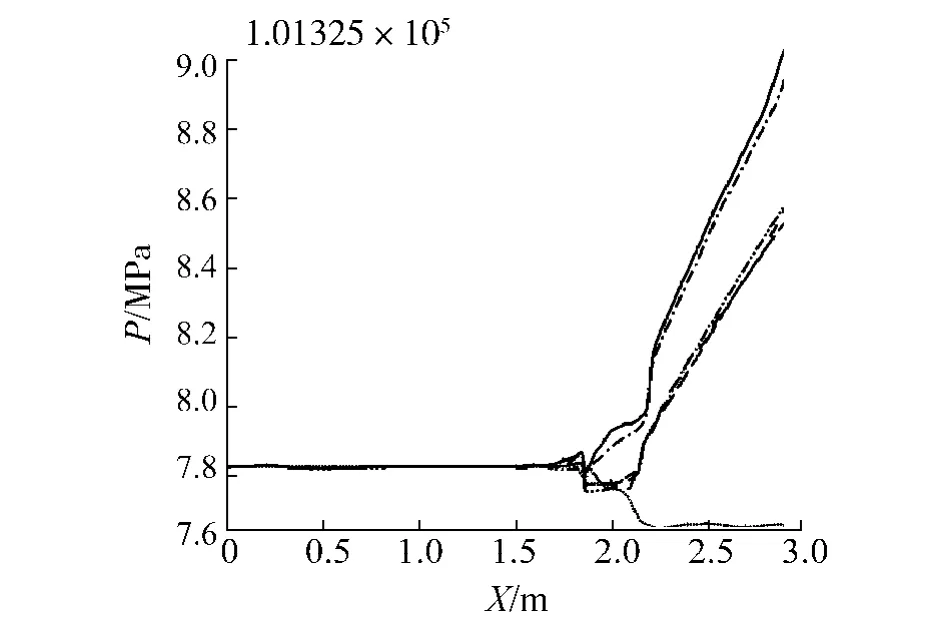
图13 Y=0.1 m截面总压恢复Fig.13 Total pressure in Y=0.1 m
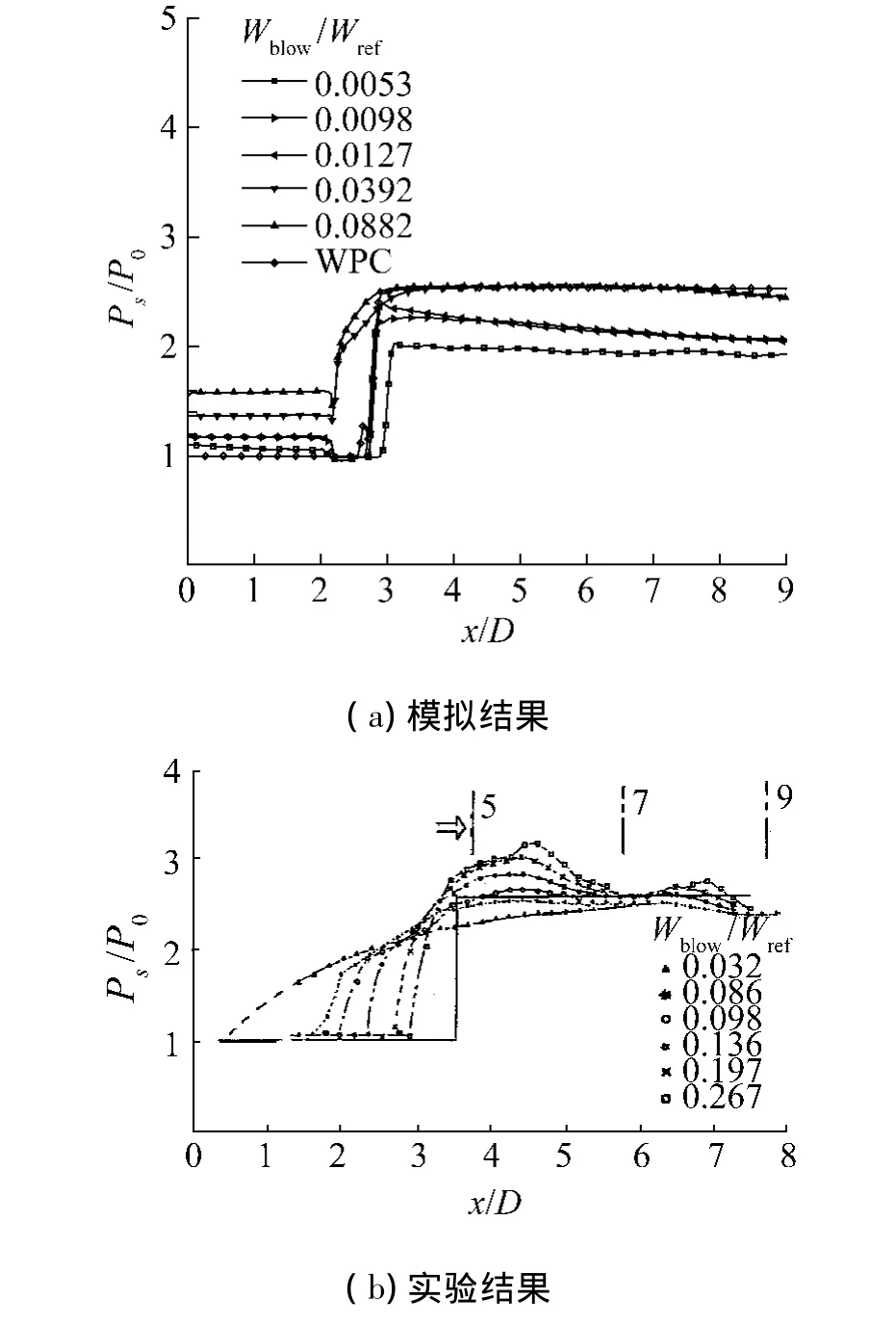
图14 模拟结果与实验结果对比Fig.14 Comparison of simulation and experimental results
3 结论
1)RSM湍流雷诺应力模型模拟进气道激波边界层的干扰及边界层吹除是可行的;
2)下游流场壁面参数的变化和激波强度主要受吹除喷嘴入口总压和位置的影响,吹除喷嘴靠近分离区,吹除效果更好;
3)在加入吹除控制时,流场的波系结构有新的变化,如激波在自由表面、壁面的反射,激波—激波相交、激波—膨胀波—压缩波的相互作用、激波—边界层—膨胀波、压缩波的相互作用等等;
4)吹除总压并不是越高,吹除效果就越好,存在一个最佳吹除压力,该压力就是使吹除喷嘴出口气流达到近似音速.
[1]YOUNG D D,JENKINSS An,MILLER D N.A investigation of active flowfield control for inlet shock/boundary layer interaction[C]//41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference& Exhibit.Tucson,USA,2005:1-11.
[2]张红军,忻贤钧,白葵,等.超声速进气道边界层吸除方案设计及实验[J].实验流体力学,2008,3(22):88-91.ZHANG Hongjun,XIN Xianjun,BAIKui,et al.Design and wind tunnel test on supersonic inlet with boundary layer bleed[J].Journal of Experiments in Fluid Mechanics,2008,3(22):88-91.
[3]BUR R,BENAY R,CORBEL B,et al.Physical study of shock wave/boundary-layer interaction control in transonic flow[C]//38th AIAA Aerospace Sciences Meeting& Exhibit.Reno,Nevada,2000:1-11.
[4]LIN Y L,RIMLINGER M J,SHIH T L,et al.Control of shock/boundary-layer interactions with passive blowing and bleeding[C]//33st AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit.Seattle,WA,1997:1-9.
[5]HEALY M,O'ROURKE M J,RAGHUNATHAN SR.Further investigations of passive vortex control jets for shock boundary layer interactions[C]//1st AIAA Flow Control Conference St Louis,Missouri,2002:1-11.
[6]HAFENRICHTER E,LEE Y,MCLLWAINS T,et al.Experiments on normal shock/boundary layer interaction control using pyroclastic mesoflaps[C]//39th AIAA Aerospace Sciences Meeting & Exhibit.Reno,Nevada,2001:1-13.
[7]HOLDEN H,BABINSKY H.Shock/boundary layer interaction control using 3D devices[C]//41th AIAA Aerospace Sciences Meeting & Exhibit.Reno,Nevada,2003:1-8.
[8]SRINIVASAN K,LOTH E,DUTTON J.Aerodynamics of recirculating flow control devices for normal shock/boundary layer interactions[C]//42th AIAA Aerospace Sciences Meeting & Exhibit.Reno,Nevada,2004:1-22.
[9]TINDELL R,WILLIS B.Experimental investigation of blowing for controlling oblique shock/boundary layer interactions[J].AIAA,1997(2642):498-516.
[10]闫超,陈靓.激波/边界层干扰数值模拟的格式效应[J].航空学报,1996,17(9):67-70.YAN Chao,CHEN Liang.The scheme effects of numerical solutions for shock boundary layer interaction[J].Journal of Aeronautics,1996,17(9):67-70.
[11]HAKKINEN R J,GREBER I,TRILLING L.The interaction of an oblique shock wave with a laminar boundary layer.2-18-59w[R].NASA,MeMo,1959.

