磁电弹性耦合材料中的本构关系

曲 磊， 王建国， 钱 锋

（合肥工业大学 土木与水利工程学院，安徽 合肥 230009）

磁电弹性耦合材料具有同时感知磁、电、力影响的能力，因其具有独特的机电和磁力转换能力，这种材料（如压电、压磁和磁电弹性材料）和结构已被大量应用于传感和制动控制、信息处理以及材料科学等领域。在磁电弹性材料中，磁场、电场和力场具有相互转换的作用，例如磁电弹性体被放置于电场中将被磁化，将其放置于磁场中会电极化，而将其置于磁场或者电场中也会有应变产生。文献［1－2］介绍了多种压电／磁致伸缩材料所表现的磁电耦合现象，这些材料被称为磁电弹性耦合材料；对于磁电弹性材料力、电、磁的耦合行为研究，文献［3］最早指出将压电－压磁材料进行组合，将产生一种新材料的特性，它不仅具备原有的压电材料和压磁材料的特性，并且具有非常显著的磁电耦合性能；文献［4－5］从理论上提出了压电、压磁材料的细观力学模型来估算其耦合效应；文献［6］利用均匀场的概念得到了在纤维状压电、压磁弹性耦合效应中不同部分之间的精确关系；文献［7－8］通过引入传递矩阵的方法，推导了横观同性三维简支磁电弹性板静力问题的精确解；文献［9］运用状态空间的方法分析了由压电和压磁材料组成的复合结构磁电耦合影响；文献［10］推导了层状压电、压磁介质轴对称问题的状态空间解。

1 磁电弹性体8种形式本构方程的推导

磁电复合材料的磁电效应来源于磁致伸缩效应与压电效应的乘积。由于磁电转化效应是磁、电、力多场耦合的结果，为了有效地设计复合材料的组分与结构，需建立磁电复合材料磁电转化效应的理论分析模型。磁电弹性体的耦合作用是通过磁、电、力的本构关系反应的，文献［11－12］给出了压电材料4种形式和压磁材料4种形式的本构关系。本文在前人研究的基础上，通过假设不同的独立变量扩展了磁电弹性体本构关系的多种形式。

1.1 第1种形式的本构方程

根据连续介质热力学理论，引入绝对恒温条件下的磁电弹性体热电磁Gibbs自由能状态方程U1，即

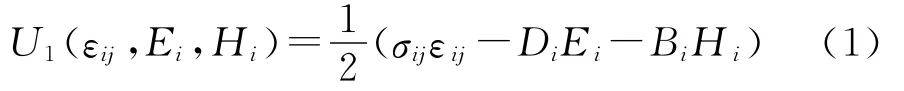
其中，U1为磁电弹性体介质的能量密度；σij、εij分别为应力和应变；Di、Ei分别为电场强度和电位移；Bi、Hi分别为磁场强度和磁势。

因为U1是εij、Ei和Hi的二次函数，则U1可以展开成：

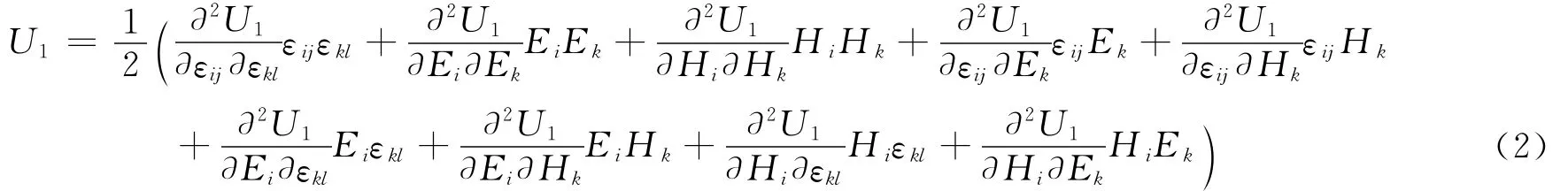
由方程（1）可得：

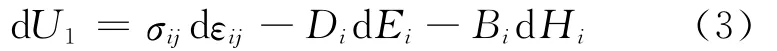
由于U1为εij、Ei和Hi的二次函数，根据Gibbs自由能理论，dU1又可以写成：

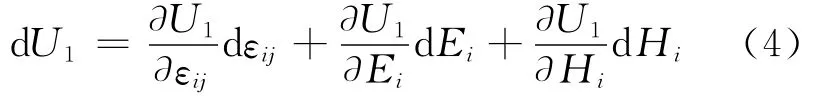
比较方程（3）和（4）得：

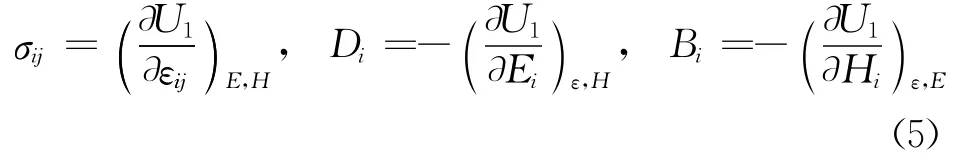
利用方程（2）和（5）得：

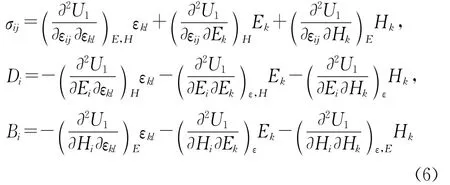
通过引入常数：

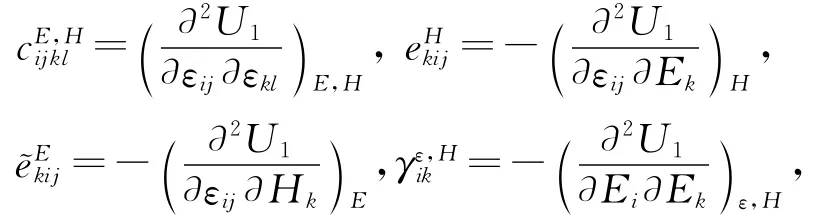
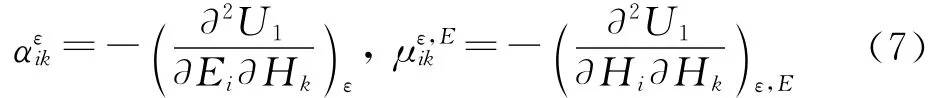
将方程（7）代入方程（6），可以得到第1种形式的本构方程为：

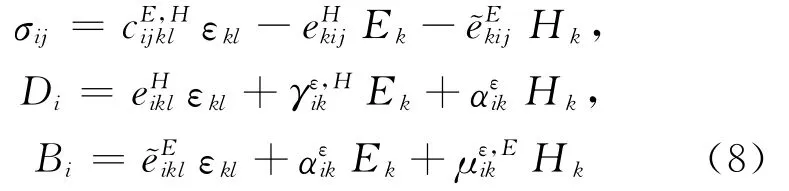
方程（8）即为第1种形式的本构方程，它将应变εkl、电势Ek和磁势Hk作为独立的变量，该形式的本构方程是目前磁电弹性体中普遍使用的一种形式，已有的大部分研究成果都是基于此种形式。本文将通过假设不同的参数作为独立变量，从而推导出磁电弹性体另外7种形式的本构关系，具体推导过程如下。

1.2 第2种形式的本构方程

对U1（εij，Di，Hi）进行Legendre变换后可得：

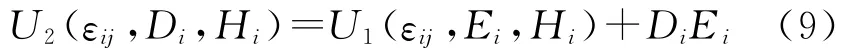
由方程（1）和（9）得：

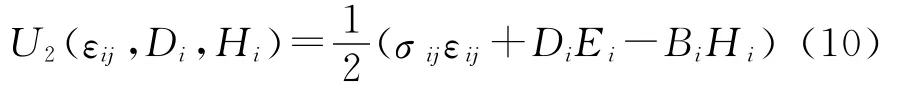
U2为εij、Di和Hi的二次函数，U2可以展开为：

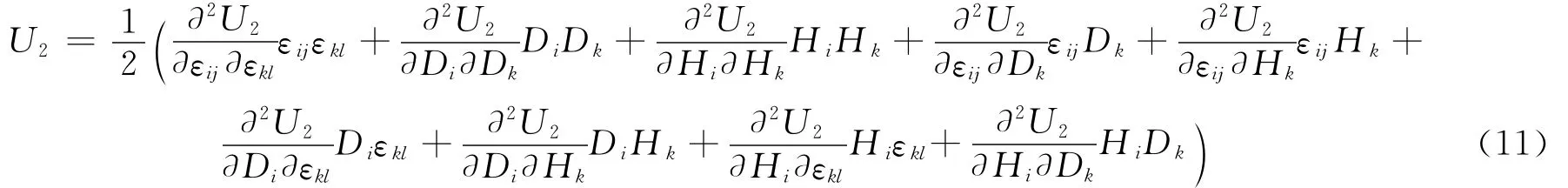
由方程（10）可得：

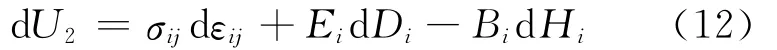
由于U2为εij、Di和Hi的二次函数，根据Gibbs自由能理论，dU2又可以写成：

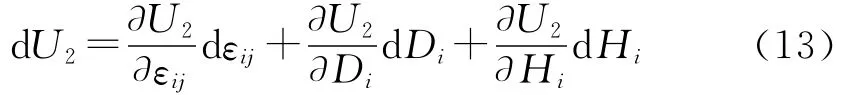
比较方程（12）和（13）得：

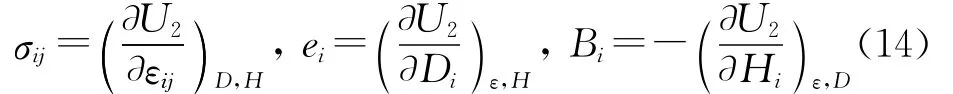
利用方程（11）和（14）得：

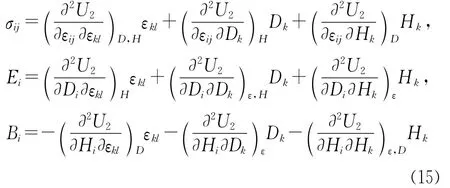
通过引入常数：

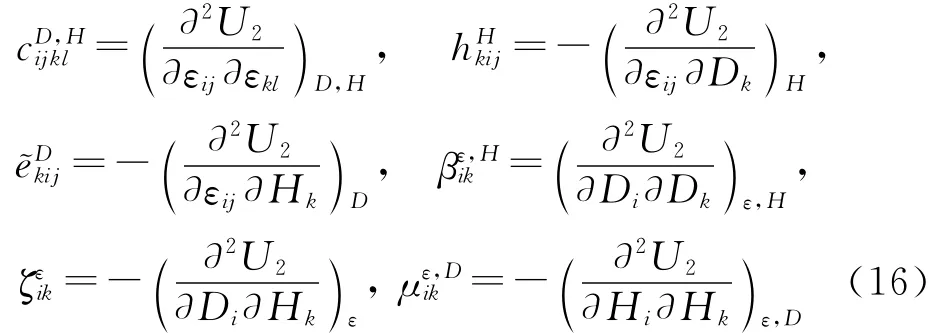
将方程（16）代入方程（15），得到第2种形式的本构方程为：

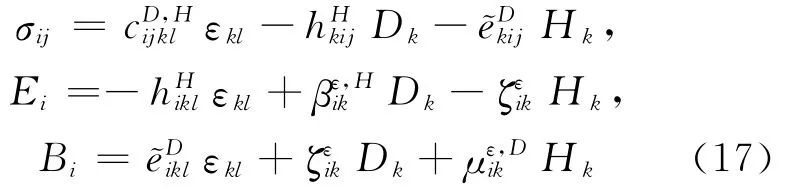
1.3 第3种形式的本构方程

对U1（εij，Di，Hi）进行Legendre变换得：

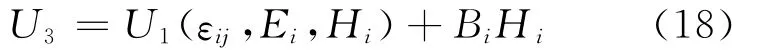
由方程（1）和（18）得：

U3为 εij、Di和 Hi的 二 次 函 数。U3可 以展开成：

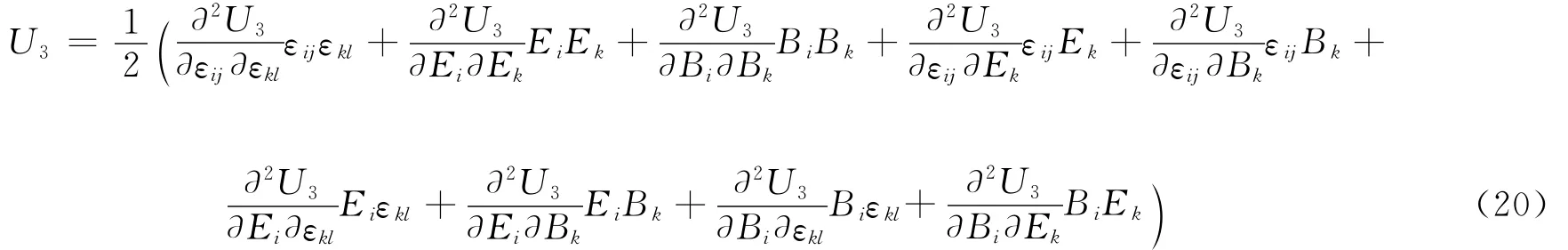
由方程（19）可得：

由于U3为εij、Di和Hi的二次函数，根据Gibbs自由能理论，dU3又可以写成：

比较方程（21）和（22）得：

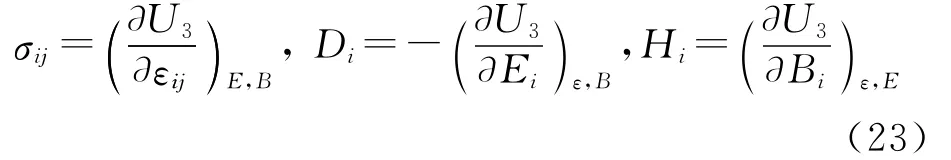
利用方程（20）和（23）得：

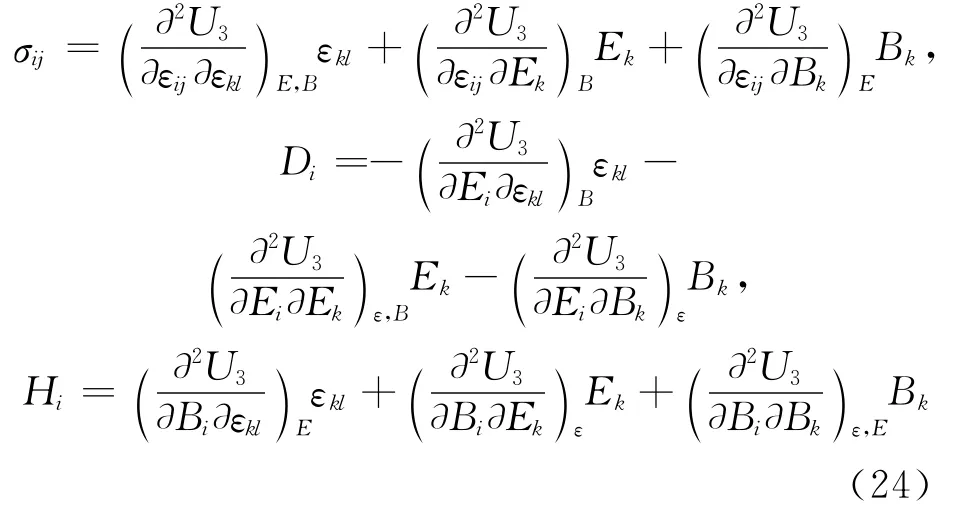
引入如下常数：

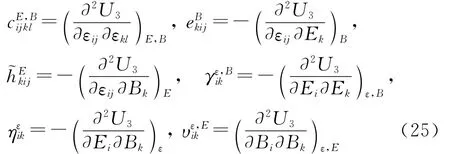
将方程（25）代入方程（24），得到第3种形式的本构方程为：

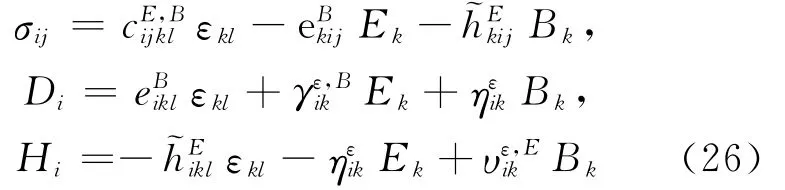
1.4 其他5种形式的本构方程

对于后5种形式的本构方程，因为推导过程类似，本文不一一列出，仅给出推导的结果。

1.4.1 第4种形式本构方程

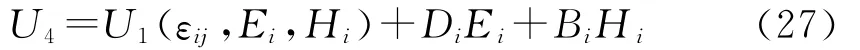
由方程（1）和方程（27）得：

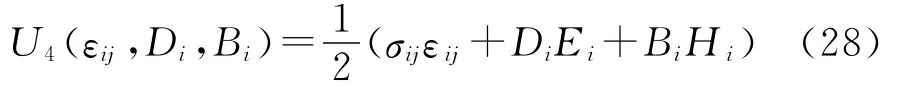
U4为εij、Di和Bi的二次函数，与U4对应的本构关系为：

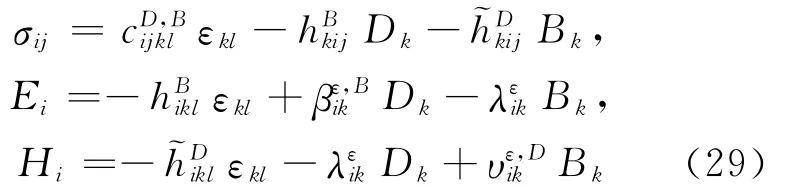
1.4.2 第5种形式本构方程

由方程（1）和（30）得：

U5为σij、Di和Bi的二次函数，与U5对应的本构关系为：

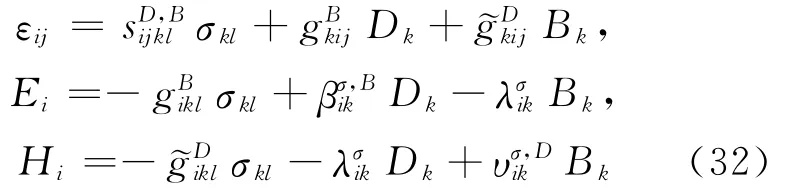
1.4.3 第6种形式本构方程

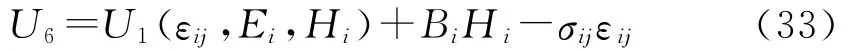
由方程（1）和（33）得：

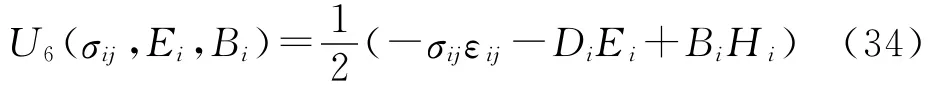
U6为σij、Di和Bi的二次函数，与U6对应的本构关系为：

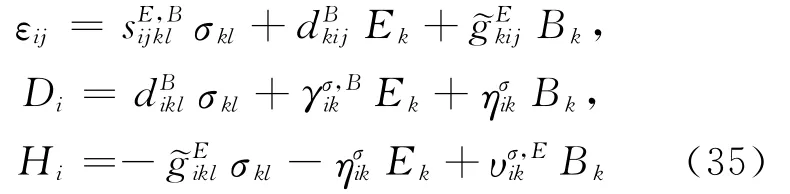
1.4.4 第7种形式本构方程

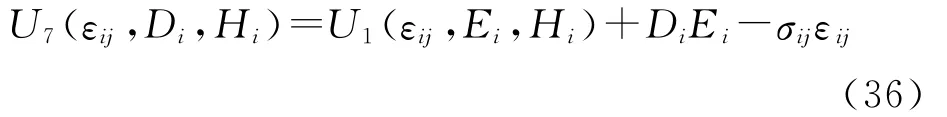
由方程（1）和（36）得：

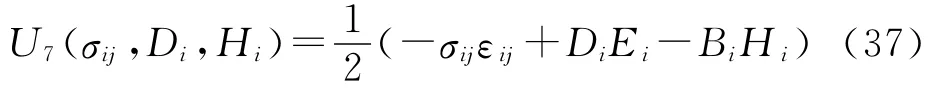
U7为σij、Di和Bi二次函数，与U7对应的本构关系为：

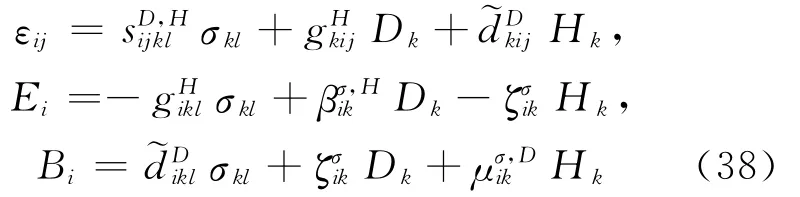
1

.4.5 第8种形式本构方程

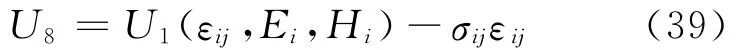
由方程（1）和（39）得：

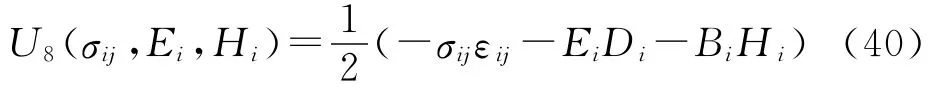
U8为σij、Ei和Bi二次函数，与U8对应的本构关系为：

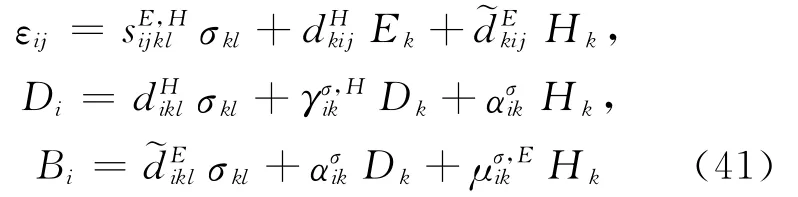
方程（8）、（17）、（26）、（29）、（32）、（35）、（38）、（41）即为所推导出的8种形式的本构方程。

2 结束语

本文考虑磁电弹性复合材料磁电耦合性能的影响，根据连续介质的热力学理论，通过引入Gibbs自由能和Legendre变换推导了磁电弹性耦合材料8种形式的本构方程，据此可建立不同形式的变分原理。本文所得的研究成果为磁电弹性耦合材料的有限元方法的研究提供了理论基础。

［1］ Ryu J，Priya S，Uchino K，et al.Magnetoelectric effect in composites of magnetostrictive and piezoelectric materials［J］.J Electroceram 2002，8：107－119.

［2］ Fiebig M.Revival of the magnetoelectric effect［J］.J Phys D：Appl Phys，2005，38：123－152.

［3］ Van Run A M J G，Terrell D R，Scholing J H.An in site grown eutectic magnetoelectric composite material：part 2，physical properties［J］.J Mater Sci，1974（9）：1710－1714.

［4］ Nan Cewen.Magnetoelectric effect in piezoelectric and piezomagnetic phases［J］.Phys Rev B，1994，50：6082－6088.

［5］ Huang J H，Kuo W S.The analysis of piezoelectric／piezomagnetic composites materials containing ellipsoidal inclusions［J］.J Appl Phys，1997，81：4889－4898.

［6］ Benveniste Y.Magnetoelectric effect in fibrous composites with piezoelectric and piezomagnetic phases［J］.Phys Rev B，1995，51（22）：16424－16427.

［7］ Pan E.Exact solution for simply supported and multilayered magneto－electro－elastic plates［J］.Journal of Applied Mechanics，2001，68：608－618.

［8］ Pan E，Heyliger P R.Free vibrations of simply supported and multilayered magneto－electro－elastic plates［J］.Journal of Sound and Vibration，2002，252：429－442.

［9］ Wang J G，Chen L F，Fang S S.State vector approach to analysis of multilayered magneto－electro－elastic plates［J］.International Journal of Solids and Structures，2003，40：1669－1680.

［10］ 关 群.层状压电、压磁介质轴对称问题的状态空间解［J］.合肥工业大学学报：自然科学版，2003，26（1）：117－122.

［11］ ANSI／IEEE Standard 176－1987，IEEE standard on piezoelectricity［S］.

［12］ ANSI／IEEE Standard 319－1990，IEEE standard on magnetostrictive materials：piezomagnetic nomenclature［S］.