基于水下光电成像系统研究计算机仿真技术

黄煜栋，李利正，沈华峰

（绍兴职业技术学院，浙江 绍兴 312000）

0 引 言

水下光电成像探测系统运用的范围越来越广泛，在系统设置、后续图像处理算法分析、水下图像识别等方面，水下光电成像探测系统均能起到一定的指导作用，海水光学特性以及测量也能够因此受到启示[1-2]。Jaffe研究了水下环境中经过一定的环节之后得到像理所包含的性能极限现象。本文正是基于Jaffe所构建的关于小角度近似原理的理论模型，深入对水下光电成像系统中所存在的量化演算机制进行研究，构建仿真流程。

1 信号辐射演算模型

1.1 接受系统的信号分类

从前人已经构建的关于水下光电成像系统模型的内在机制来看，其模型已经具有了全过程的特征，即动态地反映了光线从发射系统射出一直到达其接收的流程[3-5]。其运作机制如图1所示。

从图1可知，当光线从光源发出到其被接收的过程，一共出现了3种不同的光线发射方式，即直接传输、前向散射以及后向散射。以ET来表示在成像系统下所接收的总辐射光通量，用Ed表示直接传输，Efs表示前向散射，Ebs表示后向散射，那么这些量之间的关系式[6]可以表示为

图1 水下光电成像探测系统光线示意图

1.2 构建系统结构模型

发射对象物与接收系统之间的距离，是构建成像体系的关键性因素。其具体示意图如图2所示。

图2 水下成像系统结构模型示意图

用参量d表示发射对象物与接收系统之间的距离，Rm表示相距接收体系的距离，Wm表示在相距Rm的地方且在接收系统全视场环境下物面宽度数值的参量，Hm表示物面的高度数值参量，用围绕着物面核心点O（Wm/2，Hm/2）的地方来表示相应的视场坐标原点，用（θR，φR）来表示任一点（m，n）所代表的极限分辨单位角坐标，且用（H，W）来表示相关的直角坐标。引入参量δ来表示在物面方位之内标准像素距离，关系式为

由于物面和接收系统之间形成了一个自足的空间，在该空间内可以自由地展开辐射传播，在成像主光线路径上任意选择一坐标（m，n），其与接收系统OR之间距离为Ra，那么该空间坐标可以表示为（OR，φR，Ra），其与发射对象物 Oi的相对空间极坐标为（θl，φl，Rl），具体的数值可以通过式（3）来加以量化。

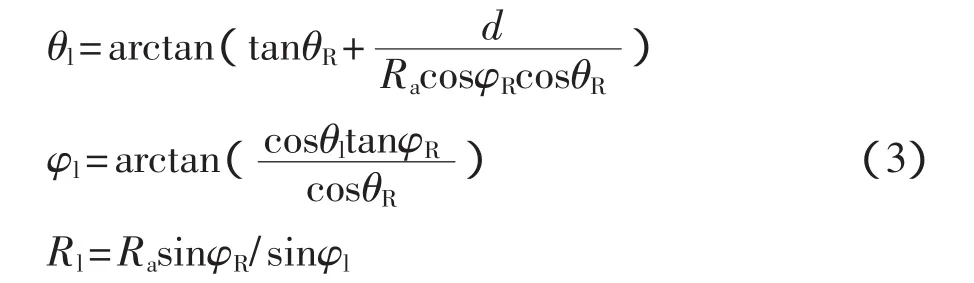
1.3 对信号以及前向散射辐射量展开的量化研究

光线发射于物面的强度情况在研究景物面反射量的过程中，具有十分重要的作用；因此，要对其进行一定的量化研究。例如任意在物面上选择一点s（m，n），且其与发射体系Ol之间的极坐标表示为（θs，φs，Rs），那么当光线顺着主轴Rm发出的时候，产生的光强表示为Ⅰ，而物面s（m，n）轴向上的辐射强度表示成Ⅰ（θs，φs）。由于存在着衰减效应与分散效应，因此，参量关系式为

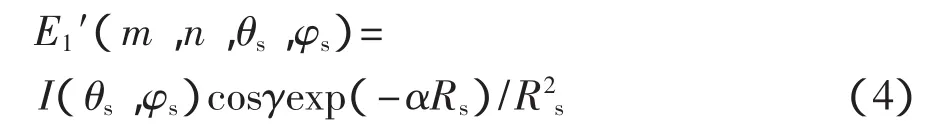
式中：γ——发射体系Ol和s（m，n）之间的连线以及经由物面s（m，n）垂直方向上连线的夹角参量，并得到Rs与γ的关系式为

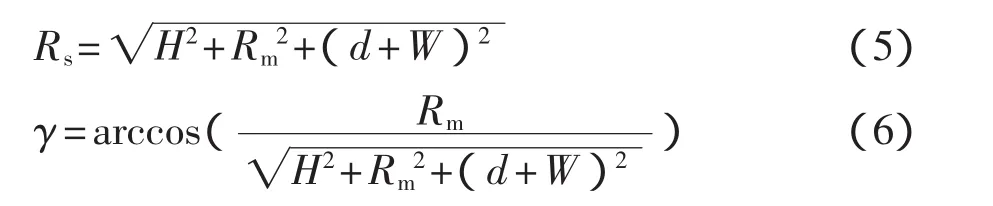
在反射的物理过程中，s（m，n）则可以被认为是初始点。用E1（m，n，o）来表示光线入射过程中的光通量大小，则有：

光线在入射的过程中的光通量需要达到更为精确的程度，而在前向散射过程中会出现小角度的变化情况；因此，在这个情况下，需要额外地借助于点扩散函数g来加以说明：

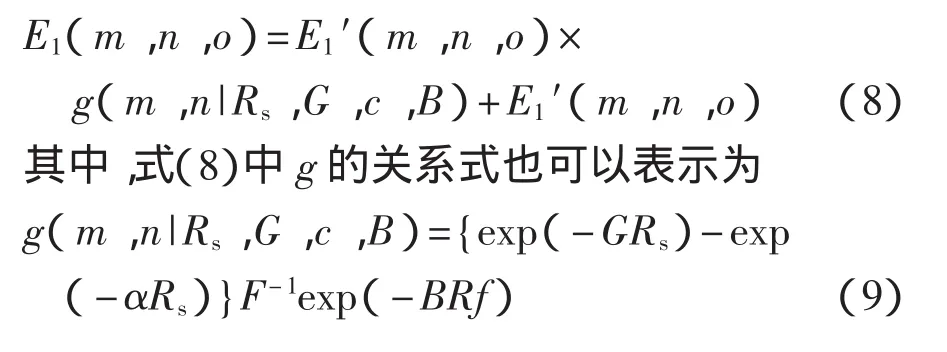
式中：G——常量，且|G|≤α；

B——衰减因素常量；

f——空间频率常量。

接下来对反射辐射进行量化分析。从数值上看，它是入射辐射的数值与s（m，n）反射率ρ的乘积。且大多数情况下，ρ≤1；在通常海洋环境中，ρ∈[0.02，0.1]。依据朗伯定律，倘若用θ表示出射光线与点s（m，n）的连线以及经由该点且垂直于物面直线的夹角变量，那么应该借助于cosθ的媒介作用。依据光学体系中关于孔径以及反射波等原理，可以得出如下的关系式：

其中，式（10）中的f#表示接收F参量的数目，且Tl表示透镜率数值的大小。其关系式为

考虑到直接辐射量以及点扩散函数g等参量，可以得到关系式为

1.4 后向散射辐射量

后向散射在被接收的过程中，具有大角度范围的特点，将三维空间进行肢解是最为常用的方法。三维空间经过肢解之后，得到了若干个像面厚度为ΔZi的子平面，同时，这些子平面与接收体系形成平行的关系。

首先对射入这些子平面的辐射量展开量化的计算，最为关键的是直接辐射以及由于小角度的存在而造成的散射与附加辐射数值。其次，研究入射光在分割切片的影响下所出现的后向散射现象及其最终辐射量的数值大小。在这个过程中，通常用Es（x′，y′，z′）来表示光线经由发射体系到达三维空间后入射光的通量大小。研究表明，进入到体积元的入射光量与直接投射、前向散射之间存在着如下的关系式：

根据散射原理，在切片媒介的作用下，一些入射光经过散射之后，能够进入到接收体系的数据径路，同时，其数值则取决于介质的内在特性体积散射函数（通常用β（φ）来表示）关系。用ΔV′来表示三维水域中的一个递增的体积参量，用（x，y）来表示入射光所遭受到的接收体系的单元参量，用φbs来表示线（即连接体积元与光源）与线（即连接体积元与接收体系）之间的夹角参量，用Hbs来表示在这样的情境下的辐射强度，那么，相应的关系式则可以表示为

式（17）中的β（φbs）表示入射光在经由入射点（θl，φl）出发在介质的作用下发生散射之后，突转到（θR，φR）闯入数据径路的程度大小。

完成上述的步骤之后，再对后向散射的数据展开研究。用ΔRai表示后向散射体积ΔV′厚度的参量，用Rai表示接收体系中任一选取的像素点与水体切片核心点之间的相距参量，用N来表示切片的数量参量，用Ebs，d（m，n）表示后向散射的直接部分参量，用Ebs（m，n）表示在由于后向散射所造成的总辐射量的参量。关系式为

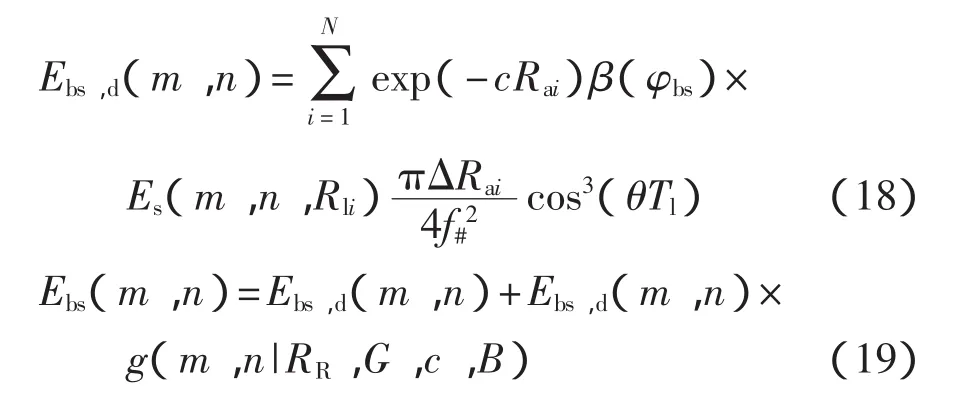
2 计算机仿真技术分析

2.1 基于对比度的计算原理解析

由于背向和前向散射正好是两个相反的关系，这二者之间在成像上将会出现鲜明的对比倾向，这在于相近的两个基本单元之间的表现更为明显。以C0来表示最初的对比度参量，那么关系式为

由于后向散射和前向散射效应，成像辐射效果也因此而得到了一定程度的强化；同时，成像比照度呈现出弱化的趋势。其关系式为

其中，式（21）中的 β=（1+γ）-1。同时，由于前向与背向散射的存在，也会出现成像比照度弱减的趋势，其参量可以用γ表示，关系式为

由于比照度数值大小深受散射的影响；因此，需要借助于参量C（m，n）来表示其相关的比照度透过率。从数值上看，其与直接光分量、总光通量之间的关系为

2.2 信号光计算流程

（1）用参量Rm来表示接收体系与探测对象之间的垂直间距。接收体系探测器的单元像素大小被设定为dx×dy，用参量f来表示光学系统的焦距，用δ来表示物面处的标准像素距离的参量，用H来表示物面第（m，n）个探测单元的的位置参量，其关系式为

（2）在式（5）、式（6）的关系式下，得到关于 Rx以及γ的数值。再根据式（5）的关系式，可以得到关于到达物面单元（m，n）光通量的数值。

（3）经由式（7）、式（8）的作用下，得到入射光通量分布的数据。

（4）根据式（10）、式（11）以及式（12），可以得到关于接收体系的信号光通量状态。

2.3 后向散射光演算过程

如图2所示，在展开本节的研究过程中，研究的核心集中于光主轴向度。也就是说，研究的区域被划定为连接物面单元点（m，n）以及接收体系OR二者的范围。当然，在现实运用中，存在着其他方向上散射光的影响。具体展开的途径如下：

（1）在上述多划定的区域之内进行细致的M等分，并对其顺序编号。其方向以趋靠于物面单元点（m，n）的范围之内为起点，在上述相关的式（2）、式（3）与（4）的关系式之下，演算出各个范围之内的角坐标数值大小。

（2）从发射体系出射光线中找出偏角最大的光线，同时，将物面单元点（m，n）以及接收体系OR二者进行连接，确定此连线与前面的光线的交点，进而得出相关散射的最大区域编号，并用N来表示。

（3）在若干个体积相位函数模型中选出其一，在式（13）～（18）中，对该范围内经过散射物理环节之后，其在像面的光通量数值大小。

2.4 研究介质的相位函数

在展开后向散射光相关数据的研究过程中，不能忽略相位函数的重要作用。

所谓的“相位函数”，即是对入射光在单个散射介质的作用下所发生散射现象的量化研究工具。从当前的研究情况来看，其数目并不少，最为常用的则是具有单个单参数函数的 Hengey·Greenstein（OTHG）相位函数，具有较为方便实用的优点。用ρ来表示前向散射的参量，其关系式为

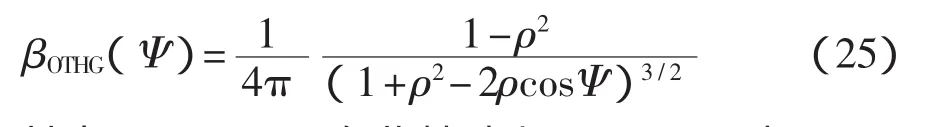
其中，ρ∈[0，1]。在此基础上，用（θl，φl）以及（θR，φR）来分别表示入射与出射光线的方向，又可以进一步得到如下的关系式：

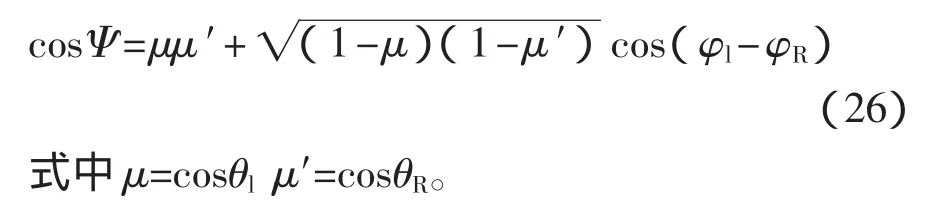
2.5 计算机仿真技术研究

仿真技术的研究是常规状态下借助于激光对水下的成像系统展开研究，其研究的核心内容为激光发射系统、接收系统二者之间的间距以及对比度的关联性。

为方便研究以及计算，认为光源系统以及接收系统处于平行的关系，并理想化地认为发射各个方向的光线强度等同。在仿真技术体系环境之下，前向散射系数的数值是0.5，其仿真效果如图3所示。

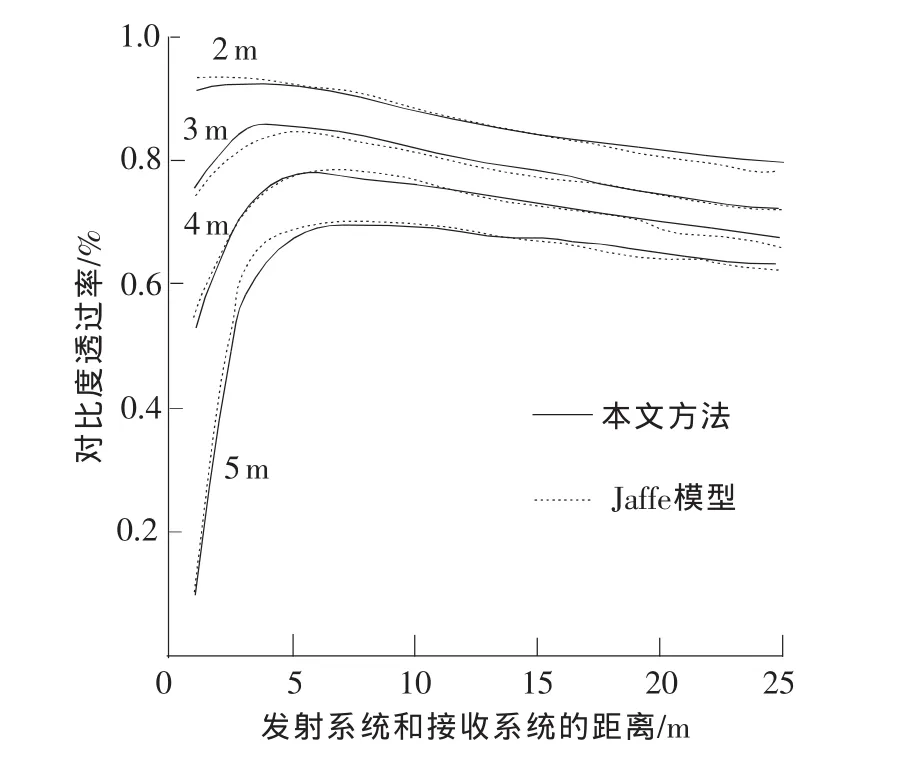
图3 基于对比度透过率以及发射、接收系统距离的关联性对比本文研究方法以及Jaffe模型的仿真效果图

通过相关的数据研究表明，本文研究方法与Jaffe模型的研究方法效果相近；在一定范围之内，光源系统以及接收系统的距离与散射光（尤其是后向散射光）效果之间存在着负相关的关系，即后者随着前者的增大而降低，水下成像功能则越好。从科学物理的角度而言，这二者之间的距离增大，入射角以及散射角也相应地递增，散射效应则反向递减。此外，激光主轴处于朝向探测物面的方向，信号光基本上保持原状。

3 结束语

本文在相关小角度散射的原理下，研究水下激光成像物理流程并构建相应的模型。由于散射光的存在，系统化地研究了距离处于既定状态下，水下成像面各因素的信号辐射量，并以量化的方式进行研究，建构具有对比度性的理论模型。同时，也从现实应用的角度出发，对常见的激光助视水下成像系统技术展开了仿真的研究，重点分析了光源系统以及接收系统的之间的距离以及成像对比度的关联性问题。

[1]徐放阳，杨坤涛，王新兵，等.蓝绿激光雷达海洋探测[M].北京：国防工业出版社，2002.

[2]张毅，柏连发，陈钱，等.布里渊散射在水下激光成像探测中的应用[J].红外与激光工程，2009，38（4）：665-668.

[3]黄有为，金伟其，丁琨，等.基于光束空间展宽的水下前向散射成像模型[J].红外与激光工程，2009，38（4）：669-673.

[4]孔捷，张保民.水下光电成像系统计算机仿真[J].南京理工大学学报：自然科学版，2010（3）：78-80.

[5]李丽，高稚允，王霞，等.水下距离选通成像系统后向散射光的计算[J].北京理工大学学报，2003（4）：81-84.

[6]孔捷，张保民.激光水下成像技术及其发展[J].光电子技术，2006（2）：80-90.