平面二次包络四轴四联动数控磨床加工原理及实验研究*

韩兴国 黎亚元 和法洋

（①桂林航天工业高等专科学校，广西桂林541004;②西华大学数控技术研究所，四川成都610039;③上海合众重工有限公司，上海 201506）

平面二次包络蜗杆传动是我国在20世纪70年代研制的一种新型的机械传动方式，具有效率高、寿命长、承载能力强等特点，特别适用于现代机械重载、高速的要求，产品深受客户欢迎［1］。但由于这种蜗杆加工工艺非常复杂、设备专用、价格昂贵，所以应用推广受到较大限制。为了克服这些问题，我们通过深入研究，提出了一种利用数控圆插补运动加上砂轮架自转运动以及被磨削蜗杆的轴旋转运动的新加工工艺，并在此基础上开发了四轴四联动的数控磨床。该磨床克服了原来存在的问题，使加工的蜗杆的中心距可在很大的范围内变化，而且机床结构紧凑，节省了空间、提高了效率。该磨床已投入到生产实践中，经验证符合加工要求。

1 加工原理

平面二次包络四轴四联动数控磨床的工作原理如图1所示，X向和Z向双层工作台上安装了可绕自身旋转的砂轮回转台，上面安装了磨削头。X、Z轴联动实现圆插补，带动砂轮回转台和磨削头作轨迹为圆的平移运动，与此同时如让砂轮回转台带动磨削头按一定规律绕回转中心O2的作B轴旋转运动，实现X、Z、B三轴联动即可保证砂轮的产形面始终与基圆相切。它们与蜗杆的主回转运动C合成即实现四轴联动，可实现蜗杆与蜗轮的啮合运动完成整个加工。通过分析论证，这种加工工艺完全符合平面二次包络蜗杆的磨削加工原理［2］。

2 运动分析

以加工工件的位置为基准，插补圆的圆心由工件蜗杆副的中心距a决定，在工件喉颈圆弧中心线上，它也是蜗轮的基圆圆心，这个插补圆心可以通过数控编程实现，所以非常灵活也很容易实现。这样就不必为了制造大中心距的蜗杆而制造大型的磨床，大大简化了磨床结构，调整也比较方便。

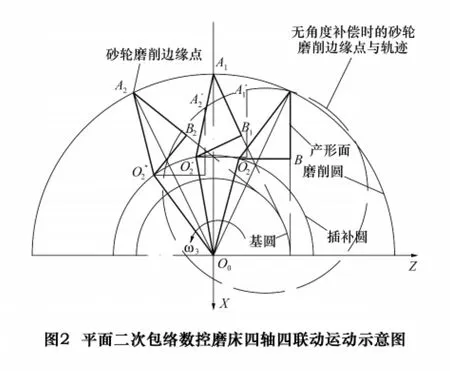
如图2所示，O0为插补圆、基圆、理想磨削圆的圆心，O2为砂轮回转台的回转中心，AB为砂轮产形面，A表示加工蜗杆的砂轮产形面上的磨削边缘点。X、Z作逆圆插补时，砂轮回转台回转中心由O2→O'2→O″2。若是没有添加回转台自身的回转运动B，砂轮磨削边缘点移动的轨迹就是图中的A→A'1→A'2，很明显可以看出这时磨削边缘点的位置超出了磨削圆的轨迹，与基圆不同心。要使产形面与基圆相切，必须把磨削头绕中心O2转一角度进行补偿。若添加了回转运动，磨削边缘点的位置由A→A1→A2，其运动轨迹就是要求的磨削圆。且AB、A1B1、A2B2的延长线均与基圆相切，满足了环面蜗杆的啮合原理。

对于不同型号的环面蜗杆，在加工前已经确定了基圆半径rb、蜗杆的齿顶圆弧半径Ra1和齿根圆弧半径Rf1。磨削半径AO0的大小介于齿顶圆弧半径和齿根圆弧半径之间。磨削边缘点A的坐标，在对刀时确定，AB、O2B的大小在机床设计阶段已经确定了。

如图3所示，AB为砂轮磨削的初始位置，与基圆相切。砂轮随着双层工作台的插补运动，延插补圆转过一角度θ3，平动到ΔO'2A'1B'1位置，为使磨削边缘点A1'位于理想的磨削圆上，砂轮绕砂轮架回转中心O'2转动角度 θ2，到达位置 ΔO'2A1B1。经研究发现［2－3］，砂轮回转台绕自身的回转中心O2回转的角度与圆插补轨迹的回转角度有一定的几何关系，即θ2=θ3。

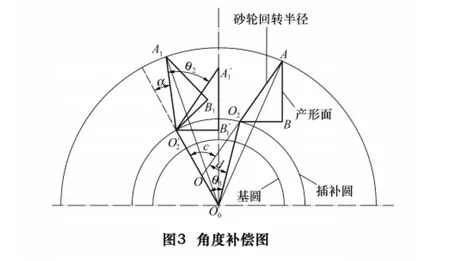
ΔO2AB随插补运动平移至ΔO'2A1'B'1位置时，绕过O'2的B轴转动的角度θ2与回转工作台随插补运动转过的角度θ3相等时，砂轮磨削边缘点的位置正好在磨削圆上，满足加工要求。

3 数学建模

3.1 坐标架设定

X向、Z向导轨、砂轮回转台、主轴等部件可视为刚体，可以用齐次坐标变换矩阵来描述机床的运动。根据图1所示的加工原理和包络环面成形原理，设置坐标架如图 4，其中 σ（O0;x0，y0，z0）为定标架，O0为虚拟插补圆圆心，过O0点作经蜗杆轴心线的平面W。σ1（O1;x1，y1，z1）为设置在蜗杆上的的定标架，O1为喉颈中心线与蜗杆轴心线的交点，在平面W内O1O0为啮合中心距a，X方向由O1指向O0，Z沿蜗杆轴心线方向，Y与X、Z符合右手笛卡尔坐标系。为了简化计算，在砂轮回转台上设置定标架 σ2（O2;x2，y2，z2），在X向工作台上设置 σ3（O3;x3，y3，z3），在Z向工作台上设置 σ4（O4;x4，y4，z4），在主轴上设置 σ5（O5;x5，y5，z5）。各定标架的X、Y、Z方向相同。

假设在初始位置时，坐标系 σ2、σ3、σ4重合，原点O2、O3、O4重合且为砂轮回转工作台回转轴在平面W上的垂足，设其在定标架σ0中的坐标为（x0，0，z0）。同时假设坐标系σ1与σ5重合，原点O1与O5重合且在σ0中的坐标为（－a，0，0）。在砂轮产形面与蜗杆相截平面的瞬时接触线上任取一点P，设O0P为r，O1P为r1，O2P 为 r2。

3.2 坐标变换矩阵

（1）根据齐次坐标变换理论［4］，当砂轮回转台作B轴逆时针转动φ2时，定标架σ2相对于σ3的齐次坐标变换矩阵为

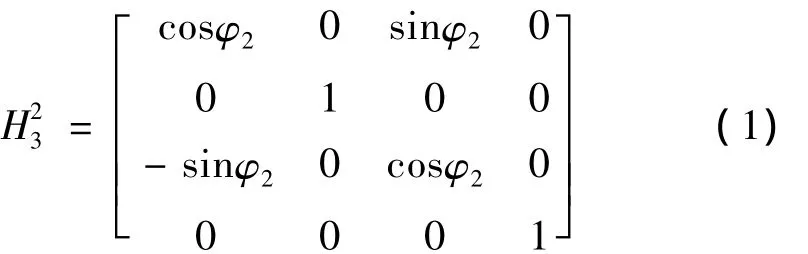
（2）当工作台沿着X方向运动x时，定标架σ3相对σ4的齐次坐标变换矩阵为

（3）当工作台沿着Z向运动z时，由于定标架σ4的原点在 σ0中的坐标为（x0，0，z0），因此定标架 σ4相对于σ0的齐次坐标变换矩阵为

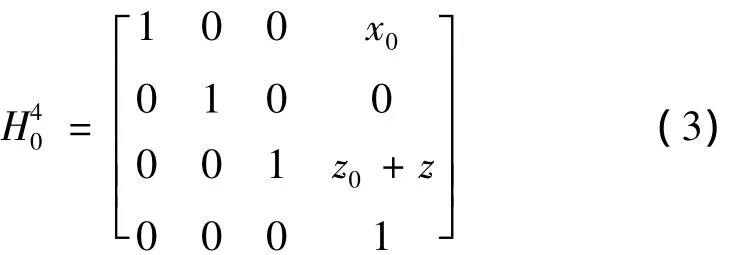
（4）当主轴绕着C轴顺时针转动φ1时，定标架σ1相对σ5的齐次坐标变换矩阵为

（5）由于 σ5的原点在 σ0中的坐标为（－a，0，0），因此定标架标系σ5相对于σ0的齐次坐标变换矩阵为

P点在砂轮产形面与蜗杆相截平面的瞬时接触线上，因此在理想状态下砂轮产形面上的点P（x2，y2，z2）应与蜗杆上的点D（x1，y1，z1），在定标架 σ0中重合。

设置在砂轮回转台上的定标架σ2相对σ0的齐次坐标变换矩阵传递链为:砂轮回转工作台→X向工作台→Z向工作台→定标架σ0。

设置在蜗杆上的定标架σ1相对定标架σ0的齐次坐标变换矩阵传递链为:蜗杆→主轴→定标架σ0。

由上面的推导可得到为

代入后计算得到为

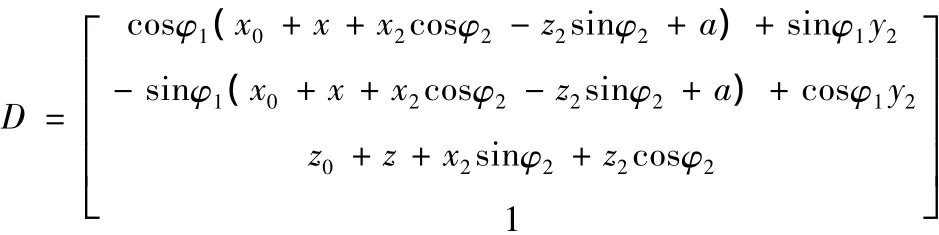
4 加工模型

4.1 啮合方程和啮合函数

在数控加工过程中砂轮回转台、Z向导轨和X向导轨的合成运动为在σ0（O0;x，y，z）中以r为半径，以ω2为角速度绕B轴的转动。

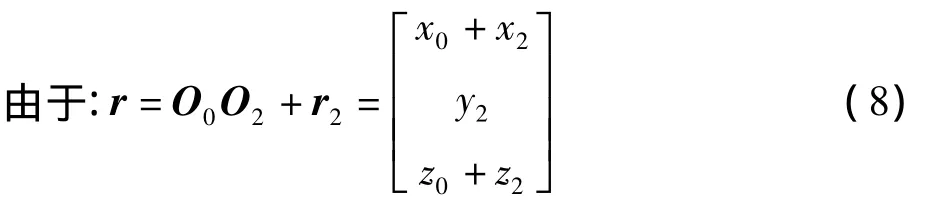
则:P（x2，y2，z2）点在 σ0（O0;x，y，z）的坐标为（x0+x2，y2，z0+z2）。

取动标架 σ'0（O'0;x'，y'，z'），在初始位置时与 σ0（O0;x，y，z）重合。当砂轮回转工作台绕B轴转动时，动标架σ'0也绕B轴转动相同的角度。

下面在动标架 σ'0（O'0;x'，y'，z'）中进行分析:

啮合函数和啮合方程依次为

其中:n为啮合点P处的单位法向量;v21为啮合点P处的相对速度向量。

相对速度的表达式为

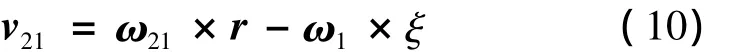
由图4可得到为

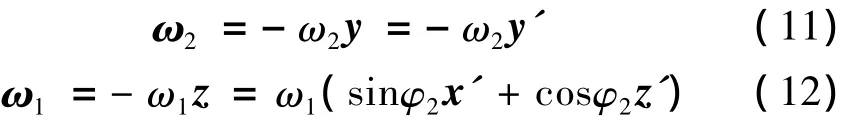
为了简化运算，令 ω1=1，则 ω2=i21，因此 ω2= －i21y'，ω1=sinφ2x'+cosφ2z'

则

则

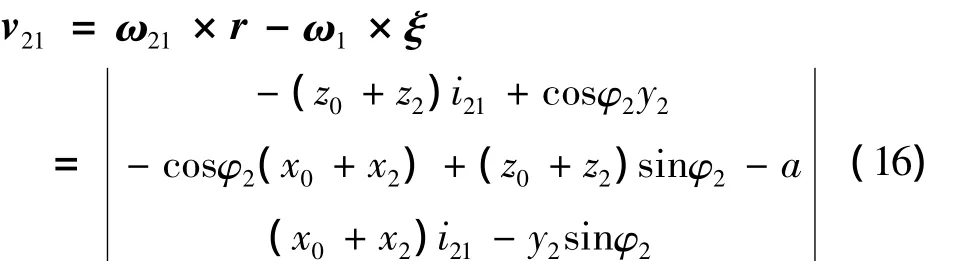
如图5所示，在砂轮产形面上设置定标架σ6（O6;x6，y6，z6），其原点在 σ2（O2;x2，y2，z2）中的坐标为（0，0，b），与B点重合。X方向与σ2（O2;x2，y2，z2）的X方向相反，Y方向与σ2（O2;x2，y2，z2）中的Y方向夹角为β。σ6（O6;x6，y6，z6）与 σ2（O2;x2，y2，z2）是固联在一起的。

设P在 σ6（O6;x6，y6，z6）中的坐标为（u，v，0），在产形面内过P作垂线，与产形面和底面W的交线垂直，垂足为P0，PP0长度为v，P0到定标架 σ2（O2;x2，y2，z2）的Z轴的距离为u。则P在σ2中的坐标为（x2，y2，z2）=（－u，－vcosβ，b－vsinβ），在动标架 σ'2中，产形面方程为

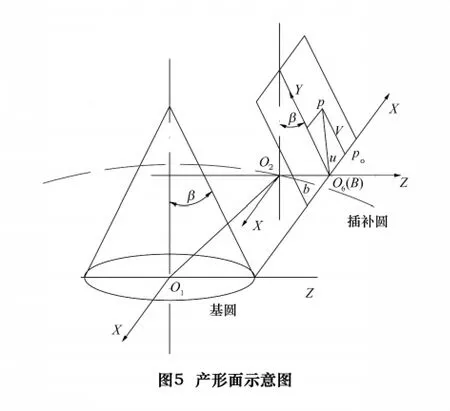
于是:ru=（－1，0，0），rv=（0，－cosβ，－sinβ）

单位法向量为

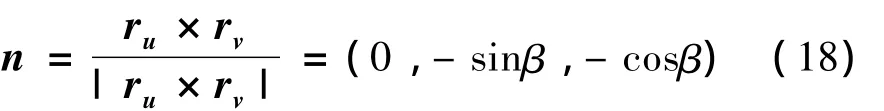
把n、v21代入得啮合方程为

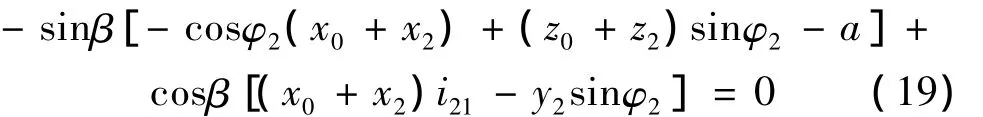
当 sinφ2≠0 时，把（x2，y2，z2）=（－u，－vcosβ，b－vsinβ）代入，整理得到为

4.2 砂轮上的瞬时接触线方程

根据啮合理论知识，砂轮产形面上的瞬时接触线方程为

将（x2，y2，z2）=（－u，－vcosβ，b－vsinβ）与上式联立，即可求出在定标架σ2中的瞬时接触线的方程为

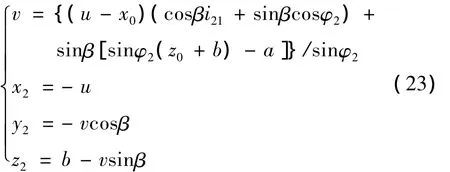
按上式确定瞬时接触线的步骤为:

（1）根据设计要求和机床的参数，确定a、i、β、b;

（2）确定初始位置（x0，0，z0）;

（3）确定u的取值范围;

（4）给定φ2一个值（在规定的取值范围内），取一系列的u值，则由式（23）中的第一式求出与之对应的一系列的v值;

（5）将求出的一系列v值依次代入式（23）中后面3个式子中，就求出一组相接触点的坐标;

（6）利用平滑曲线连接这些坐标点，即可确定一条瞬时接触线;

（7）再给出一个φ2值，重复上述步骤，求出另一条瞬时接触线。依此类推，即可求出在选定的β值下的一系列瞬时接触线。

4.3 蜗杆齿面方程

把接触线方程由定标架σ2转到σ1，则与之共轭的就是蜗杆齿面的接触线，可求得蜗杆齿面方程［5－6］。蜗杆齿面的坐标方程式为

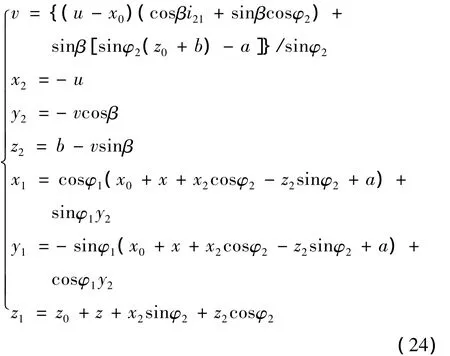
上式中 φ1、u是蜗杆的独立参数，确定（x0，y0，z0）后当给定一个φ2值，取不同的u值就可以得到一系列的点（x1，y1，z1），把这些点用平滑的曲线连起来，就得到坐标系σ1上的一条接触线。每给出一个φ1，就可以得到一条接触线，依此类推，可以求出多条接触线，这些接触线的集合就是蜗杆齿面。

5 磨削实验

采用基于CDK6150数控车床改造的平面二次包络四轴四联动数控磨床（如图6）进行磨削实验。实验加工的蜗杆的主要参数见表1。加工蜗杆的程序如下:

主程序:

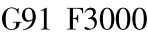
子程序P12:

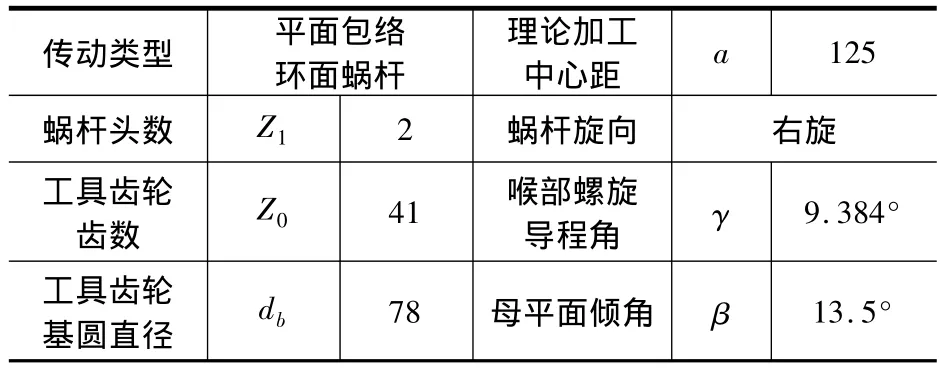
表1 平面二次包络蜗杆主要参数

根据磨削原理，利用平面二次包络四轴四联动数控磨床加工出的平面二次包络蜗杆如图7所示，该数控磨床加工调整及操作方便，效率较高。通过对比，磨削加工的蜗杆质量及表面粗糙度与加工二次包络蜗杆普通磨床相比有较大改善，蜗杆的表面粗糙度和精度均能够达到要求，效果很好。

6 结语

通过大量的切削实验证明，自主研发的平面二次包络四轴四联动数控磨床能达到加工生产要求，它可以加工中心距80～500 mm，蜗杆头数l～8头的相应模数的蜗杆;既能加工环面包络蜗杆，也能加工圆柱、螺纹蜗杆。这也充分说明平面二次包络四轴四联动数控磨床的加工工艺原理正确、可行，该磨床具有一定的推广价值。但是在实践中一些问题仍有待解决，如:当加工不同工件时砂轮头的位置需要调整，使砂轮头的回转力臂发生变化，从而使精度的稳定性受到影响，还有如何提高数控插补精度等深层次问题。相信经过研究和改进，机床的质量会有进一步提高。

［1］和法洋，黎帆，张珂，等.平面二次包络四轴四联动数控磨床数学建模及精度分析［J］.机床与液压，2009，37（11）:11 －13.

［2］龙宇，黎亚元，刘洁.平面二次包络环面蜗杆的一种新加工工艺及加工精度分析［J］.制造技术与机床，2007（5）:80－83.

［3］陈金成，徐志明，钟进修，等.机床沿曲线高速加工时的运动学与动力学特性分析［J］.机械工程学报，2002，38（1）:31 －34.

［4］赵宁，刘常青.关于面齿轮磨削加工机床的研究［J］.机械设计与制造，2007（10）:151－152.

［5］韩兴国，崔立秀，王斌武，等.基于动力学和运动学的开放式数控系统圆弧插补轨迹研究［J］.组合机床与自动化加工技术，2009（5）:75－77.

［6］廖效果，朱启逑.数字控制机床［M］.武汉:华中科技大学出版社，2003.