基于运动微分方程特征值的转子-轴承系统失稳可靠性分析*
赵群超 张义民
(东北大学机械工程与自动化学院,辽宁沈阳 110819)
近些年,国内和国际上,许多大型、高速的旋转机组都发生了或大或小的油膜失稳事故,并造成了重大的经济损失。转子-轴承系统的失稳问题关系到企业生产的安全、规模、能力,以及对应的效益。对于一个企业而言,生产中的稳定性是实现高效生产的重中之重。多年来,许多学者和研究机构对转子-轴承系统的稳定性进行了一系列的研究和探索[1-4]。文献[1]对线性系统的稳定性定义为:如果一个系统受到扰动后,系统最终可以返回原先的平衡状态,则这一系统的平衡状态是稳定的;如果受扰后,系统无限偏离原先的平衡状态,则这一平衡状态时不稳定的。对于转子-轴承系统,其在运转过程当中会发生动力失稳,这一不稳定性问题的原因主要是因为整个系统本身存在着负阻尼和交叉刚度。基于这个最基本的原因,本文从转子-轴承系统的运动方程入手,以单圆盘对称支撑的转子-轴承系统为例,来分析系统失稳的一系列可靠性问题。
1 运动方程及其特征值与系统失稳的关系
具有n个自由度的转子-轴承系统(线性系统)的运动方程可用式(1)所示的二阶矩阵微分方程表示
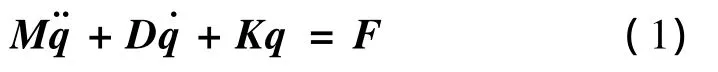
式中:M、D、K分别是系统的质量、阻尼和刚度矩阵(维数为n);q、F为位移矢量和激振力矢量。
研究稳定性主要是针对系统的自由振动方程,它是式(1)的齐次方程,即
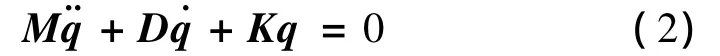
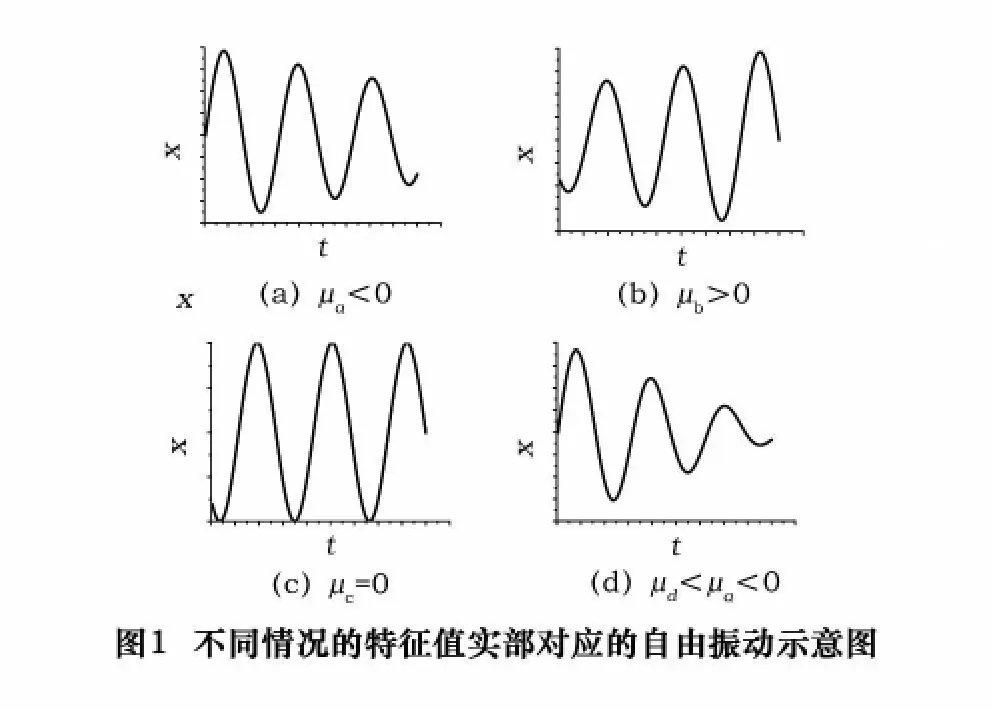
对于式(2),经过计算可得到其特征值ν,ν的形式为μ±jω。当μ<0,即所有特征值都具有负实部,此时,式(2)描述的自由振动随着时间的增加振幅不断衰减并最终衰减至零,此时的振动是稳定的衰减振动,如图1a所示。当μ>0,即特征值(至少有一个)的实部大于零,此时,式(2)描述的自由振动随着时间的增加振幅不断增大并最终为无穷大,此时的振动称为不稳定振动,如图1b所示。当μ=0,即特征值的实部等于零(不为零的实部要小于零),此时,式(2)描述的自由振动处于一种平衡状态,称为稳定性界限状态,如图1c所示。
2 稳定性裕度评估
设计一台旋转机械的时候,为了使得其具有良好的稳定性能,仅仅保证其工作在稳定的区域是不够的。在此基础之上还要保证它具有足够的稳定性裕度,用来抵抗外界的各种干扰。图1d所示的自由振动与图1a相似,都具有负的特征值实部,但是情况d的实部比情况a的实部要小,所以情况d的自由振动衰减得更快,有更强的能力来抵抗外界的干扰。对于这两种情况,需要寻找一个客观的判据来评定它们的优劣性。一般的,设计人员采用以下3个判据来评估系统的稳定性裕度:(1)对数衰减率判据;(2)失稳转速判据;(3)减稳因素界限值判据[1,3]。虽然应用以上的这些判据,可以判定出哪一组设计参数更为合理,但是这种判定只能粗略地对系统的稳定性裕度进行评估。为了更精确地、定量地、明了地做出稳定性裕度评估,以下我们根据可靠性分析的方法,合理地给出了解决办法。
2.1 系统状态函数的选择
因为系统稳定需要所有特征值的实部都为负值,所以也可以将整个系统的稳定问题看成是多个子系统串联形式的可靠性问题,每一个特征值都为负值时,系统才能稳定运行。从可靠概率的意义可知,系统的可靠度计算式为:
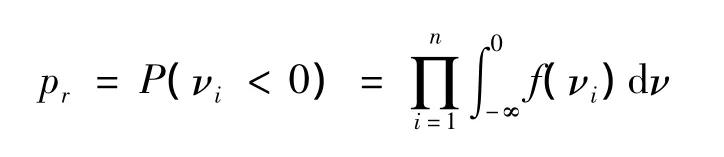
式中:pr为可靠度计算符号;P()为求概率函数;f(νi)为νi的分布密度函数;n为特征值个数。
但是,对于以特征值来度量系统稳定性的问题,按照串联形式计算的结果趋于保守。对于单圆盘对称转子来说,特征值ν跟通常是两对共轭复根[6],而且一般情况下,在整个工作频率范围之内,2个特征值实部不发生交叉,也就是说2个特征值实部有恒定的大小关系。所以,在不失反应度量准确性的情况下,将系统状态函数g(X)定义为:
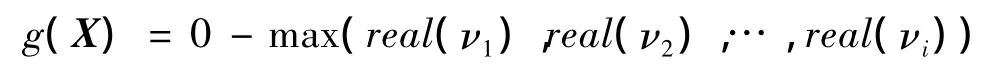
式中:real()为对实数取实部函数;g(X)<0为失稳状态;g(X)=0为临界状态;g(X)>0为稳定状态。
此时:pr=P(g(X)>0)
2.2 稳定性裕度的可靠性分析
根据二阶矩阵微分方程的求解方法,求解方程(1)的特征值的问题可归结为求下式特征值问题,

式中:ν为特征值;{ψ}为对应的特征向量。
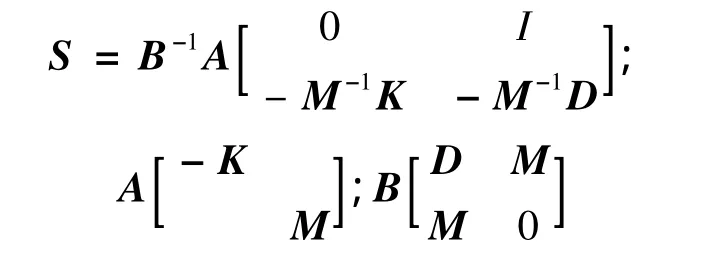
在工程生产中,加工的误差,安装的误差,以及工况的改变等等这些不可避免的实际情形使得决定系统稳定的各个参数会发生或大或小的变化。实践证明,这些变化一般不会远离额定参数数值。所以,可将这些变化看成是关于额定参数的一种摄动行为。
根据可靠性分析的随机摄动理论[5],g(X)为系统随机参数向量X的函数。X和g(X)可表示为
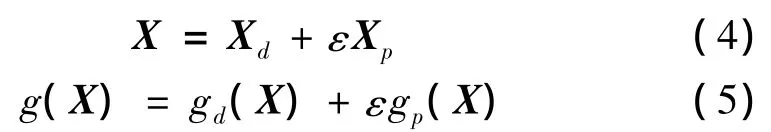
式中,ε为一小参数,下标为d的部分表示随机参数中的确定部分,下标为p的部分表示随机参数中的随机部分,且具有零均值。显然要求随机部分要比确定部分小得多。
对式(4)、(5)取数学期望,有
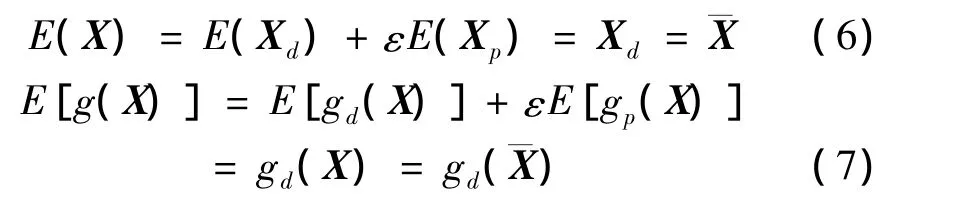
同理,根据Kronecker代数理论,随机参数X和状态函数g(X)的方差可分别表示为
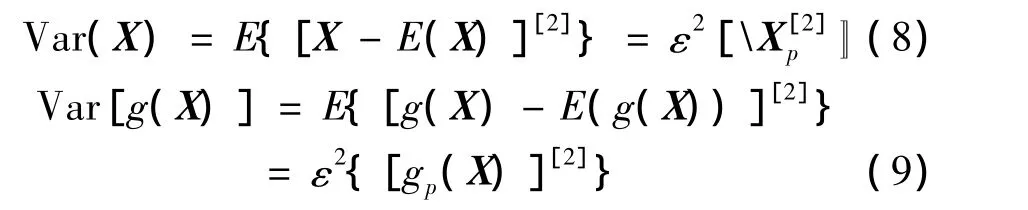
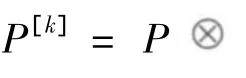
根据向量值和矩阵值函数的Taylor展开式,当随机参数的随机部分比其确定部分小得多时,可以把gp(X)在E(X)=附近展开到一阶为止,有
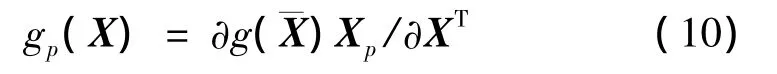
把式(10)代入式(9),有
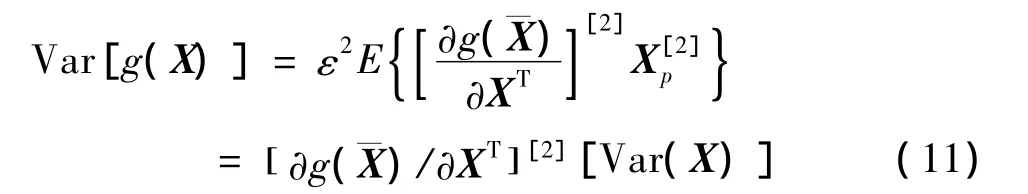
其中,g(X)为系统状态函数,X为系统随机参数向量,为随机参数向量X的均值。
可靠性指标定义为
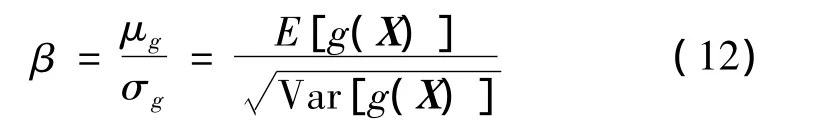
设基本随机变量向量X中的所有元素服从正态分布,用失稳点处状态表面的切平面近似地模拟极限状态表面,可以获得可靠度的一阶估计量

3 数值算例
某由动压向心滑动轴承对称支撑的单圆盘转子-轴承系统,其部分参数的期望值已知(如表1),其中各变量及动特性指标的变异系数统一按0.05进行计算。试进行转子-轴承系统失稳的可靠性分析。

表1 各变量期望值
根据给出的已知参数估算出系统的失稳转速在3 000~4 000 r/min之间,估算方法见参考文献[6]。之后在文献[7]上查得在如上条件下,转速在2 781 r/min与4 218 r/min时滑动轴承动特性系数值,如表2所示。在编程时以插值的方法计算出每个计算点的动特性系数值,从而计算出相对准确的fi(X)。
经过编程运算,得到系统的特征值ν具有两对共轭复根,形式为a1,2±b1,2j;a3,4±b3,4j。将实部a提取出来列成图2a所示。在2 718~4 218 r/min转速之间,a1,2的绝对值相对于a3,4大很多,图 2a 显示的实部随转速的走向对比不明显,所以将高转速下过大的实部省去,将2 718~3 548 r/min转速之间实部值绘制的出来,如图 2b 所示。实部a1,2,a3,4起始随转速的增加都是在减小,在3 300 r/min左右,a1,2达到最小,然后增大,突破零线后迅速增大。
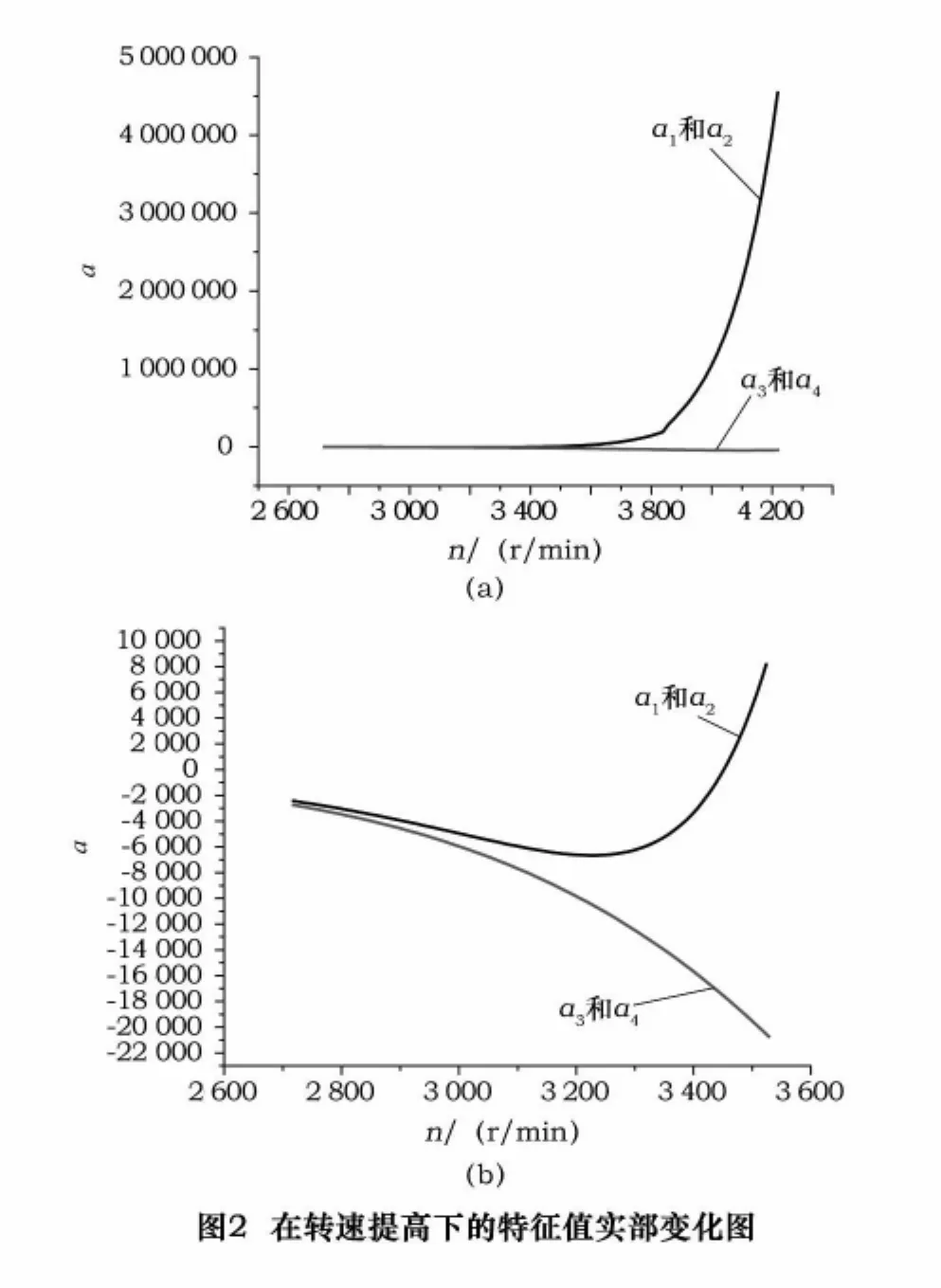
根据之前设定的系统状态函数,这里把a1,2作为主要研究对象,绘制其随转速增大的曲线如图3所示。特征值实部a1,2在工作转速达到3 470 r/min左右达到零值,此时,系统处于临界状态。
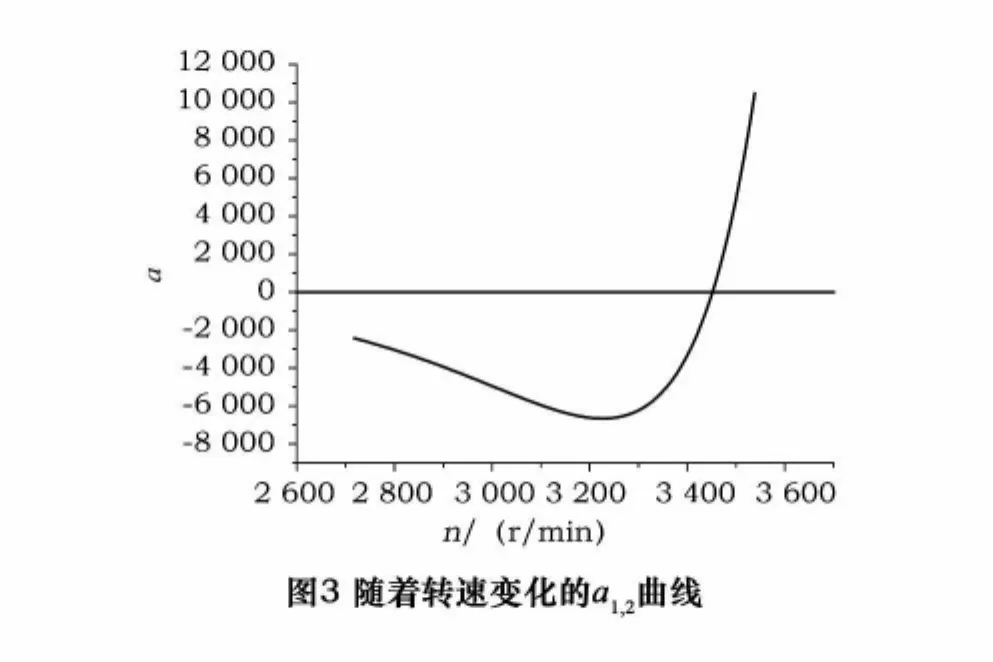
图4列出了系统在4 218 r/min转速以下关于失稳的可靠度曲线。系统在3 420~3 480 r/min转速附近可靠度迅速下降,直至完全失稳状态。这与图3所示在零点附近特征值实部相对于转速增加急速增大非常吻合。说明了所得到的可靠度曲线,真实地反应了系统实际的工作状态。综上分析,在工程上,设定工作转速的时候,对于上述的转子系统要将工作转速设定在3 420 r/min以下,最佳工作转速应在3 300 r/min附近。这样设计的工作转速会在很大程度上提高系统在抵抗失稳上的裕度,增强系统的可靠性。

表2 滑动轴承的动特性系数值
4 结语
经上分析,以转子-轴承系统运动微分方程的特征值来度量系统的稳定性是可行的。这种方法可以准确地指出系统失稳的临界状态的位置,指导工程中设定的工作参数可以避开系统失稳区域。这种方法还可以明确地给出系统失稳裕度的最大点,给工程人员在设计时提供合理的参考数据。
[1]徐龙祥.高速旋转机械轴系动力学设计[M].北京:国防工业出版社,1994.
[2]Lund JW.Stability and damped critical speeds of a flexible rotor in fluid- film bearing[J].Journal of Engineering for Industry,Trans.of ASME,1974,96(2):509 -517.
[3]张直明,虞烈.滑动轴承-转子系统阻尼值与稳定裕度的相互关系[J].上海工业大学学报,1985(4):11 -20.
[4]徐祥龙,朱均.大型发电机组稳定性研究[J].机械工程学报,1992,28(3):6-11.
[5]张义民.汽车零部件可靠性设计[M].北京:北京理工大学出版社,2000.
[6]张直明,张言羊,谢友柏,等.滑动轴承的流体润滑理论[M].北京:高等教育出版社,1986.
[7]机械设计手册编委会.机械设计手册单行本(滑动轴承)[M].北京:机械工业出版社,2007.

