商贸流通业与天津经济增长的实证分析
吴爱东,褚俊玲
(天津商业大学经济学院,天津300134)
天津经济在快速发展的同时面临产业结构发展的不平衡。2009年全国三次产业结构为10.3%、46.3%、43.4%;上海为 1%、47.4%、51.6%;北京为 1%、23.5%、75.5%;同期天津为1.7%、53.0%、45.3%。如果第二产业和第三产业不能协调发展,势必会影响天津经济快速、持续增长。商贸流通业①是第三产业的主体,本身高速发展将直接提高第三产业比重;商贸流通业的产业融合,正在进一步向第三产业等其他领域渗透,大型零售商业集团把经营触角伸向房地产业、饭店业、租赁业、旅游业、娱乐业等多种产业领域,形成一种复合型的新兴产业,从更大程度上影响着资源配置和产业结构的优化;商贸流通业通过集中采购在区域和全球范围内构建整个市场流通体系,通过控制流通渠道决定着制造业,主导着消费市场,影响着金融市场的稳定和商业环境的优化。以商贸流通业为核心的现代服务业的发展,将成为天津经济转变经济发展方式的重要通道,成为天津产业结构升级的重要支撑。
商贸流通业在改革开放前后到底发生了怎样变化以及流通业发展对天津经济的促进作用到底有多大,这些问题目前并没有准确的答案。本文将在已有研究成果的基础上,对1949—2009年天津GDP和商贸流通业增加值数据以1978年为界分为改革前(1949—1978年)和改革后(1979—2009年)两个阶段,用回归分析和误差修正模型两种方法定量分析商贸流通业在改革前后发生的变化及其与经济增长之间的关系。
1 文献综述
目前,国内对于商贸流通业与经济增长的关系的研究并不少见。晏维龙等从理论上分析了城市与流通业发展的关系,构建了1960—2001年我国城市化率与商品流通的分阶段回归模型,提出“流通先导”的发展战略。[1]冉净斐运用菲德模型对1980—2001年中国流通业推动经济增长的全部作用和外溢效应贡献进行经济计量测算,结果证实了流通与经济增长具有正的相关关系。[2]宋则在研究流通现代化及流通业竞争力时,提出了用流通业贡献率指标衡量流通业对经济发展的影响。[3]王德章、宋德军利用1990—2005年全国及北京、哈尔滨、贵阳的流通业发展水平和代表城市经济发展指标的年度数据,用自回归分布滞后模型建立对应的误差修正模型,定量分析流通业对城市经济发展的影响因素,提出以流通业为先导,促进流通业与城市经济发展的建议。[4]唐红涛采用1995—2007年的面板数据,运用聚类分析方法就我国各省区流通业对区域经济的影响进行计量分析,结论是:流通业是区域经济增长的重要动力,但是流通业对区域经济增长的弹性与当地区域经济总量有着密不可分的关系,中国发展流通业应该因地而异。[5]
上述研究从不同的角度,分析了商贸流通业对城市经济发展的影响,并运用实证分析从不同角度加以证明,同时提出了以流通业为先导,以流通业促进城市经济发展的政策建议。以上研究大部分选取社会消费品零售总额作为商贸流通业发展的指标,社会消费品零售总额中不仅有流通业的销售额,还有制造业、农业等产业的销售额,而且,流通业不仅从事着消费品的销售,还有生产资料的销售。所以采用商贸流通业增加值的指标更为科学。此外,1978年改革开放以来,商贸流通服务业本身的管理体制、经营机制发展经历了巨大变革,国民经济发展的影响也表现出明显的阶段性,这一点在上述文献中大多没有给予足够的注意。
因此,本文以1978年为界,用定量方法分阶段研究商贸流通业对天津经济发展的影响力。
2 天津商贸流通业发展及其对国民经济的贡献分析
天津作为中国北方最大的经济中心和港口城市,伴随着天津发展模式的全面转型、产业结构调整及居民消费升级步伐的加快,天津商贸流通业的发展将打通天津经济快速发展的高效路径。为了更加准确清晰地描述天津商贸流通业对国民经济的影响,现通过商贸流通业对GDP的贡献率和商贸流通业拉动经济增长的百分点这两项指标来分析天津商贸流通业对国民经济发展的作用,从整个发展历程来分析天津商贸流通业对国民经济发展的贡献。
从1949—2009年发展历程看,在1949—1977年整个计划经济阶段,天津商贸流通业对GDP的贡献率尽管起伏较大,从总的趋势看是逐年下降的。从1950年的85.50%下降到1977年的3.80%。1950年,商贸流通业对GDP的贡献率高达85.50%,这一时期天津作为中国北方经济中心,在中国经济中发挥重要作用,也是天津经济发展最快时期;与改革开放前相比较,改革开放后商贸流通业对经济发展的贡献是相对稳定的。其中1993年为31.12%,以后两年贡献率呈下降趋势,1995年下降到16.3%,其后贡献率指标有所上升,1998年达到最大贡献率38.99%。至此以后,贡献率降多升少。

图1 天津市1949—2009相关经济指标变化趋势
从拉动经济增长百分点指标的走势看,改革开放前的指标波动幅度较大,期间出现了一个明显的波峰和一个明显的波谷,波峰出现在1950年,达到这个指标的最大值21.13%,波谷出现在1954年,仅为-7.79%。1961年的三年困难时期,商贸流通业,拉动经济增长百分点是-1.80%,形成历史的最低点。改革开放以后,随着天津市场经济的发展和新的流通体制的建立,这个指标总的趋势是逐年上升的,从1979年的1.43%增加到2009年的4.35%。但这个指标的数值没有太大的波动,基本保持在2% ~5%,仅在1984年和2004年产生小幅上升。
从以上分析可以看出,商贸流通业对于促进天津经济发展具有不可替代的作用。为了更加直观地描述两者的长期均衡关系,本文采用协整分析和误差修正模型对其进行进一步研究。
3 天津商贸流通业与GDP协整性实证分析
3.1 协整检验与误差修正模型
3.1.1 协整检验
协整是对非平稳经济变量间存在的长期稳定的均衡关系的统计描述。协整检验有两种方法:一是Engle-Granger两步法;二是 Johansen检验法。前一种方法适合于检验两个变量之间的协整关系,后一种方法用于检验多个变量之间的协整关系。由于本文研究的是商贸流通业增加值与GDP这两个变量之间的关系,因此,采用第一种方法来检验变量之间的协整关系。
Engle-Granger两步法的基本原理是:若变量xt和Yt都是d阶单整的,用一个变量对另一个变量回归,即有:


第一步:在假设协整成立时,对(1)进行最小二乘估计,得到协整向量的估计值;第二步:将第一步的结果用于估计ECM。因此,协整检验就转化为对(2)式得到的残差估计值进行单位根检验,如果是d阶平稳的,则变量Xt和Yt具有协整关系,且(1,-)为协整向量,方程(1)为协整回归方程。
3.1.2 误差修正模型
按照Granger定理,如果两变量Xt和Yt是协整的,则它们之间的短期非均衡关系总能有一个误差修正模型表述。误差修正模型的表达式是:

其中 ECMt=Yt-k0-k1Xt,是非均衡误差。
Yt=k0+k1Xt表示 Yt和 Xt的长期关系;β1ECMt-1为误差修正项;β1是修正系数,表示误差修正项对DYt的修正速度。根据误差修正模型的推导原理,因β1的值为负,误差修正机制应该是一个负反馈过程。k0和k1是长期参数,β0和β1是短期参数。
3.2 实证研究
3.2.1 改革开放前1949—1978年天津商贸流通业与GDP协整分析
(1)时序图。为了降低数据的波动性,对表中的商贸流通业增加值和国内生产总值取对数,其中lnSMZ和lnGDP代表商贸流通业增加值和国内生产总值的对数值。对数图见图2,可见商贸流通业增加值和国内生产总值存在较强的相关关系。
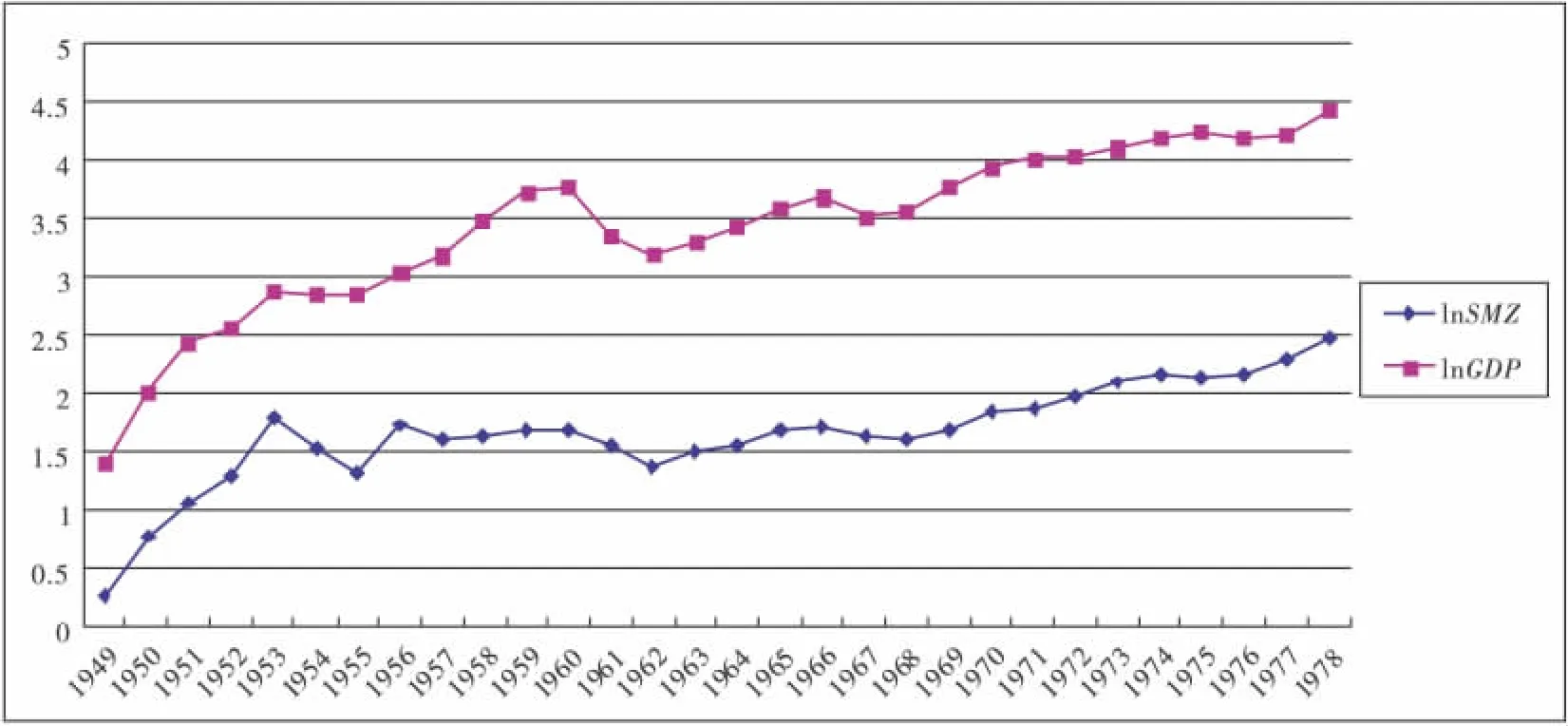
图2 商贸流通业增加值和GDP的对数数据图
(2)平稳性检验。分别对lnGDP和lnSMZ数据进行单位根检验,利用Eviews 5.0,分析结果见表1。
由表1可知,取对数后的GDP和商贸流通业增加值在5%显著水平下均为一阶平稳,二者是一阶单整的。所以可以用EG两步法做协整回归并检验对数之后天津GDP和商贸流通业增加值是否存在协整关系。
(3)协整检验与误差修正模型。运用最小二乘法对商贸流通业和GDP的关系进行回归分析。运用Eviews 5.0统计分析软件,得出回归方程如下:

检验(4)式残差e1,平稳性检验如上表最后一行所示,残差在5%显著水平下为平稳序列,表明序列lnGDP和lnSMZ具有协整关系。同时,本文也对lnSMZ关于lnGDP做出协整检验,结果显示,lnSMZ关于lnGDP协整方程的残差不具有稳定性,表明lnSMZ关于lnGDP不存在长期均衡关系。主要原因是,改革开放前,生产决定流通,商贸流通业基本上是一个计划经济体制下的特定部门。
按照Granger定理,具有协整关系的变量一定具有误差修正模型的表达形式存在。用(4)式中求得的残差e1作为非均衡误差,按照由一般到特殊的方法剔除不显著的变量,逐步回归,得到GDP和商贸流通业增加值的误差修正模型:
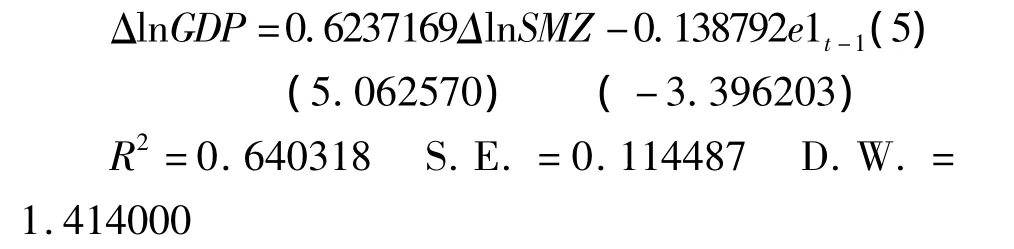
其中,e1t=lnGDPt-2.752903 -0.640659 lnSMZt
误差修正系数为-0.138 792,小于零,符合反响修正机制。由(4)式中的协整回归式可得lnGDP关于lnSMZ的长期弹性为0.640 659,由(5)式可得lnGDP关于lnSMZ的短期弹性为0.627 169,改革前的1949—1978年,流通业对天津GDP的增长具有重要作用。
3.2.2 改革开放后1979—2009年天津商贸流通业增加值与GDP协整分析
(1)时序图。对商贸流通业增加值与GDP取对数,对数图如图3所示。
图3表明lnGDP和lnSMZ具有大致相同的增长和变化趋势,说明二者可能存在协整关系。

图3 1979—2009年商贸流通业增加值和GDP的对数数据图
(2)平稳性检验
分别对lnGDP和lnSMZ数据进行单位根检验,Eviews分析结果见表2。
由表2可知,取对数后的GDP和商贸流通业增加值在5%显著水平下均为一阶平稳,即两者是一阶单整的。
(3)协整检验。下面就采用 EG两步法对lnGDP和lnSMZ进行协整检验。用传统的OLS方法进行回归,得到以下的回归方程:
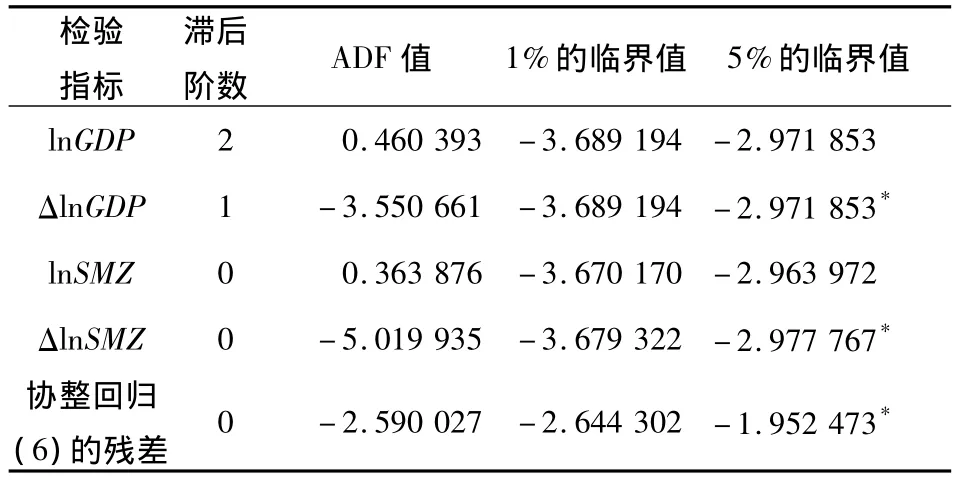
表2 lnGDP和lnSMZ的平稳性检验结果

(6)和(7)两个回归方程的残差记为e2和e3,二者的ADF检验结果见表3。
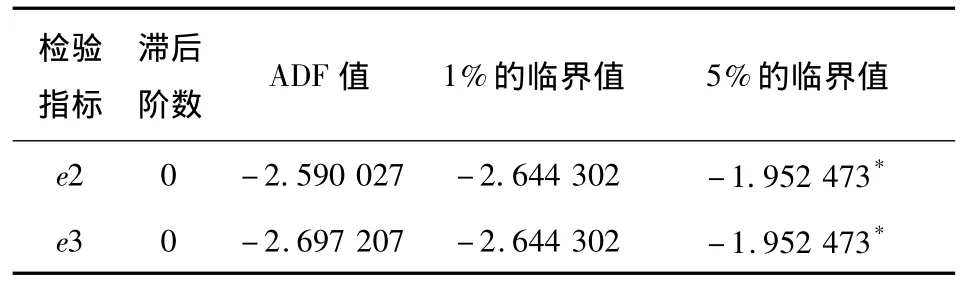
表3 e2和e3的ADF检验结果
由表2可以看出回归模型所反映的lnGDP和lnSMZ的协整关系成立,说明天津商贸流通业和GDP之间存在长期稳定的关系,二者可以互相解释。
(4)误差修正模型
按同上方法,用(6)式中求得的残差e3作为非均衡误差,得到改革后天津GDP和商贸流通业增加值的误差修正模型:

其中,e2t=lnGDPt- 2.180692 -0.917561 lnSMZt(ar(1)=0.583692)
误差修正系数为-0.187 989,小于零,符合反响修正机制。由(6)式中的协整回归式可得lnGDP关于lnSMZ的长期弹性为0.917 561,由(8)式可得lnGDP关于lnSMZ的短期弹性为0.279 919,改革开放后商贸流通业拉动经济增长的作用进一步增强。
4 结论及建议
4.1 结 论
(1)根据得到的误差修正模型:从长期看,天津商贸流通业与经济增长之间有均衡的动态关系。由模型方程(4)和(6)可知改革开放后的天津商贸流通服务业对经济增长的影响力更大。1949—1978和1979—2009年商贸流通业的弹性系数分别为0.640 659和0.917 561,表明商贸流通业增加值每增加1个单位,可拉动的经济增长分别为0.641 659和 0.917 561 个单位。
(2)从模型方程(7)也可以看出,改革开放后,由于流通业在国民经济中的作用进一步增强,GDP的增长同样对商贸流通业的发展产生巨大的推动作用,GDP的弹性系数为1.065 767,说明GDP每增长1个单位,商贸流通业增加值将提高1.065 767个单位。
(3)根据模型方程(5)和(8),从增长率角度看,天津商贸流通业增加值每增加1个单位,1949—1978年和1979—2009年两个阶段 GDP的增长分别为0.627 169和0.279 919个单位。
(4)从短期来看,商贸流通业的发展和GDP的变动会出现不一致的时候,这种情况可以用误差修正模型来解释。从模型方程(5)和(8)可以看出,1949—1978年和1979—2009年的修正比率分别为0.138 792 和0.187 989,即如果 Et-1 等于1%,由天津经济系统本身的修正作用会使下期的ΔlnGDP分别减少0.138 792 和0.187 989。
4.2 建 议
(1)充分认识商贸流通业发展在天津经济发展中的重要作用,要从战略高度统筹流通产业的发展规划。整合天津商贸流通资源,建立商品畅销体系,大幅降低流通成本。构建城乡一体化、内外贸一体化、批发零售物流配送一体化的商贸物流渠道网点,构建现代化、竞争性、高效能、低成本的流通体系。
(2)创造有利于天津商贸流通业发展的市场环境,构建强大的商贸流通主体。加快培育和发展一批大企业、大集团,针对天津商贸流通企业规模较小,集中度低,按照建立现代企业制度的要求,加大银行信贷、税收、工商管理进出口渠道等方面的政策扶持力度,以业态融合和价值链整合为方向,通过兼并、联合、重组等方式,尽快培育和发展一批实力强、管理规范的跨地区跨所有制的大型企业集团,做大做强天津商贸流通的主体,为商贸流通业快速、持续发展提供有利条件。
(3)推进天津商贸流通业现代化。在制度与技术方面,以提高流通效率为基准,做好企业制度、市场制度以及政府宏观调控的创新,运用现代信息技术改造传统落后的流通结构,发展现代化的流通方式,提高商贸流通业竞争力。
(4)加强教育,引进人才,构建可持续的人才保障体系。商贸流通业人才是推动天津商贸流通业发展的重要力量,坚持培养与引进相结合,制定商贸流通产业人才培养规划,优化人才培养环境,加强企业家、职业经理人、专业技术人员和高技能人才培养,注重商贸流通业人才的引进,形成天津商贸流通业的快速、持续发展推动力。
注 释:
① 商贸流通业范畴主要是指批发业、零售业及专门为商业服务的仓储、交通运输及邮政业行业。商贸流业对GDP的贡献率=(当年商贸流通业增加值—上一年商贸流通业增加值)/(当年的GDP值—上一年的GDP值);商贸流通业拉动经济增长百分点=商贸流通业对GDP的贡献率×GDP增长速度;GDP增长速度=(当年的GDP值—上一年的GDP值)/上一年的GDP值。
[1]晏维龙.城市化与商品流通的关系研究:理论与实证[J].经济研究,2004(10):40 -42.
[2]冉净斐.流通发展与经济增长的关系:理论与实证[J].生产力研究,2005(3):21 -22.
[3]宋则.流通现代化及流通业竞争力研究[J].商业时代,2006(4):33-35.
[4]王德章,宋德军.流通业促进城市经济发展的实证分析[J].财贸经济,2007(10):98-102.
[5]唐红涛.流通业与区域经济增长的关系探讨——基于面板分析和聚类分析的实证研究[J].天府新论,2009(2):54-58.
[6]张晓峒.计量经济学基础[M].天津:南开大学出版社,2005.

