基于delaunay三角网的三维地形可视化仿真

徐祥龙，李光耀，谭云兰,2，李 超

基于delaunay三角网的三维地形可视化仿真

徐祥龙1，*李光耀1，谭云兰1,2，李 超1

(1. 同济大学CAD研究中心，上海201804；2. 井冈山大学电子与信息工程学院，江西，吉安 343009)

针对在三维地形处理领域中存在的地形数据冗余，可视化处理效率不高，真实感效果不强的问题，提出一种基于delaunay三角网的三维地形生成技术及可视化仿真处理的方法。该方法将DEM数据转化为TIN数据，然后用改进的delaunay算法将TIN数据生成三角网来模拟地形。最后经过纹理映射，光照及渲染，生成具有真实感的三维地形。同时给出了运用VC++和OpenGL实现的三维真实感地形可视化仿真软件。仿真试验表明：该方法能快速的处理地形高程数据，得到了直观的真实感较强的三维地形模型。

Delaunay三角网；三维地形可视化；OpenGL

0 引言

长久以来，人们都是用二维地图来描述地理信息，但在数字化和信息化的今天，随着地理信息应用领域的不断拓展，传统的二维地图已满足不了人们的需求，具有丰富地理信息的三维地形图成为研究热点。

地形可视化是指在计算机上根据数字地形模型(Digital Terrain Model，简称DTM)对地形数据进行三维仿真显示的技术。它涉及到计算机图形学、测绘学、地理信息系统、虚拟现实等诸多学科，并可应用在城市规划、地形勘察、项目选址、路径选取、灾害预测、军事及游戏等各个方面[1]。因此，研究如何更好、更快的实现地形可视化是很有必要的。

本文从地形模拟的角度出发，对地形数据进行处理，应用改进的Delaunay算法建立三维地形模型中的不规则三角网(TIN)，以此来模拟地形表面。并用VC++和OpenGL实现了具有三维真实感的地形可视化仿真软件。

1 数字地形模型的生成

1.1 概述

针对不同的应用目的，人们依据各种数据模型和算法建立了很多种地形可视化模型。对于规则格网RSG(Regular Square Grid): Lindstrom在1996年提出了一种对规则格网表示的地形模型进行实时细节层次删减和绘制的方法[2]；Mark等在1997年提出了“实时优化自适应网格”(Real-Time Optimally Adapting Meshes，简称ROAM)算法[3]。对于不规则三角网TIN(Triangulated Irregular Network): Shamos和Hoey在1975年提出了分割-合并的思想，并证明了在N个离散数据点中建立Delaunay三角网的时间复杂度至少为log[4]。Lawson在1976年提出的逐点插入法思路清晰简单，容易编程实现[5]。徐青等提出了基于TIN的自适应分块算法，把传统的分割­­­­­-合并算法和三角网生长法结合在一起，并给出了相应的地形简化过程[6]。

1.2 数字地形模型(DTM)

数字地形模型(Digit Terrain Model)是地理信息系统中表达空间信息及三维可视化的一种重要模型，构造数字地形模型的方法主要有两类：一是基于规则分布数据点的栅格格网(Grid)；另一个是基于离散数据点的不规则三角网格TIN。它们都有各自的优缺点：规则格网的拓扑关系简单，构造算法比较容易，空间操作及存储方便，但是它的数据冗余较大，难以描述局部复杂地形特征；不规则三角网的优点是数据冗余小，能较好的模拟地形并能描述比较复杂的地形细节，但是它的构造算法比较复杂，空间操作及存储不便。本文主要讨论不规则三角网TIN的构建算法。

构建TIN的算法一般有三种[7]：分而治之算法、数据点逐次插入算法以及三角网生长算法。这些算法都是将数据点连接成网来模拟地形，其效率随着数据点数量的增长呈指数级递减，当数据点数量很大时，效率很低。为了提高TIN的建网效率，本文在研究前人算法的基础上，对Delaunay三角网的建网算法提出了一些改进。

1.3 改进的Delaunay三角网生成算法[8]

改进算法采用逐点内插算法，快速生成Delaunay三角网。因为地形数据块皆为方形，因此可计算出包围矩形作为初始三角网，然后将其余点逐一插入，每插入一个点都用LOP局部优化过程(Local Optimization Procedure)进行优化，保证生成的三角网是Delaunay三角网DTN(Delaunay Triangulated Network )。具体实现过程如下：

（1）遍历所有地形点的坐标，算出所有点的坐标范围，由此得到一个包围所有点的矩形，连接一条矩形对角线，形成初始三角网。

（2）在基本三角网中插入一点P，根据P点坐标调用FindTriangle()函数，找到包含P点的三角形T；

（3）连接P点与三角形T的三个顶点，生成三个新的三角形；

（4）使用LOP算法优化三角网；

（5）重复步骤（2）到（4），直到所有的点都插入完毕。

经过上述步骤，Delaunay三角网已经生成，但算法运行过程中涉及到两个重要函数，分别是FindTriangle()函数和LOP()函数。

FindTriangle()函数：所有的三角形都存储在一个vector容器中，它可以实现随机存取，具有较快的访问速度。每生成一个三角形就加入到这个容器中，因此新生成的三角形都在容器的末尾处。当有新的点插入时，采用从尾至头的顺序查找三角形，有较大几率落在尾部的新三角形中，从而提高查找效率。判断点是否在三角形中可先判断点是否落在包含三角形的矩形内，若在可继续采用向量法判断是否在三角形内部（如图1所示）：

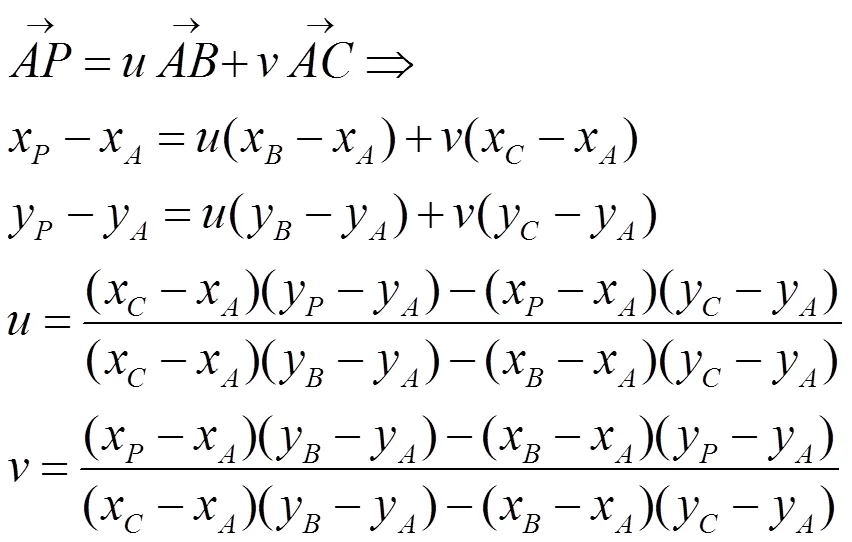
图1 判断点P是否在△ABC中

Fig. 1 If the point P inside the △ABC

LOP()函数：delaunay三角网中每插入一个点都会对当前的三角形进行修改，这个过程称为LOP，可采用如下方法：

连接P点与三角形的三个顶点，生成三个新的三角形，这将导致一些非法边，对每条边执行LOP操作，这样会将这三个三角形变化为delaunay三角形，同时也会影响以P为顶点的其他三角形，应继续对P的对边进行LOP操作，直到所有的三角形都变为delaunay三角形，该算法时间复杂度为(log)[9]。图2为此LOP算法的执行过程：

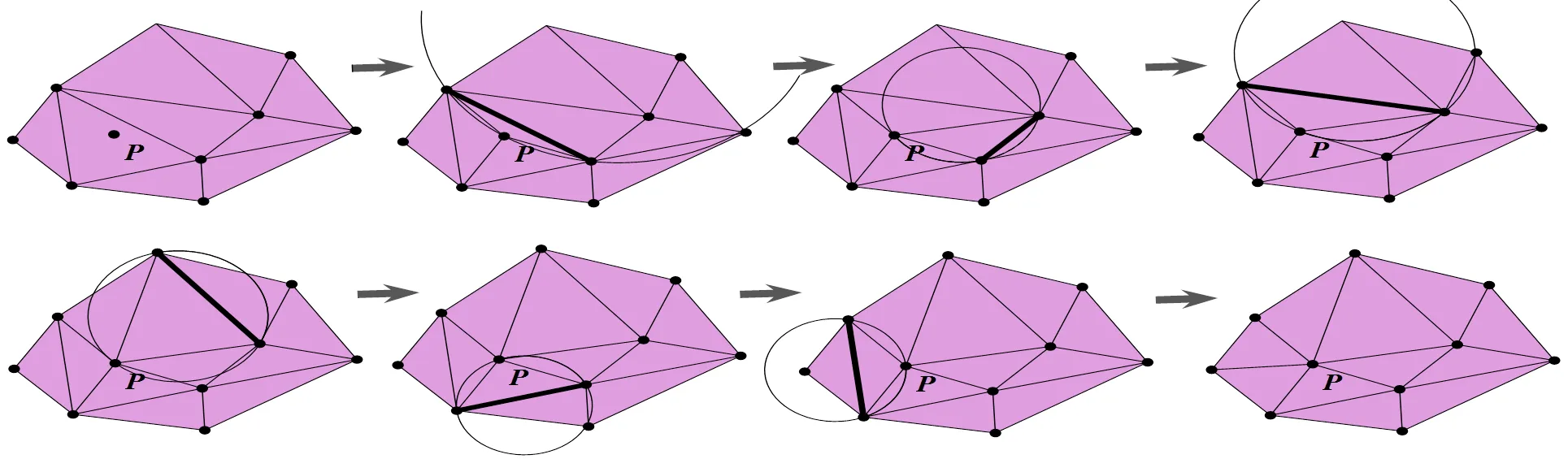
图2 插入点时三角网的优化执行过程

在LOP过程中，每插入一个点至多改变9个三角形[8]，因此算法效率是比较高的。

2 三维真实感地形可视化软件的实现

2.1 三维地形可视化软件的设计

三维地形可视化软件的设计思想是对DEM数据进行处理，按照改进的Delaunay算法生成三角网，来模拟地形表面，然后通过纹理映射、光照及渲染，实现三维真实感地形。根据上述思路，软件的技术路线和流程图如图3所示：

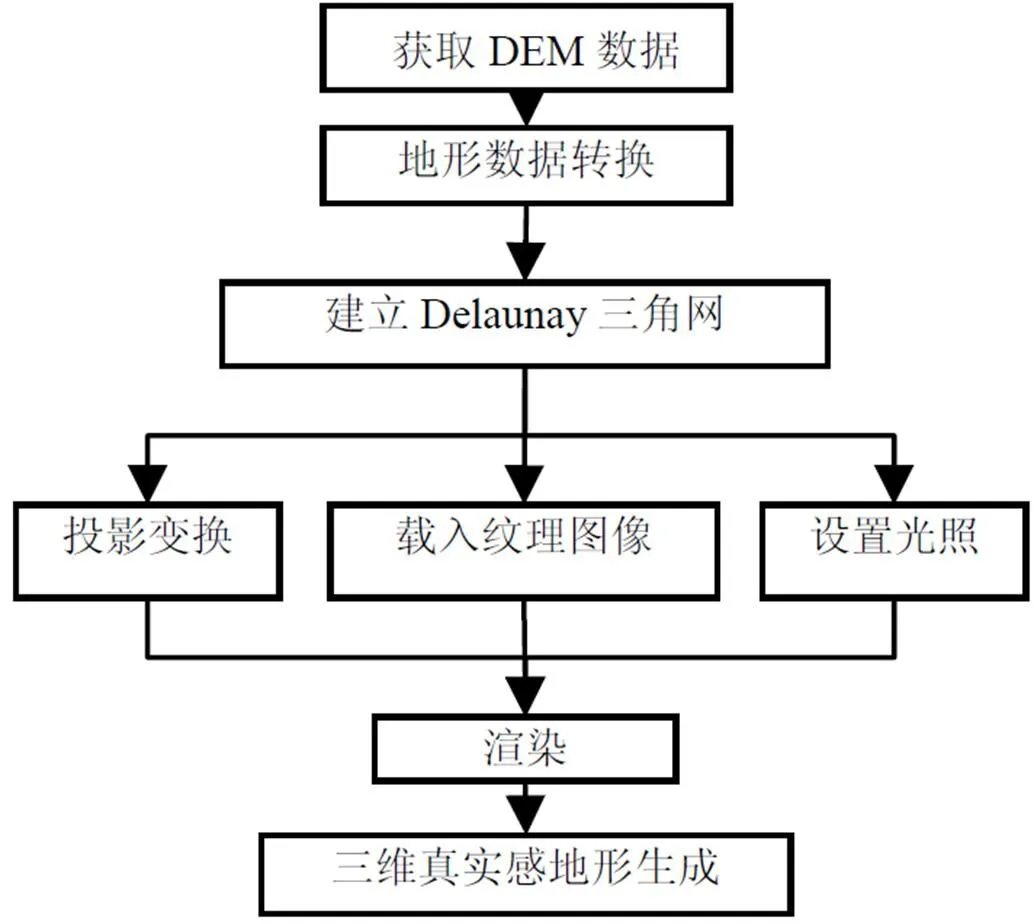
图3 地形建模流程图

2.2 数据结构设计

本三维地形可视化软件在Windows XP操作系统下采用VC++6.0及OpenGL开发，下面是系统中用到的一些关键的数据结构。对三角网中的三角形采用如下数据结构

对于转换DEM数据，系统采用Global Mapper软件来实现，此软件支持各种地形数据的读取和转换，限于篇幅，不再详细介绍。

2.3 实验结果

本实验软件在Windows XP SP3系统平台下使用Visual C ++ 6.0和OpenGL 2.0搭建的软件平台，系统运行的硬件环境：CPU：Intel Core 2 Duo E7300；内存：2G；显卡芯片组：GeForce 9800 GT。使用中国地区的地形数据作为实验数据，实验结果如图4、图5所示：

图4 中国西藏某山区，其中(a)是地形等高线图，(b)是Delaunay三角网图，(c)是经过渲染的三维地形模型

图5 中国浙江某地区，其中(a)是地形等高线图，(b)是Delaunay三角网图，(c)是经过渲染的三维地形模型

上述两地区地形模拟的时间效率如下：

表1 建网的时间效率

3 结论

本文主要针对三维地形显示中的重要环节，用Delaunay三角网模拟地形的部分进行详细描述，并对Delaunay三角网的生成算法进行了改进。从实验结果看来，三维地形建立的效率得到了一定的提高，最后得到了真实感良好的三维地形模型。

[1] 王永明.地形可视化[J].中国图像图形学报.2000.5A(6): 449-456.

[2]Lindstrom P, Koller D, Ribarsky W, et al. Turner. Real-Time Continuous Level of Detail Rendering of Height Fields[C].In:Proceedings of SIGGRAPH'96, 1996.

[3] Mark Duchaineau. ROAMing Tenain:Real-time optimally adap ting meshes[C].In: Proc.Visualization'97, 1997.

[4]Shamos M I, Hoey D. closet-point problems[C]. In: Proceedings of the 16th Annual Symposium on the Foundations of Computer Science, 1975: 151-162.

[5]Lawson C L. Software for c Surface interpolation. Mathematic Soft-ware III, J Rice ED[M]. New York: Academic Press, 1977: 61-194.

[6]徐青．基于自适应分块的TIN三角网生成算法[J]．中国图像图形学报，2000，5(6)：461-465．

[7]徐青.地形三维可视化技术[M].北京:测绘出版社,2000．

[8]贾瑞生,姜岩,孙红梅,等.三维地形建模与可视化研究[J].系统仿真学报,2006,18(1):330-332.

[9]Guibas L J, Knuth D E, Sharir M. Randomized Incremental Construction of Delaunay and Voronoi Diagrams[J]. Algorithmica, 1992(7): 381-413.

Research on 3D Terrain Visualization Based on Delaunay Triangulations Network

XU Xiang-long1，*LI Guang-yao1，TAN Yun-lan1,2，LI Chao1

(1. CAD Research Center of Tongji University, Shanghai 201804,China; 2. School of Electronic Information and Engineering，Jinggangshan University，Ji’an，Jiangxi 343009，China)

Aiming to the problem of data redundancy, low efficiency and not good-enough realistic in 3D terrain processing, we propose a method to generate3D terrain based on Delaunay triangulation. It converts the DEM data to TIN data and generates the triangulation by optimal Delaunay algorithm to model terrain. Finally, we generate high realistic 3D terrain model by texture mapping, lighting and rendering. We also build 3D terrain visualization software using VC++ and OpenGL at the same time. The simulation experiment shows that the method can process the terrain data quickly and get better effect 3D terrain model.

delaunay triangulation; 3D terrain visualization; openGL

TP391.41

A

10.3969/j.issn.1674-8085.2012.02.013

1674-8085(2012)02-0050-04

2012-01-15；

2012-02-22

国家863高技术研究发展计划(2010AA122200)

徐祥龙(1988-)，男，山东临沂人，硕士生，主要从事地形建模与仿真、图形图像处理研究(E-mail: xuxl6125@163.com);

*李光耀(1965-)，男，安徽安庆人，教授，博导，主要从事大规模城市建模与仿真、图形图像处理研究(E-mail: lgy@tongji.edu.cn);

谭云兰(1972-)，女，江西新干人，副教授，同济大学在读博士生，主要从事图像处理，计算机图形与科学可视化研究(E-mail: tanyunlan@163.com);

李 超(1979-)，男，安徽合肥人，博士生，主要从事图像处理，月表地形仿真研究(E-mail: lic321@163.com).