一个半离散非齐次核的逆向Hilbert型不等式
谢子填,陈子明
一个半离散非齐次核的逆向Hilbert型不等式
*谢子填,陈子明
(广东肇庆学院数学与信息科学学院,广东,肇庆 526061)
应用权函数,给出一个带有最佳常数因子的半离散非齐次核的逆向Hilbert型不等式,同时给出他的等价式。



近年来,人们陆续对不等式(1)(2)作了大量推广[2-16]。首先,人们研究了齐次核的,在全平面积分和半离散的Hilbert型不等式,如杨必成[3]给出非齐次核的Hilbert型不等式,谢子填等[13-15]给出实齐次核的Hilbert型不等式,全平面积分的有关论文也都只有些零星结果[9],也基本是零齐次和负齐次的。全平面的离散型和半散离Hilbert型不等式(即使是负数齐次),则至今尚未见到。2011年杨必成教授给出了一个半离散 Hilbert型不等式[2]。
我们应用权函数,将给出一个带有最佳常数因子的半离散非齐次核的逆向Hilbert型不等式,同时给出他的等价式。
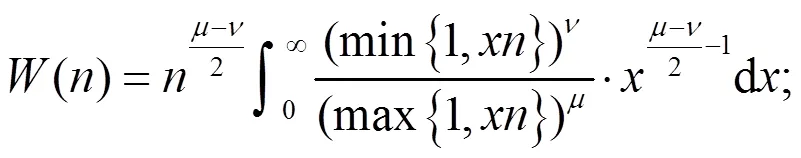
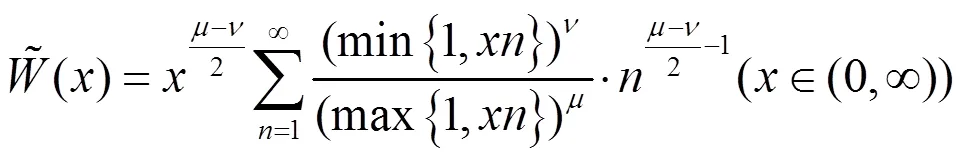
则有
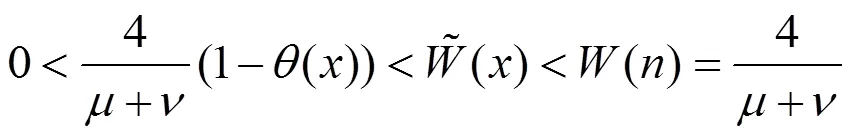
其中
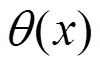
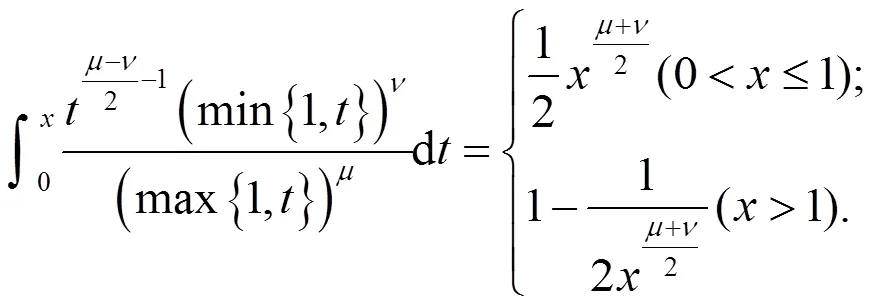
关于严格单调下降,于是
引理获证。
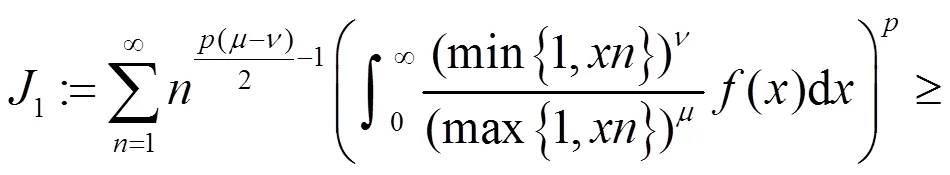
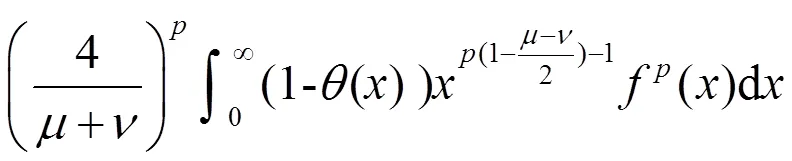
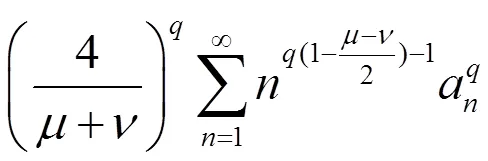
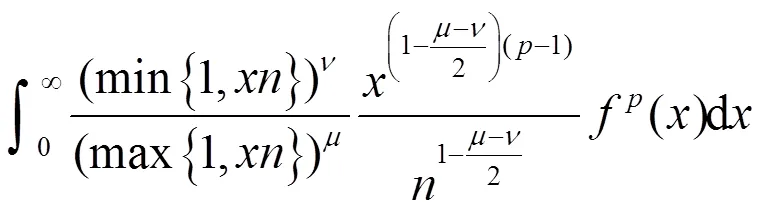
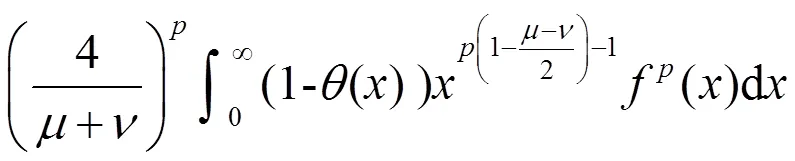
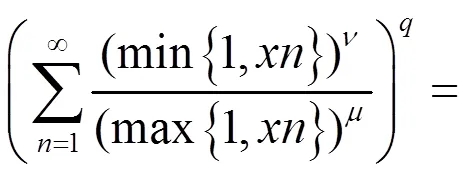
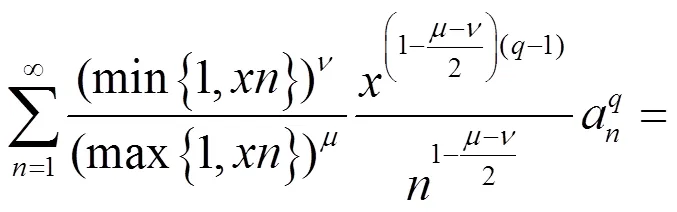
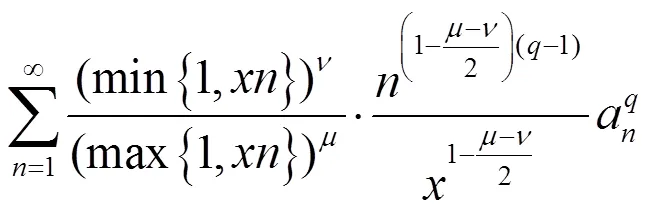
及类似地,
有(9)成立。

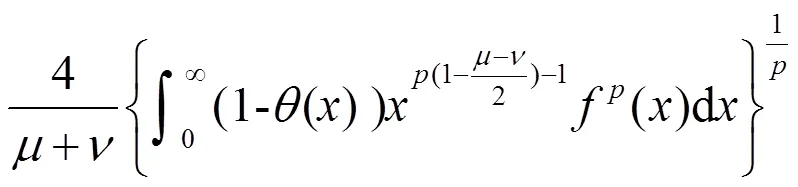
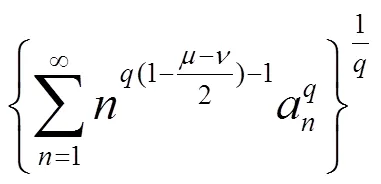
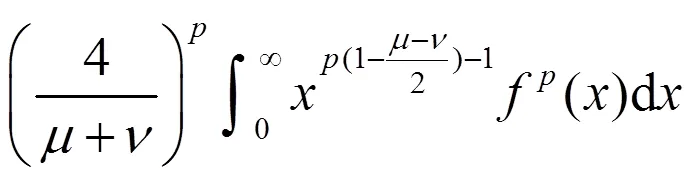
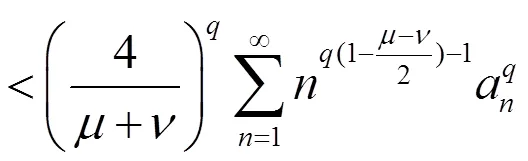

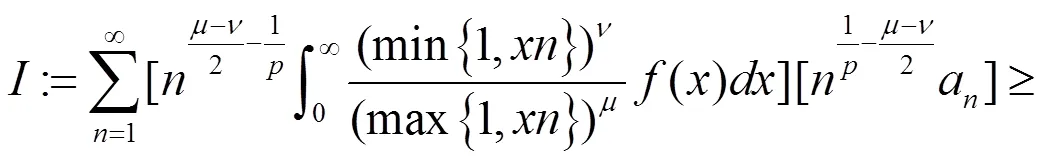
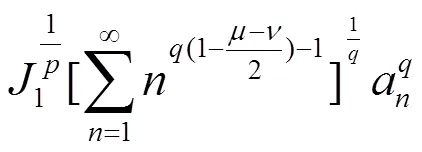
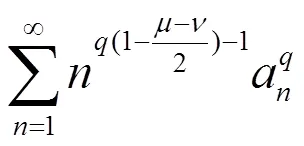
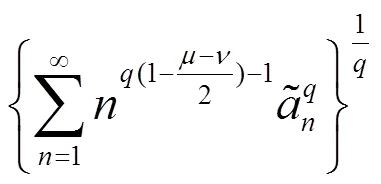
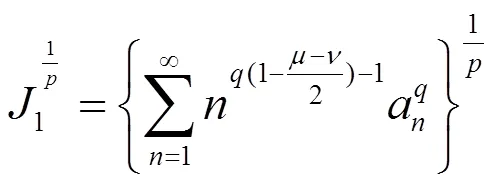
故(12)成立,且与(11)等价。
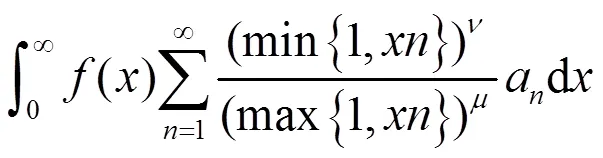
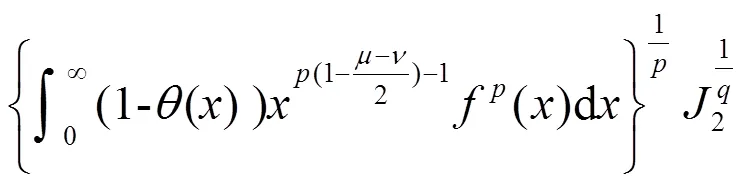
由式(13),有式(11)。
反之,设式(11)成立。取
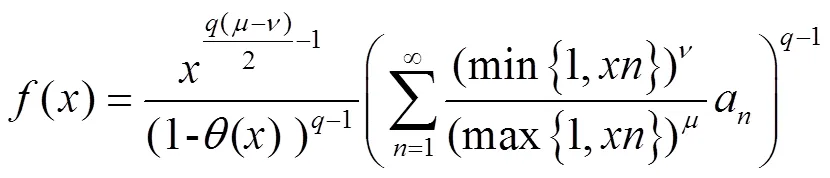
由式(11)有
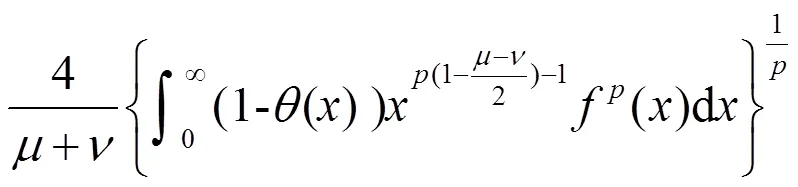
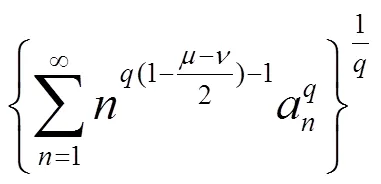
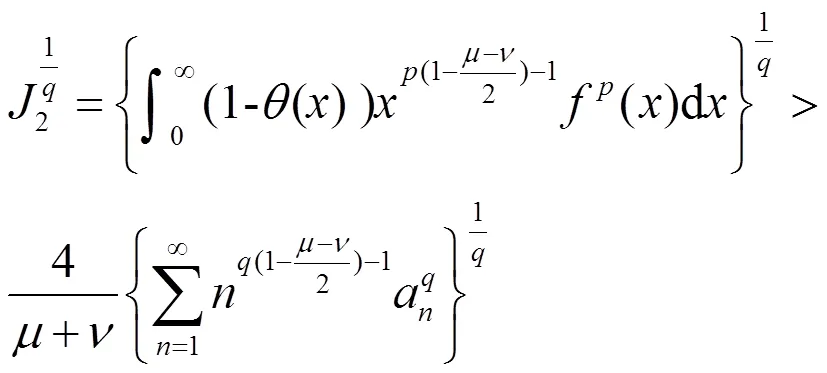
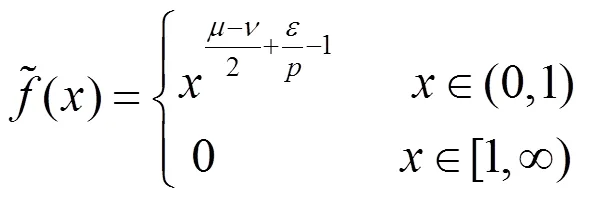
于是
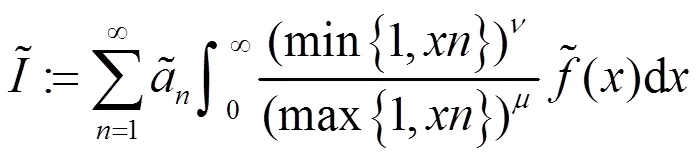
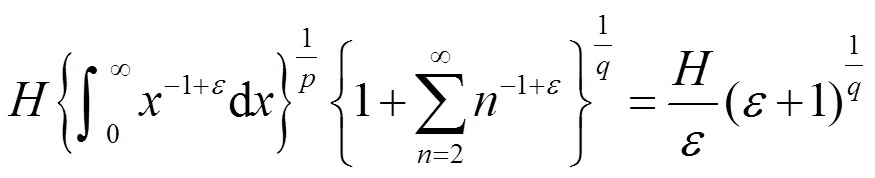
另一方面,又有

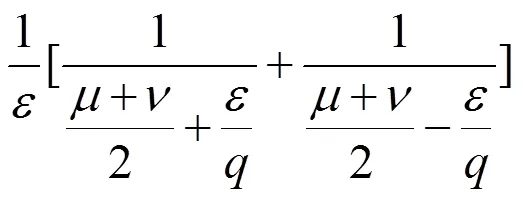
由(18)及(19),有,
注意到(12)(13)和(11)等价,易知式(12)(13)的常数因子也必为最佳值。
[1] Hardy G H. Note on a theorem of Hilbert concerning series of positive term[J].Proc. London Math. Soc. 1925, 23(2) : XLV-XLVI.
[2] 杨必成.一个半离散的Hilbert不等式[J].广东第二师范学院学报,2011,31(3):1-7.
[3] 杨必成.一个推广的非齐次核的Hilbert 型积分不等式[J].吉林大学学报:理学版,2010,48(5):719 -722.
[4] Xie Zitian, Zeng Zheng. A Hilbert-type integral inequality whose kernel is a homogeneous form of degree -3[J].J. Math. Anal. Appl. 2008(339):324-331.
[5] 谢子填, 曾峥.一个新的零齐次核的Hilbert 型积分不等式[J].西南大学学报:自然科学版,2011,23(8):137-141.
[6] 曾峥,谢子填.一个新的有最佳常数因子的 Hilbert型积分不等式[J].华南师范大学学报,2010(3): 31-33.
[7] Zeng Zheng, Xie Zitian. A Hilbert's inequality with a best constant factor, Journal of Inequalities and Applications[J].2009, 820:176-183.
[8] Xie Zitian,Zeng Zheng.A Hilbert-type inequality with some parameters and the integral in whole plane[J].Advances in Pure Mathematics, 2011(1):84-89.
[9] Zheng Zeng, Zitian Xie. On a new Hilbert-type integral inequality with the integral in whole plane[J]. Journal of Inequalities and Applications, 2010, 256:796-803.
[10] Zitian Xie , Zheng Zeng. The Hilbert-type integral inequality with the system kernel of -λ degree homogeneous form[J]. Kyungpook Mathematical Journal, 2010(50):297-306.
[11] Xie Zitian, Zeng Zheng. A Hilbert-type integral inequality with a non-homogeneous form and a best constant factor[J].Advances and Applications in Mathematical Sciens, 2010,3(1) : 61-71.
[12] Xie Zitian. A new reverse Hilbert-type inequality with a best constant Factor[J]. J. Math. Anal. Appl,2008,343:1154-1160.
[13] 谢子填,杨必成,曾峥.一个新的实齐次核的Hilbert 型积分不等式[J].吉林大学学报:理学版,2010,48(6):941-945.
[14] 谢子填, 曾峥.一个实齐次核的Hilbert 型积分不等式及其等价形式[J].浙江大学学报:理学版,2011,38(3) 266-270.
[15] Xie Zitian, Zeng Zheng. On a Hilbert-type integral inequality with the homogeneous kernel of real number-degree and its operator form[J]. Advances and Applications in Mathematical Sciens 2011,10(5)481- 490.
A Half-discrete Reverse Hilbert-type Inequality with a Non-Homogeneous Kernel
*XIE Zi-tian, CHEN Zi-ming
(Dept. of Math. Zhaoqing University, Zhaoqing, Guangdong 526061, China)
Based on the weight function, we give a new half-discrete reverse Hilbert-type inequality of a non-homogeneous kernel with a best constant factor. The equivalent inequality form is considered.
half-discrete; Hilbert-type integral inequality; Holder's inequality
O178
A
10.3969/j.issn.1674-8085.2012.02.002
1674-8085(2012)02-0007-04
2011-12-15;
2012-02-28
*谢子填(1948-),男,广东肇庆人,教授,主要从事解析不等式研究(E-mail: address:gdzqxzt@163.com);
陈子明(1964-),男,广东怀集人,讲师,主要从事高等数学研究(E-mail: zqczm@21cn.com).

