多聚焦图像融合算法

张 攀

0 引言

随着计算机技术、传感器技术以及信息处理技术的不断发展，图像融合作为信息融合的一种强有力的工具，在自动目标识别、军事以及医学图像等领域有着广泛的应用。该技术就是将各种传感器对同一场景，获得的不同源图像在空间和时间上进行配准，利用各图像所含信息优势上的互补性，通过一定的算法获得对同一场景更为清晰、全面、精确的图像描述[1]。

1 粒子群算法

1.1 基本粒子群算法原理

粒子群优化算法的基本原理：设初始化群体规模为M，将种群中每个个体看成搜索空间中的一个微粒，微粒根据自身的飞行经验以及同伴的飞行经验，动态地调整自己在空间中的飞行速度。通过不断的调整粒子的速度与位置，迭代搜索到最优解。在每一次迭代中，粒子往往依靠自身经验和同伴经验进行运动决策。粒子根据自身经验找到的最优解记为pBest个体最优，种群中所有粒子当前经历的最优位置，则称之为gBest全局最优值。

按照粒子的两个最优值，来更新自己的速度与位置，如公式（1）、（2）

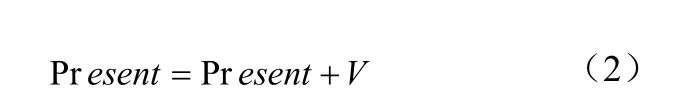
其中，V是粒子的速度，Present代表粒子的当前位置，pBest为个体最优值，gBest为全局最优值，参数c1和c2称为学习因子，通常c1=c2=2，加权系数w一般取值在0.1到0.9之间。通过分析基本粒子群的一些特点，可以知道公式中包含3个部分，分别代表微粒先前的速度、微粒本身的思考以及微粒间的社会信息共享。

粒子不断学习更新自己的位置，最终落到解空间中最优解所在的位置，完成搜索。最后输出全局最优解gBest 。

1.2 基本粒子群算法流程

（1）初始化种群，设群体规模为M。随机初始化各个粒子，包括粒子的随机位置和速度。初始化pBest和gBest的位置。

（2）根据种群粒子的适应度函数计算每个微粒的适应度值。

（3）对每个粒子，将其当前适应值与其个体历史最佳（pBest）对应的适应值作比较。如果当前的适应值更高，则更新为当前历史最优（pBest）。

（4）对每个粒子，将其当前适应值与全局最优对应的适应值（gBest）作比较，如果更好，即当前的适应值更高，则更新粒子群当前全局最优值（gBest）。

（5）更新粒子的速度极其位置，进行种群进化，进化公式根据方程1）和方程（2）。

（6）检查终止条件，（通常为寻找到足够好的解或者达到设定的迭代次数，或者群体最优解停滞不再变化），若满足条件，则结束；否则跳转到步骤（2）。

经典的粒子群优化算法在求解连续空间的优化问题上，能够显示出优良的性能，然而在解决离散问题上，效果就不是很理想了。

2 二进制粒子群算法

在二进制粒子群算法中，每个粒子由一个二进制位串表示，其位置更新过程，如图1所示：

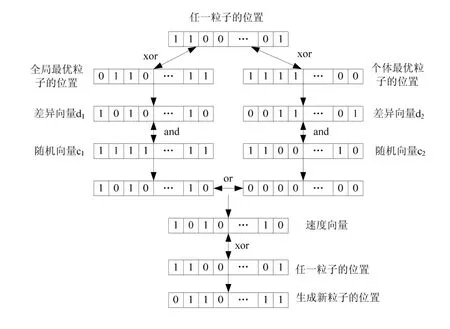
图1 二进制粒子群算法中新粒子的生成过程

任一粒子位置和它的历史最优位置、全局最优位置的差异分别由两个位串表示，称为差异向量，每个位串均有 D个比特位，每一位表示两个位置向量对应元素相同与否，如果相同则该位的值是 0，否则值为 1（Hamming距离）。这一比较过程类似“异或（xor）”运算。然后，随机生成两个不同的向量c1和c2，分别和两个差异向量进行“与（and）”运算。这两个随机二进制位串的作用相当于实值PSO算法中的随机数，为算法增加了探测和开发的能力。速度向量由上一步得到的两个位串进行“或（or）”运算生成。最后，通过将粒子速度向量和位置向量进行“异或（xor）”运算得到新的位置向量[3]。

3 实验结果分析

3.1 灰度图像实验

源图像选择一幅清晰的灰度图像作为标准参考图像，源图像的灰度级别为0～255。分别对源图像进行模糊化处理，生成两幅目标聚焦不同的图像，作为两幅待融合的实验图像，如表1所示：

表1 灰度图像融合数据

BPSO算法比PSO算法表现出明显的速度优势。但两种算法均不能实现完全的重构，究其原因，是群体智能的共同缺陷，在高维复杂空间容易陷入局部极值。

3.2 模糊区域有重叠的多聚焦图像实验

融合数据，如表2所示：

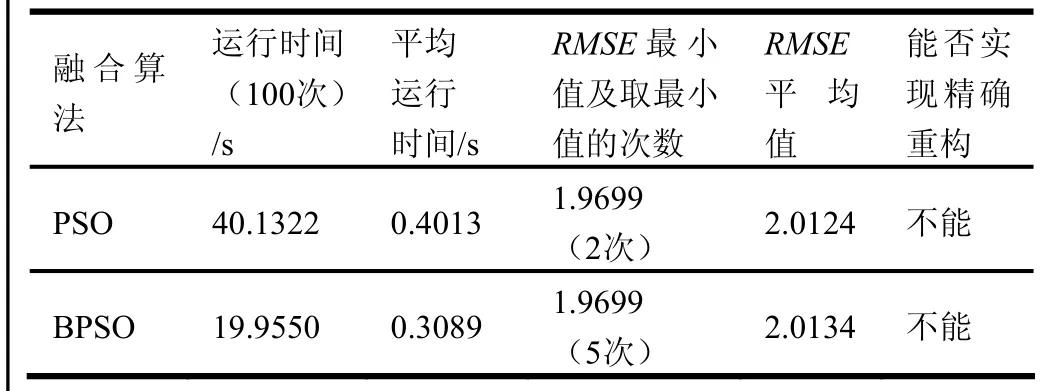
表2 聚焦目标有重叠模糊区域的多聚焦图像融合数据

实验中 RMSE的最小值没有等于零的情况，这说明聚焦目标有重叠模糊区域的多聚焦图像是无法实现精确重构的，两种算法中 RMSE的最小值均为 1.9699，这说明RMSE=1.9699就是最好的融合效果了

3.3 多聚焦非配准图像

如图2（a）和（b）所示：

图2 （a）

图2 （b）

数字相机摄取的一对多聚焦图像，大小为256×256，其中一幅图像中，聚焦点在钟表上，而另一幅图像聚焦点在书架上。

我们分别采用两种群智能优化的融合算法对两幅待融合的多聚焦灰度图像进行融合实验。

图2 多聚焦非配准图像

显而易见，图2（d）、（e）这2幅融合图像明显优于（c）图，因为图 2（c）图上带有很多噪声。因此通过两种算法的图像融合方法所获得的图像要比单纯采用数字相机自动聚焦方法所得到的图像质量高得多。

4 结束语

粒子群算法通过群体中个体之间的协作来寻找最优解。粒子群进化的一个显著优势，就是在群体中各粒子存在着信息共享，使整个群体的运动在问题求解空间中，产生从无序到有序的演化过程，从而获取最优解。由于粒子群算法具有简单的计算形式和参数设置、良好的收敛性能等优点，在各类优化问题研究领域，显示出了相当的潜力。

[1]李树涛，王耀南，张昌凡.基于视觉特性的多聚焦图像融合[J].电子学报.2001，12 1699～1701.

[2]梁军.粒子群优化算法在最优化问题中的研究.[D]广西师范大学.2008.

[3]吴启迪，汪镭.智能微粒群算法研究及应用.江苏：[M]江苏教育出版社，2005.

[4]焦李成，公茂果，王爽等.自然计算、机器学习与图像理解前沿[M].陕西：西安电子科技大学出版社，2008.

[5]Karathanassi V, Kolokousis P, Ioannidou S.A comparison study on fusion methods using evaluation indicators[J].International journal of remote sensing, 2007,28(10):2309～2341.