基于EMD与三阶累积量的水声瞬态信号检测

何光进，程锦房，许 杰，李 楠，张 炜

(海军工程大学 兵器工程系，湖北 武汉 430033)

0 引言

水下目标在航行时发生的噪声可以分成2类:一类是连续重复产生的，另一类是瞬态变化的。随着隐身技术的发展，水下目标的辐射噪声越来越低，无源检测和识别水下目标越来越困难。潜艇、鱼雷等目标由于机械设备的运行状态、工况等变化，不可避免地会发出瞬态信号，利用这些突发性的瞬态信号，则可发现目标甚至识别目标［1］。但由于瞬态信号的突发性和强烈的不稳定性，设计1个宽容性的检测器非常困难，特别是对水下复杂背景环境下瞬态信号的检测和识别。近年来，该项研究受到了国内外学者的重视，美国NUWC设立了多项相关研究课题，研究成果在多篇文献中均有体现［2］。国内学者王燕麟、吴国清、邢军等均对水声瞬态信号的检测进行了相关的研究，方法有双谱能量检测和短时谱分析等。

现有的瞬态信号检测方法在干扰有色噪声时检测性能都将受到很大影响，文献［3－5］提出了将检测到的信号通过一滤波器组，使信号在频域上分离，选择输出能量较大的1组子频带信号近似给出信号的时频描述。该方法需要预先设计好1组满足重构条件的滤波器。本文运用EMD方法的滤波器特性，取代滤波器组对采集到的信号进行降噪处理，选择能量较大的几组IMF进行高阶累积量分析，计算其三阶累积量对角切片的短时估计并构造检测统计量。最后根据检测统计量的包络特性判断有无目标信号存在。

1 EMD与三阶累积量

EMD方法是由美国华裔科学家N.Huang提出的一种处理非线性、非平稳信号的分析方法［6］。这一方法创造性地提出了本征模态函数(Intrinsic Mode Function，IMF)概念以及将任意信号分解为多个IMF的方法，即EMD方法。任何复杂信号都可以经过一定的步骤分解成有限个IMF的和，且各个IMF分量信号都是平稳的窄带信号。对于高斯白噪声，EMD相当于1组窄带滤波器，EMD对数据处理相当于对数据进行二值滤波［7］，EMD的滤波器特性如图1所示。本文正是运用EMD的滤波器来将信号在频域内进行分离。

图1 EMD的滤波器特性Fig.1 The filter characters of EMD

高阶累积量方法因其对多种噪声都有很好的抑制作用逐渐成为信号处理的新热点，是近年来发展较快的现代信号处理方法之一。它不仅对未知自相关的加性噪声不敏感，而且对另外一类非歪斜的非高斯有色噪声(如均匀分布和任何对称分布噪声)也不敏感，因此在非高斯性、非线性、非因果性、非最小相位、非平稳性、高斯有色噪声或盲信号处理中发挥了重要的作用。三阶累积量及其对角切片的计算方法参见文献［8］。

2 检测方法

基于EMD的三阶累积量检测过程为:首先将检测信号进行EMD滤波处理，对信号在频域上进行分离，选择能量较大的1组子频带信号近似给出信号的时频描述，然后在各个选中的子频带内单独计算三阶累积量对角切片的短时估计，抑制各个子频带内的噪声，通过构造的检测函数给出信号的特征包络，具体步骤如下:

1)计算经EMD滤波后各IMF分量的能量，选取能量较大的1组IMF并进行时频分析;

2)对选择的IMF分量zi(n)求其三阶累积量对角切片的短时估计［9］:

其中，

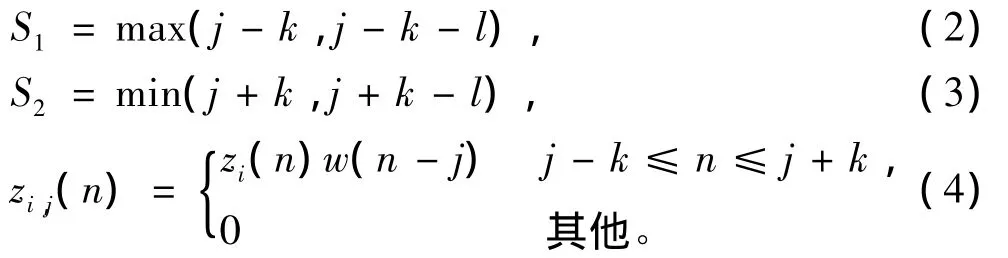
而w(n)是长度为2k+1的窗函数，经分析比较，此处选择汉明窗，即

做为检测函数，检测结果可给出瞬态信号的到达时间和波形包络，从而完成信号特征的检测。检测过程的流程图如图2所示。

图2 检测流程图Fig.2 The flowchart of detection

3 仿真分析

为检测本文提出的检测方法的有效性，用以下模型仿真水声瞬态信号［10］:

式中，取a=100，b=1 000，频率f=400，抽样频率为1 024，得到信号的波形如图3和图4所示。以信噪比－15 dB将其与高斯白噪声混合，混合后的波形如图5和图6所示。从图中可以看出，无论在时域或频域都分辨不出信号。

将合成信号进行EMD分解，得到的10个IMF分量，运用文献［11］给出的方法计算各个IMF分量的能量，得到如图7所示的结果。

从图7中可以看出，信号的能量主要集中在高频段，IMF1的能量占了全部能量的77.19%。只要对IMF1分量进行时频描述，如图8和图9所示。从图9可看出，频率为400 Hz的信号部分也主要集中在IMF1中。

根据式(1)计算三阶累积量对角切片的短时估计，根据式(2)计算检测函数，如图10所示，其频谱如图11所示。对检测函数进行包络检波，得到的信号的上包络如图12所示。从图中可以看出，经过EMD滤波和三阶累积量对角切片处理后的信号抑制了大部高斯噪声的影响，粗略地给出了瞬态信号出现的时刻在100/1024=0.1 s左右，信号的频率范围在400 Hz附近。

4 结语

本文用EMD方法取代了传统的滤波器组方法，避免了设计可重构的滤波器组，降低了工程实现的复杂性。运用EMD方法自适应地将信号在频域内分离成一系列的IMF分量，根据能量法选择信号占主导地位的IMF模态并求得其三阶累积量对角切片的短时估计，构造检测函数，利用检测函数的包络作为检测信号的标准。通过仿真数据表明本文提出的方法能在较低信噪比下检测出目标信号的出现时刻和目标频率，具有一定的工程应用价值。

［1］邢军，刘忠.非高斯水声瞬态信号双通道Power-Law检测［J］.声学技术，2008，27(1):126 －130.XING Jun，LIU Zhong.Non-Gaussian underwater acoustic transient signals detection with dual-channel using Power-Law detectors［J］.Technical Acoustics，2009，27(1):126－130.

［2］吕俊军，吴国清，杜波.非高斯水声瞬态信号Power-Law检测［J］.声学学报，2004，29(4):359 －362.LU Jun-jun， WU Guo-qing， DU Bo. Non-Gaussian underwater transient signals detection using power-law detector［J］.Acta Acustica，2004，29(4):359 －362.

［3］范虹，孟庆丰，张优云，等.基于三阶累积量对角切片的信号特征检测［J］.计算机工程与应用，2006，(36):7 －8.FAN Hong，MENG Qing － feng，ZHANG You － yun，et al.Signal feature detection based on third order cumulant diagonal slice［J］. Computer Engineering and Applications，2006，(36):7 －8.

［4］FAROOK S，GORAN S.On detection using filter banks and higher order statistics［J］.IEEE Transactions on Aerospace and Electronic System，2000，36(4):1179 －1189.

［5］戴幻尧，蒋鸿宇.基于滤波器组和高阶累积量技术的LPI信号特征检测的新方法［J］.系统工程与电子技术，2009，31(6):1336 －1340.DAI Huan-yao，JIANG Hong-yu.Research on LPI signals feature detection based on parallel filter bank and higher order cumulants［J］.Systems Engineering and Electronics，2009，31(6):1336 －1340.

［6］HUANGN E，SHEN Z.The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis:Procedure Report［R］.London:1998，serial.A454:903 －995.

［7］FLANDRIN P，RILLING G，GONCALVES P.Empirical mode decomposition as a filter bank［J］.IEEE Signal Processing Letters，2003，11(2):1 －4.

［8］张贤达.现代信号处理(第二版)［M］.北京:清华大学出版社，2002.

［9］柯永发，陈永光，张哲峰.基于四阶累积量对角切片的短波自适应通信信号检测［J］.电子学报，2006，34(3):419－423.KE Yong-fa，CHEN Yong-guang，ZHANG Zhe-feng.HF adaptive radio communication signal detection based on fourth-oOrder cumulants diagonal slice［J］. Acta Electronica Sinica，2006，34(3):419 －423.

［10］吴国清，陈永强，李乐强，等.水声瞬态信号短时谱形态及谱相关法检测［J］.声学学报，2000，25(6):510－515.WU Guo-qing，CHEN Yong-qiang，LI Le-qiang，et al.The analysis of underwater transient signal and their detection by spectral correlation［J］.Acta Acustica，2000，25(6):510－515.

［11］BOUDRAA A O，CEXUS J C，et al.Noise filtering using empirical mode decomposition［J］.IEEE Xplore Gigital Librarg，2007，(12 －15):1 －4.