船舶推进轴系冲击响应计算方法

韩江桂，吴新跃，贺少华

(海军工程大学船舶与动力学院，湖北武汉430033)

0 引言

船舶在重载、逆风、污底、斜水流航行时，轴系会受到较大的推力。轴系承受的扭矩在轴系中产生扭应力，而推力将会产生压应力。除此之外，轴系和螺旋桨本身的重量以及其他附件的作用，使轴系产生弯曲应力;安装误差、船体变形、轴系的扭转振动、横向振动、纵向振动以及螺旋桨的不均匀水动力作用等都会在轴系中产生附加应力。上述诸力和力矩往往是周期变化的，这就更增加了它们的危险性。由此可见，轴系的工作条件很差，往往会出现损伤，严重时甚至断裂。船舶推进轴系还可能会遭受到接触性爆炸、水下非接触性爆炸、自身武器发射时的反冲力等冲击载荷的作用，将不可避免产生振动。在船舶设备冲击等级里，推进系统为A级设备(结构、系统)，即对完成必要战斗任务起直接和关键支撑作用的设备，在美海军军标NAVSEA 0908 －LP －000 －3010(Rev.1)［1］中，规定了一些典型关键部位(部件)，这些部位(部件)通常都被军方要求建造部门利用动态设计分析方法(DDAM)进行冲击评估，它包括舵和舵柄、推进轴系(不包括螺旋桨)、主减速齿轮箱、桅杆(天线)等。由于涉及到军事机密，国外对于船舶设备的抗冲研究很少有公开的文献。国内一些学者做过这方面工作，沈荣瀛等［2］以3组挠性弹簧钢板支撑的3个轴承座分别模拟尾轴承、中间轴承和推力轴承，设计、制作了轴系试验模型，进行了轴系固有频率测试和冲击试验研究。汪玉等［3－4］将轴承座处理成弹性约束的边界，采用有限元方法导出了轴承支承处冲击应力计算公式。周瑞平［5］建立了尾管轴承的非线性模型，计算了考虑轴承油膜刚度的轴系校正。

1 DDAM和GJB1060.1－91中的冲击动力学分析方法

使用GJB1060.1－91［6］中的冲击动力学分析方法进行冲击响应计算有2个必要的前提:一是固定基础固有频率必须在5 Hz以上，这是因为频率过低时，加速度和速度冲击谱不适合使用;二是不存在密集模态，密集模态有可能严重放大计算结果。虽然美国海军DDAM修订版对密集模态已经提出了解决的方法，但该方法目前只适合简单对象的理论解析计算，还没有应用在有限元方法计算中。目前的商业有限元软件如Nastran中的DDAM模块还无法解决密集模态问题。

经计算(DDAM模型如图3所示)，该船尾轴系存在着大量的密集模态，各模型一般都有二阶以上低频模态频率小于5 Hz，因而不适合采用DDAM进行冲击响应计算。

实际上，在 NAVSEA0908－LP－000－3010(Rev.1)和最近几届振动与冲击分会上都已经提到DDAM不适合这样大跨度推进轴系。除上述提到的原因外，还因为对于一个给定的设备来说，DDAM假定其固定基础处的冲击输入是处处相同的(虽然DDAM对不同的安装位置给予了区分)，所以它不适合基础跨度大的设备。此时最好的办法是建模时将设备基础处的部分船舶结构考虑进来，将固定基础向下游移动，然后，在冲击实船爆炸试验中现场测得固定基础不同位置的时间历程冲击激励，然后采用时域的办法进行解算。基于DDAM(包括GJB1060.1－91中的冲击动力学分析方法)的不足，可考虑采用时域方法进行该型推进轴系的冲击响应计算。本文即采用德国海军BV0430［7］标准对推进轴系的部分轴段进行冲击响应计算。计算是在时域的范围内进行的，它可以克服DDAM的上述大部分弊端，但仍然保留了固定基础激励处处相同的假设。

2 时域计算冲击激励施加方法及瞬态响应算法

2.1 冲击激励施加方法

建立如图1所示的三自由度系统，基础加速度运动冲击激励u˙˙(t)为:

图1 三质量系统基础冲击模型Fig.1 Impact model based on the three mass systems

令y(t)=x(t)－u，则有:

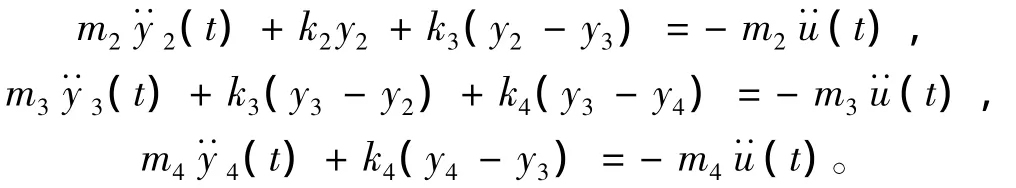
从上述基础冲击激励下系统的动力学方程可以看出，基础加速度冲击激励实际上等效于施加在各质量点上。求解上式即可得到各质量点的位移、速度和加速度响应时间历程。而系统应力即弹簧弹性力为k2y2，k3(y3－y2)和k4(y3－y4)。所以作者认为，基础加速度运动激励实际上是施加在系统各质量点上，而系统在界面与激发平台固接。进而延伸到有限元离散系统中，如用Ansys软件进行瞬态响应计算时，基础加速度运动冲击激励施加在Global单元即所有单元体上，而系统在固定基础处6个自由度全约束。

2.2 瞬态响应算法

在Ansys11.0瞬态响应计算模块中，通过多载荷步施加时间历程加速度冲击激励，采用Newmark迭代算法计算时域响应，Newmark直接积分方法无条件稳定，在瞬态响应计算中最为常用。存储均匀时间间隔的子步数的单元和节点位移、加速度和Von Mises应力，在后处理模块中显示结果并进行分析。

Newmark迭代算法基本公式为:

式中:γ和β为Newmark常数，表示对高阶小量的修正。γ，β取不同值可以得到多种关系式，当γ=1/2、β=1/4即为平均加速度法;β=0为常加速度法(中心差分法);β=1/6为线性加速度法。可证，对线性系统，γ≥1/2和β≥1/2为无条件稳定。β数值的增加将降低计算精度，β=1/12计算精度最高，但属于条件稳定。Newmark指出，对于线性系统γ＜1/2将产生负阻尼，即在积分计算中导致振幅的增长，而当γ＞1/2将产生人工阻尼，从而使振幅人为的衰减，故一般采用γ≥1/2，最常用的是取γ=1/2，再变动β，故通常称为Newmark－β法。如果令γ=1，β=0.5，即得For-Euler法。

2.3 冲击设计输入加速度时间历程曲线的确定

计算得到冲击设计输入激励为组合双三角波加速度时间历程，曲线如图2所示。

图2 BV0430冲击规范组合双三角波时间历程Fig.2 Two-time history of the triangular wave of BV0430 impact specification combination

3 BV0430标准

标准冲击输入中组合三角波的具体计算公式见表1。

表1 BV0430标准冲击输入具体公式Tab.1 Specific formula of impact input on BV0430 standard

该标准规定的设计冲击谱适用于重量50 t以下的设备。标准冲击谱还应根据设备的重量进行调整，可根据下列公式确定冲击载荷缩减系数Aa0和Av0。

当设备重量＞5 t时，冲击响应值:

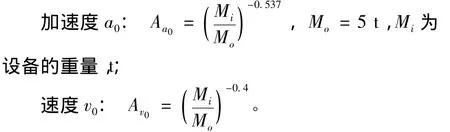
4 抗冲击性能分析

4.1 中间轴段(内)抗冲击性能分析

首先建立了中间轴段(内)的DDAM模型，冲击动力学模型同DDAM模型，根据冲击动力学模型再进行响应分析计算，DDAM模型如图3所示。

图3 (内)轴段分段有限元模型Fig.3 Finite element model of the subsection in shaft(inner)

根据BV0430标准，中间轴段的质量为19.542 t，冲击缩减系数为:

根据标准计算公式，代人冲击缩减系数，根据表1公式可计算出垂直方向、左右舷方向的组合三角波相关参数，这里仅给出垂直方向结果。

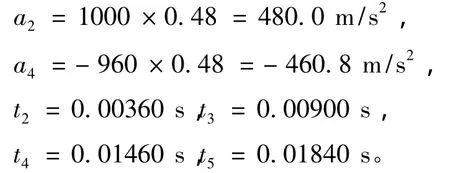
4.2 计算结果分析

计算得到最大应力481 MPa，最大变形28 mm，位于沿首尾方向第2个法兰连接处(螺栓孔内)，如图4和图5所示。应力最大值出现在冲击持续时间之外，即残余响应大于主响应，如图6所示。

图4 中间轴段瞬时应力分布Fig.4 Distribution of instantaneous stress on intermediate shaft

在轴承计算中本文引入接触效应，将工作轴颈和轴承建立接触的关系。所有的接触问题都需要定义接触刚度，2个表面之间渗透量的大小取决了接触刚度，过大的接触刚度可能会引起总刚矩阵的病态，而造成收敛困难。一般来说，应该选取足够大的接触刚度以保证接触渗透小到可以接受，但同时又应该让接触刚度足够小以使不会引起总刚矩阵的病态问题而保证收敛性。Ansys程序会根据变形体单元的材料特性来估计一个缺省的接触刚度值，用实常数FKN来为接触刚度指定1个比例因子或指定1个真正的值，比例因子一般在0.01和10之间，当避免过多的迭代次数时，应该尽量使渗透达到极小值。

为了取得1个较好的接触刚度值，可采用的方法有以下3种:

1)试用不同的值直到找到正确的值。也就是刚开始使用1个较小的值，然后稳步的增加直到分析的结果不再有什么变化。那么对于某一特定分析的问题，这一点就是需要的合适值。

2)开始时取1个较低的值，低估取值要比高估好，因为由1个较低的接触刚度导致的渗透问题要比过高的接触刚度导致的收敛性困难，要容易解决;对前几个子步进行计算;检查渗透量和每一子步中的平衡迭代次数，如果总体收敛困难是由过大的渗透引起的(而不是由不平衡力和位移增量引起的)，那么可能低估了FKN的值或者是将FTOLN的值取得太小，如果总体的收敛困难是由于不平衡力和位移增量达到收敛值需要过多的迭代次数，而不是由于过大的渗透量，那么FKN的值可能被高估;按需要调整FKN或FTOLN的值，重新分析。

3)采用Ansys软件提供的默认值。当采用第3种方法遇到不收敛和结果明显有偏差值，结合第1和第2种方法调整接触刚度，直到计算结果尽量可信为止。应用基础刚度计算的轴瓦瞬时应力分布如图7所示，最大应力位于沿首尾方向第3个中间轴承下轴瓦边沿位置与上轴瓦相邻处。

图7 轴瓦瞬时应力分布Fig.7 Distribution of instantaneous stress of sleeve

5 结语

1)通过分析得到:该中间轴系不适合采用DDAM和GJB1060.1－91冲击动力学分析方法进行冲击响应计算。

2)根据图4～图6，在这些螺栓连接处冲击应力过大，在下一步研究中需要建立真实螺栓的有限元模型，对连接螺栓进行详细的冲击响应计算分析。

3)根据图7，轴承应力较大值集中在轴瓦的两端和上下轴瓦的结合处，下轴瓦的冲击应力响应大于上轴瓦，应力最大值已超过了许用应力值标准;轴承的接触计算较成功，收敛性好，渗透量小，计算结果的整体趋势符合工程经验。

4)如果能实场测得轴系基础各处的实际冲击激励时间历程，则可以整体计算轴系响应，而可以不采用本文将长轴整体分割成几个部分分别建模计算的方法。

5)有限元仿真计算准确度与计算所要付出的代价成正比。对于本文的“冲击动力学计算”，计算结果能否反映客观实际，除与建模方法、算法精度等有关外，还主要受研究对象模型完备性的影响。研究所采用的方法和相关的知识、理论是正确的，如果条件允许，在下一步的研究中理论上可以进行任意深度的细化研究。

［1］Shock Design Criteria for Surface Ships［S］，NAVSEA 0908－LP －000 －3010(REV.1)，1995.

［2］孙洪军，沈荣瀛，沈密群，等.船舶推进轴系冲击特性试验研究［J］.船舶工程，2006，28(6):20 －22.SUN Hong-jun，SHEN Rong-ying，SHEN Mi-qun，et al.Experimetalstudy on shock performance ofmarine propulsive shafting［J］.Ship Engineering，2006，28(6):20－22.

［3］汪玉，沈荣瀛，张智勇.船舶推进轴系冲击响应［J］.中国造船，2000，41(3):74 －79.WANG Yu，SHEN Rong-ying，ZHANG Zhi-yong.Shock response of propulsive shaft of vessels［J］.Shipbuilding of China，2000，41(3):74 －79.

［4］汪玉，赵建华，杜俭业，等.基于多体动力学有限元计算的一种舰用柴油机抗冲击性能仿真［J］.振动与冲击，2009，28(11):87 －90，129.WANG Yu，ZHAO Jian-hua，DU Jian-ye，et al.Simulation on antishock performance of a marine diesel engine by using finite elementcalculation based on multibody dynamics［J］.Journal of Vibration and Shock，2009，28(11):87 －90，129.

［5］周瑞平.超大型船舶推进轴系校中理论研究［D］.武汉:武汉理工大学，2006.ZHOU Rui-ping.Research on adjusting theory of super propulsive shafting in ship［D］.Wuhan:Wuhan University of Technology，2006.

［6］国防科学技术工业委员会.舰船环境条件要求机械环境［S］，GJB1060.1 －91，1991.National Science and Technology Industry Committee.Ships environmental conditions［S］，GJB1060.1 － 91，1991.

［7］联邦德国海军.冲击安全性［S］，BV0430，1985.The Navy of Germany.The impact safety［S］，BV0430，1985.