水面舰船船型选型评估方法
张 恒,杨 屹
(海军装备研究院,北京100061)
0 引言
未来信息化战争对水面舰船平台性能要求越来越高,而目前水面舰船大多采用常规单体船型,要进一步提高常规单体船型的综合性能满足不同类型舰船的需求存在困难,为此,世界海军强国先后研发了多种新船型,如小水线面双体船、穿浪双体船、深V船型、三体船、各类复合船型等。各类新船型具有其自身独特的性能特点,如在快速性、耐波性、装载能力、总布置等方面优于常规单体船型,因而,新船型逐渐在水面舰船中得到应用,如美国“独立”号濒海战舰采用的三体船型等。同时,新船型其独特的船体构型也可能在某些性能方面存在劣势。因此,在水面舰艇论证阶段船型方案选型决策时,需要建立合理的评估指标体系和定量的综合评估方法,通过综合权衡、科学评估,为船型选型决策提供依据。
目前,在水面舰船船型方案选型时,多是针对某些性能如适航性、总布置等方面单项对比分析,未采用定量的综合评估方法,分析结果不能全面反映出各船型综合性能的优劣。本文提出船型选型定量评估流程,建立综合性能评估指标体系,基于层次分析法和灰色关联度理论建立船型选型综合评估方法,通过一船型平台选型实例验证所提方法的可行性。
1 水面舰船船型选型综合评估流程
水面舰船选型决策中,首先根据使用需求确定所需考虑的主要性能指标,构建指标层次结构,建立评估指标体系。
在建立评估指标体系的基础上,需要确定各底层指标值的计算获取方法,由于各种船型特点的不同,因此需要针对不同船型选择适用的计算方法。
最后,建立综合评估方法,包括各层指标权重的计算方法和指标的综合归一评估方法。主要流程见图1。

图1 综合评估流程Fig.1 The process of integrated evaluation
2 建立评估指标体系
船型选型评估是一个对多目标、多因素系统进行综合评估的过程,建立评估指标体系的一般原则对其基本适用,因此,建立指标体系需要遵循完备性、一致性、独立性、简洁性、可测性、可比性等原则[1]。
建立指标体系的过程如下:首先明确所应用舰船平台的主要作战使用要求以及对平台性能的需求,当确定了评估的目标与需求后,接下来进一步明确它们的外延和内涵,并对其进行分解细化,最后能够用一系列相关属性来描述它们,这些属性就是评估因素。接下来需要对评估因素进行进一步处理和筛选,形成指标集。确定指标集后,依据指标体系建立原则,按任务目标和性能分类,明确指标的层次结构,完成指标体系的建立,如图2所示。

图2 指标体系建立过程Fig.2 The process of establish the index
新船型船型特点各异,各种船型相对常规船型均有其优点,但也有其缺陷,在新型舰船平台选型时,对性能综合评估主要从以下几方面进行考察。
1)机动性能。指在一定条件下部署到或撤离一定海区和在某一条件下机动规避危险的能力,包括快速性、耐波性、操纵性等方面。
2)舰船静力性能。包括浮性、稳性、不沉性几方面,它是关系到舰船航行安全性的重要因素。
3)总布置和装载能力。反映该船型对电子武备、机电设备等的布置能力,以及有效装载能力。
水面舰船船型选型评估指标体系如图3所示。
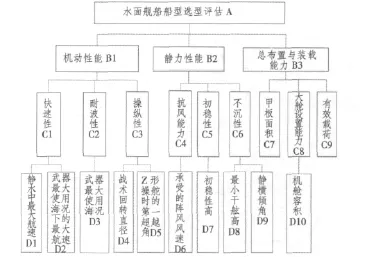
图3 水面舰船船型选型评估指标体系Fig.3 The process of establish the index
3 确定指标计算方法
各类新船型由于船型特点各异,其水动力性能和常规单体船型存在一定差异,目前水面舰船船型选型中主要考虑常规单体船型、双体船型、三体船型等。针对这几种船型分别确定其水动力性能计算方法如下:
1)快速性预报方法
目前,在船舶阻力性能计算研究中逐步发展了基于势流理论的兴波理论方法和基于CFD技术的船舶粘性绕流计算方法来预报船舶阻力性能。在势流理论中,基于改进的 Noblesse新细长船理论[2]、Michell线性理论[3]、改进的 Dawson 方法[4]均被用于计算单体、双体、三体船型的兴波阻力性能,进而预报其全船阻力性能。由于基于势流理论的阻力性能计算方法比粘性绕流计算方法计算时间短,计算方法也较成熟,因此在船型方案选型中可选用以上几种势流理论方法预报兴波阻力。
2)耐波性预报方法
目前,在单体船的耐波性预报中,二维切片法已达到工程应用的精度。然而,采用切片理论对高速双体船、三体船进行运动预报时遇到了困难,不仅是由于切片法对航速的限制,还有片体之间水动力干扰引起的伪共振问题。为解决这个问题,人们提出了在切片法中引入修正系数[5]、采用二维半理论[6]、三维频域理论[7]来预报多体船型的运动性能,得到了相关试验验证。
因此,在船型选型评估中,可以应用引入修正的切片理论、二维半、三维频域理论进行耐波性预报。
3)操纵性预报方法
目前,水面舰船普遍采用MMG分离式水动力模型作为船舶操纵运动数学模型进行操纵性预报。该方法适用于单体船、双体船、三体船操纵性预报,只是针对不同的船型特点,分别计算出方程中的水动力系数。
4 建立综合评估方法
针对水面舰船船型选型的特点,本文提出基于层次分析法和灰色关联度理论船型性能综合评估方法。
4.1 基于层次分析的评估方法
层次分析法 (The Analytic Hierarchy Process,AHP)是20世纪70年代初由美国运筹学家萨提(A.L.Saaty)最早提出的一种多目标评价决策方法。该方法将评价者对复杂系统的评价决策思维过程数学化,即将人的主观判断用数量形式表达和处理。其基本思路是评价者通过将复杂问题分解为若干组成因素,又将这些因素按支配关系分组形成递阶层次结构,通过两两比较、判断及计算,确定各因素的相对重要性。通过这一过程,即可确定各指标的权重,确定方案排序,为选择最优方案提供决策依据。用层次分析法进行综合评估的基本步骤和方法如下:
1)建立递阶层次结构
AHP法第一步是要建立合理的递阶层次结构。一般递阶层次从上至下应包括目标层、指标层、方案层。
2)构造判断矩阵
使评价者对同层并属于同一上层元素的所有元素分别进行两两比较,并通过引入合适的标度,将评判结果用数值表示出来,构造判断矩阵。判断矩阵及权重如表1所示。

表1 判断矩阵及权重表Tab.1 Judgement matix and weight table
表1表示A层因素中ak由下一层中的B1,B2,…,Bn反映。最后一列W是B1,B2,…,Bn对ak的权重。
3)相对重要度计算及一致性检验
①因素相对重要度的计算
首先由下式计算得到判断矩阵的特征向量W。
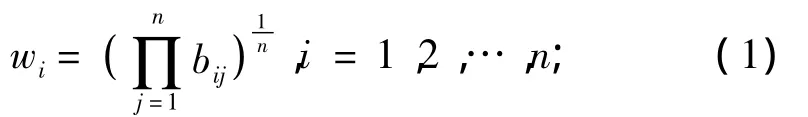
式中n为判断矩阵阶数。再将W进行归一化处理,即


②一致性检验
为保证层次分析得到的结论合理,必须检测判断矩阵的一致性。其步骤如下:
a)计算一致性指标

显然CI的值越接近于0,表明判断矩阵越接近于完全一致性。
b)查找相应的平均随机一致性指标
c)计算一致性比例

当CR<0.1时,认为判断矩阵具有满意的一致性,可以接受;当CR≥0.1时应该对判断矩阵作适当修正。对于一阶、二阶矩阵总是一致的,此时CR=0。
4.2 基于灰色关联度的评估方法
灰色关联度分析方法是灰色系统理论的一支,它是分析系统中各因素间关联程度的一种量化方法,是一种系统分析方法。灰色关联是指事物之间的不确定关联,或系统因子之间、因子对主行为之间的不确定关联。通过灰色关联分析就可以找出各种影响因素与系统发展态势之间的关系,从而分辨出哪些是主要因索、起推动性作用的因索;哪些则是次要因素,对系统的发展没有什么影响。
设A为指标矩阵,E为关联系数矩阵,pj为评估指标,Si为被评估对象,ri为第i个评估对象的评估结果(关联度);R(r1,r2,…,rm)为 m 个评估对象的评估结果 (关联度)矩阵。

式中:aij为第i个评估对象的第j个指标的指标值(i=1,2,…,m;j=1,2,…,n);ξi(j)为第i个评估对象的第j个指标与最优对象中第j个最优指标的关联系数。
1)对原始数据进行标准化处理 (使数据转化为数量级大体相近的无量纲数据)
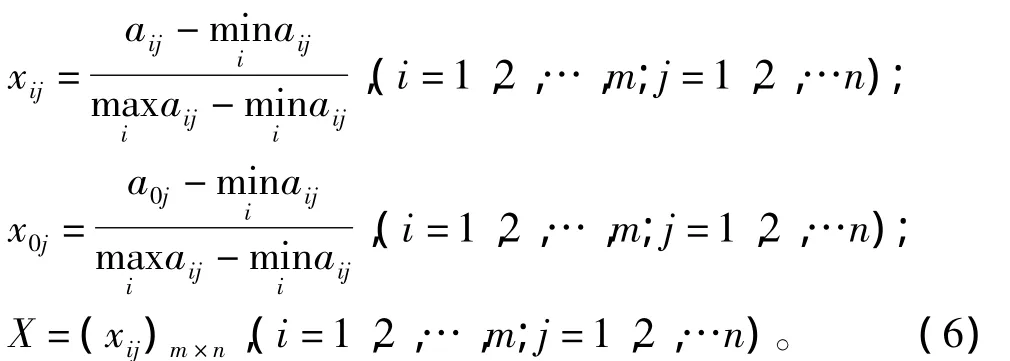
2)确定参考数列和比较数列
设参考数列和比较数列分别为:

式中:x0(k)(k=1,2,…,n)为第 k个指标的最优值;xi(k)为第i个方案的第k个指标的实际值。
3)求关联系数
设第k个指标Xi对X0的关联系数为ξi(k),则各指标的最小绝对误差为

各指标的最大绝对误差为

由此可得关联系数为
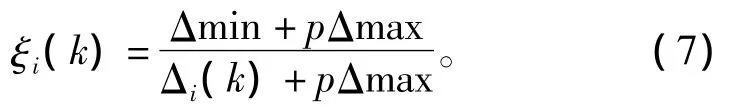
式中:Δi(k)=|xi(k)-x0(k)|;p为分辨系数 (根据经验一般取p=0.5较为合适)。
4)求关联度,根据关联度大小则可知方案的优劣顺序
指标附以不同的权重,则关联度函数为
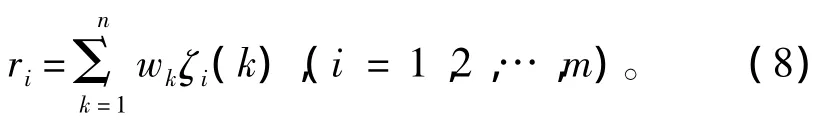
式中wk为指标k的权重。
4.3 基于层次分析与灰色关联度的综合评估模型
结合灰色关联度法与层次分析法,建立综合评估模型,评估过程如下:
1)按建立的综合评估指标体系,采用所确定的理论方法计算各底层指标值;
2)按标准化处理方法将各底层指标标准化;
3)确定比较数列;
4)计算各指标的灰关联系数;
5)按层次分析法采用两两比较法构造判断矩阵,确定各层指标权重;
6)将各方案关联度系数乘以权重后求和得到总的关联度;
7)由总灰关联度大小确定方案排序。评估流程如图4所示。
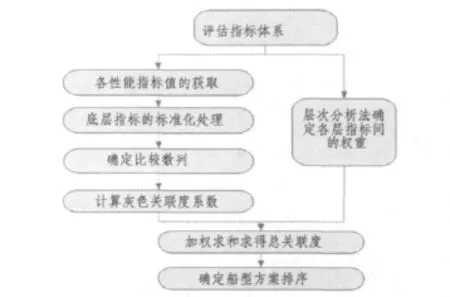
图4 综合评估流程图Fig.4 The process of integrated evaluation
5 算例
5.1 船型参数
本文以某千吨级舰船平台为应用对象,采用所建立的综合评估模型分别对圆舭船型、深V船型、穿浪双体船型、三体船型进行性能综合评估。
1)评估指标体系及指标的计算获取
评估指标体系采用图3所示的指标体系。
采用改进的Noblesse新细长船理论计算阻力性能,采用二维半理论计算耐波性,基于MMG方程预报操纵性,采用静水力原理计算稳性、不沉性指标,计算得到各船型指标如表2所示。
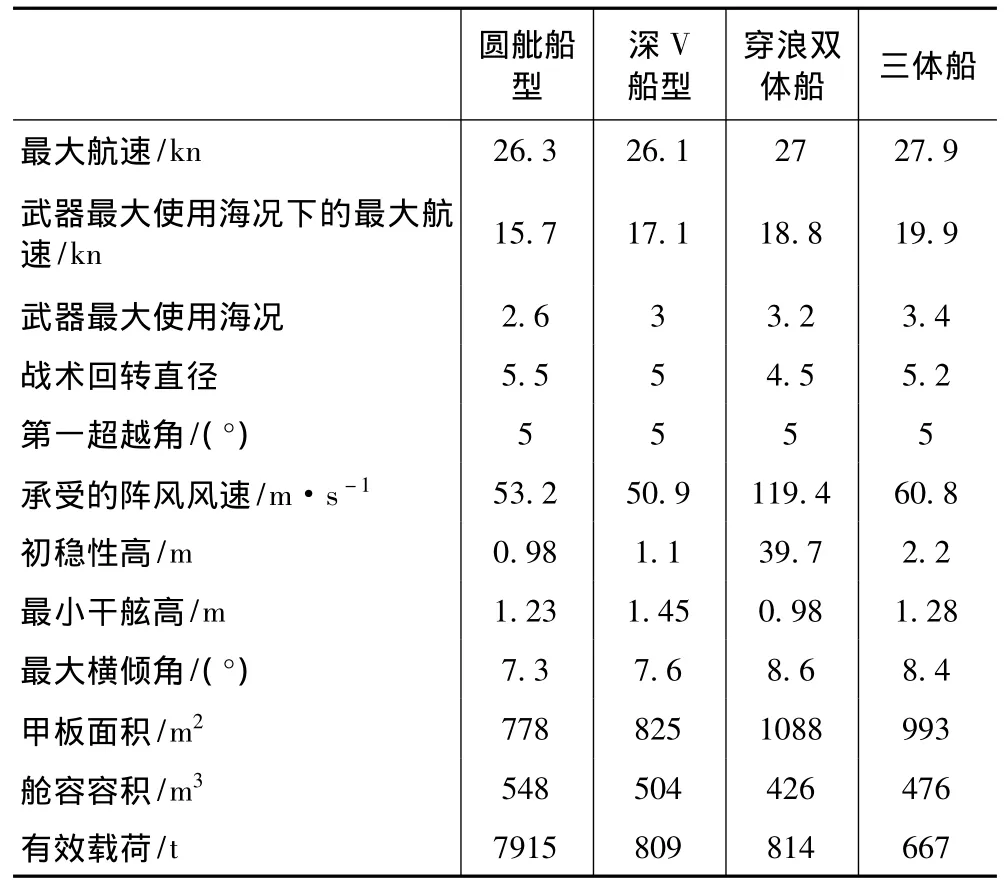
表2 指标计算结果Tab.2 Calculation result
2)底层指标的标准化处理
由式(6)将获取的底层指标进行无量纲化处理,结果如下:

3)确定比较数列
按照各指标的属性,选择最优对象作为比较数列:
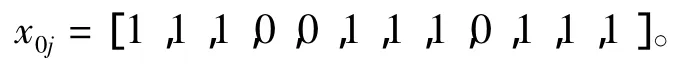
4)计算灰色关联度
由式(7)计算得到关联度系数矩阵:
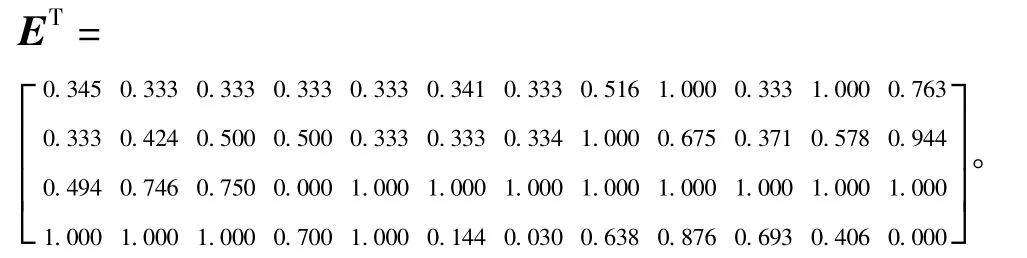
5)确定指标权重
按照层次分析法,通过两两比较确定各层指标的权重,打分采用9分制,采用专家调研法确定比较矩阵。

表3 9点标度法及其含义Tab.3 The 9 interval scale of AHP
如对第一层指标两两比较打分,如表4所示。
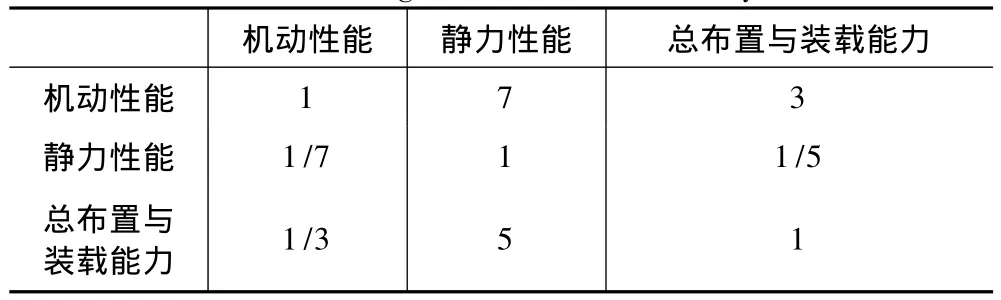
表4 第一层指标权重比较矩阵Tab.4 The weight of the first hierarchy index
由此可得到机动性能权重为0.643,静力性能权重为0.073,总布置与装载能力权重为0.283,其他各层指标可按此方法求得。
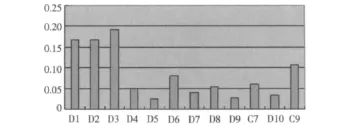
图5 各底层指标总权重Fig.5 The criterion's weights
各底层指标权重为:
a=(0.1671,0.1671,0.1926,0.0488,0.0244,0.0800,0.0400,0.0534,0.0266,0.0594,0.0328,0.1078)
6)加权求和得到总的关联度
按照式(8)加权求和得到综合评估结果为
R= α × E=(0.4314,0.5165,0.6708,0.7294)。

图6 综合评估结果Fig.6 The integrated evaluation result
由综合评估结果可得出几种船型的排序为:三体船型>穿浪双体船型>深V船型>圆舭船型。
6 结语
本文建立基于层次分析与灰色关联度的综合评估模型和评估方法,该方法首先建立指标层次结构,采用理论计算方法获取底层指标值,通过层次分析法确定各指标的权重,然后充分利用已有的白化信息,从被评对象的各个指标值中选取评价标准 (最优值),其实质是评价各被评对象与该标准之间的距离。通过在某千吨级舰船平台上应用表明,该综合评估方法算法简捷,结合了层次分析与灰色关联度分析法的优点,适用于定量化指标的综合评估,该综合评估方法可用于水面舰船船型选型综合评估中,为船型选型决策提供理论依据。
[1]李平.舰船研制指标体系与评估方法研究[D].哈尔滨工程大学,2003.
[2]李云波,黄德波.一种双体船兴波阻力计算方法[J].船舶力学,2002,6(5):9-13.LI Yun-bo,HUANG De-bo.A calculation method for wave resistances oftwin-hullships[J].JournalofShip Mechanics,2002,6(5):9-13.
[3]蔡新功,孙永华.基于Michell理论的多体船阻力计算[J].船舶,2007(2):5-10.CAI Xin-gong,SUN Yong-hua.Calculation about resistance of multi-hull ship based on Michell theory[J].Ship &Boat,2007(2):5-10.
[4]陈京普,朱德祥,何术龙.双体船/三体船兴波阻力数值预报方法研究[J].船舶力学,2006,10(2):23-29.CHEN Jing-pu,ZHU De-xiang,HE Shu-long.Research on numerical prediction method for wavemaking resistance of catamaran/trimaran[J].Journal of Ship Mechanics,2006,10(2):23-29.
[5]缪国平,刘应中,等.切片理论应用于双体船运动计算时的伪共振问题[J].中国造船,1997(2):32-38.MIAO Guo-ping,LIU Ying-zhong,et al.On false resonance in application of strip theory to motion estimation for catamarans[J].Ship Building of China,1997(2):32-38.
[6]段文洋,贺五洲.高速细长体理论在双体船运动计算中的应用[J].工程力学,2002,19(2):140-144.DUAN Wen-yang,HE Wu-zhou.Application of the high-speed slender body theory to motion estimation for catamarans[J].Engineering Mechanics,2002,19(2):140-144.
[7]BINGHAM A E,et al.Motion and loads of a trimaran traveling in regular waves[C].The 6th International Conference on fast Sea Transportation,Southampton,2001.

