基于马尔可夫链模型的铝合金预腐蚀疲劳裂纹扩展表征
李旭东,刘治国,穆志韬
(海军航空工程学院 青岛校区,青岛 266041)
腐蚀损伤可以加速疲劳裂纹的形成与扩展,比单纯的机械疲劳对于金属结构可靠性和完整性威胁更大[1-3]。研究腐蚀环境下疲劳裂纹扩展规律对金属结构的可靠性分析和寿命预测显得尤为重要,对于航空工业意义尤为重大。本文针对6A02航空用锻造铝合金,通过马尔可夫链模型模拟裂纹扩展过程[4-5],建立起腐蚀环境下疲劳寿命的预测表征方法。
1 腐蚀疲劳裂纹扩展试验
1.1 实验材料
试验件材料为6A02铝合金,其化学成分为(wt.%):Al,92.5%;Cu,4.5%;Mg,1.42%;Mn,0.74%;Fe,0.26%;Si,0.19%;Zn,0.13%。抗拉强度450MPa,屈服强度342MPa。为了便于捕捉到裂纹,试验件为含单边缺口SENT狗骨状试件,其形状如图1所示。
1.2 实验方案
由于飞机在飞行过程中主要承受机械疲劳,而在地面停放的时候主要承受来自于环境的腐蚀损伤,因此在其任务剖面中存在“疲劳-腐蚀-再疲劳-再腐蚀”循环,因此本文采用对试件进行预先腐蚀,然后对腐蚀试件再进行疲劳加载的实验方案。
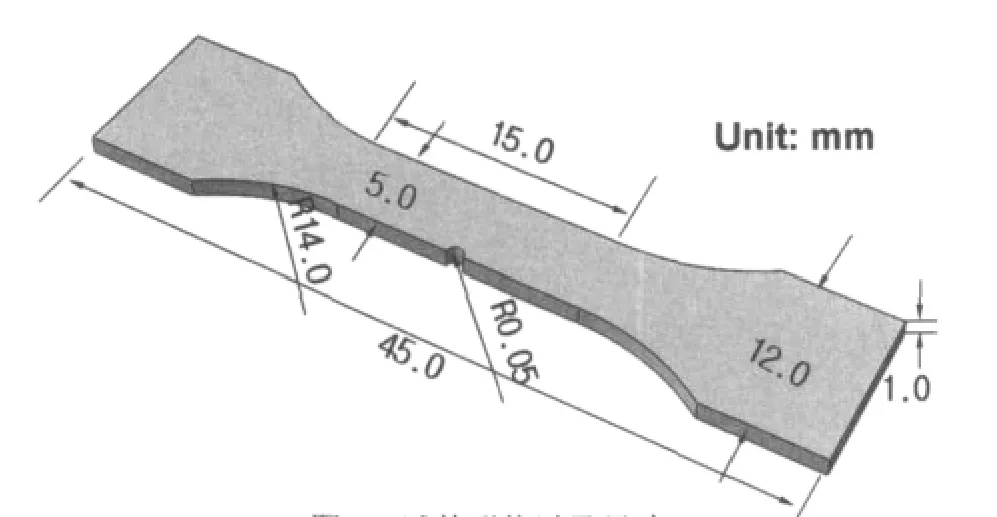
图1 试件形状以及尺寸
对于铝合金而言,EXCO溶液腐蚀是一种常用的腐蚀方式,其实验数据重复性好[4]。基于ASTM G34标准,配置标准EXCO溶液,然后将铝合金试件在腐蚀溶液中浸泡10小时,以模拟环境带来的腐蚀损伤。
疲劳实验采用带疲劳加载装置的SS550(Shimadzu,Japan)扫描电镜完成。试验在室温条件下进行,对试验件进行轴向拉-拉疲劳加载,波形为正弦波,最大加载应力为250MPa,应力比为0.1,加载频率为5Hz。在疲劳加载过程中,通过扫描电镜图像记录系统进行疲劳试件表面原位拍照,每间隔1000个应力循环次数记录1次裂纹长度及相应的循环数,直到试验件断裂为止,如图2所示。

图2 试件不同循环次数下的SEM图片
2 结果与分析
2.1 实验数据分散性
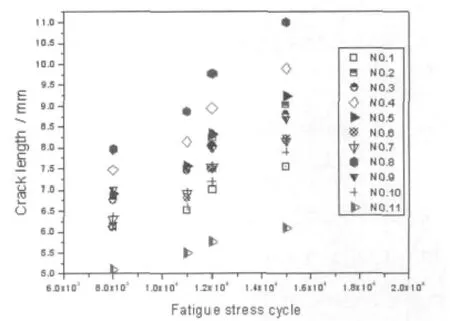
图3 不同循环数的裂纹长度分布
从图3所示的部分实验结果可以很明显的发现疲劳裂纹扩展试验数据存在较大的分散性。即使是宏观上不存在任何差别的试样在严格控制的试验环境下,得到的疲劳裂纹扩展试验结果也会相差很大,裂纹扩展存在分散性的同时,也具有统计特性,疲劳裂纹扩展具有较大的统计变异性[3-4]。因此,在进行飞机结构疲劳裂纹扩展分析时,可采用统计分析的方法,通过马尔可夫链模型模拟疲劳裂纹的扩展[5]。
2.2 基于马尔可夫链模型的腐蚀疲劳裂纹扩展表征
2.2.1 马尔科夫过程
马尔可夫过程是随机过程的一种。它是研究系统“状态”与“状态”之间的关系。假如系统完全由定义为“状态”的变量的取值来描述,则该系统处于一个“状态”。假如描述系统的变量从一个状态的特定值变化到另一个状态的特定值时,则该系统实现了状态的转移。并且这样的状态转移的过程完全是随机的,它们的转移规律不能以确定的规律进行,而只能按某种概率转移。一般地,系统在时刻所处的状态为已知的条件下,过程在时刻所处状态的条件分布与系统在时刻之前所处的状态无关的特性称为马尔可夫性或无后效性。即:系统“将来”的情况与“过去”的情况是无关的。时间和状态都是离散的马尔可夫过程称为马尔可夫链模型,它是一种累积损伤概率模型,可以描述各种随机损伤的寿命分布和损伤状态分布。
2.2.2 腐蚀疲劳裂纹扩展的马尔科夫链模型
在腐蚀疲劳裂纹的扩展研究中,重点关注的是裂纹长度X随着应力循环次数t变化(0 ≤t≤Nf,Nf为结构的疲劳寿命)。为此可以将应力循环次数划分为若干状态0≤t1<t2<t3< .....≤Nf,相应的与每个状态对应的都会有裂纹长度 0 ≤X1<X2<X3<.....≤Xfracture(Xfracture为试件断裂时的裂纹长度),这样就构成了一个随机变量序列{X(t),t∈Nf}。
做如下假设,{X(t),t∈Nf}满足:
1)时间集合为非负整数集Nf={n=0,1,2,},对应于每个时刻(应力循环次数),状态空间为离散集,即E= {n= 0 ,1,2.....},即X(t)为时间离散状态离散变量。
2)对任意的正整数s, m, k,及任意的非负整数js> . ....>j2>j1,与相对应的状态im+k,im,ijs,...,ij2,ij1,
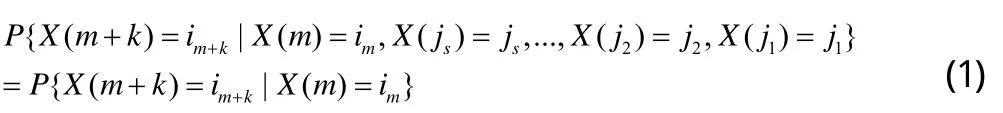
恒成立。
则{X(t),t∈Nf}为马尔科夫链。当k=1时,式(1)变为
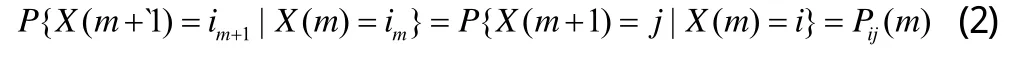
它表示裂纹长度在m时刻长度为i,在m+1时刻长度为j的一步状态转移概率。
根据马尔科夫链模型的假设,在一个迭代步之后的裂纹扩展情况只取决于在这个迭代步的损伤程度和这个迭代步本身,与这个任务循环之前损伤的累积过程无关,任一时刻的损伤状态完全由初始损伤状态和概率转移矩阵来决定。
一般来说,状态转移概率是与迭代步m有关,是迭代步的函数。若状态转移矩阵与迭代步无关,为恒定值,则为齐次状态转移概率。本文假设{X(t),t∈Nf}符合齐次马尔科夫链模型,设状态转移矩阵P为常量矩阵。若当前时刻的裂纹概率分布为p(n),前一个应力循环的裂纹长度概率分布为p(n- 1 ),则p(n)=p(n- 1 )P。根据递推关系得到经过K个迭代步以后裂纹长度的概率分布为p(K)=p( 0)PK。若设初始状态裂纹长度概率分布为

则:

令Dk表示第k个应力循环之后裂纹长度的概率分布,则pk(j)=P{Dk=j),表示第k个离散化的应力循环之后裂纹长度为j的概率。根据马尔科夫模型可以求得给定应力循环时裂纹长度的概率分布为

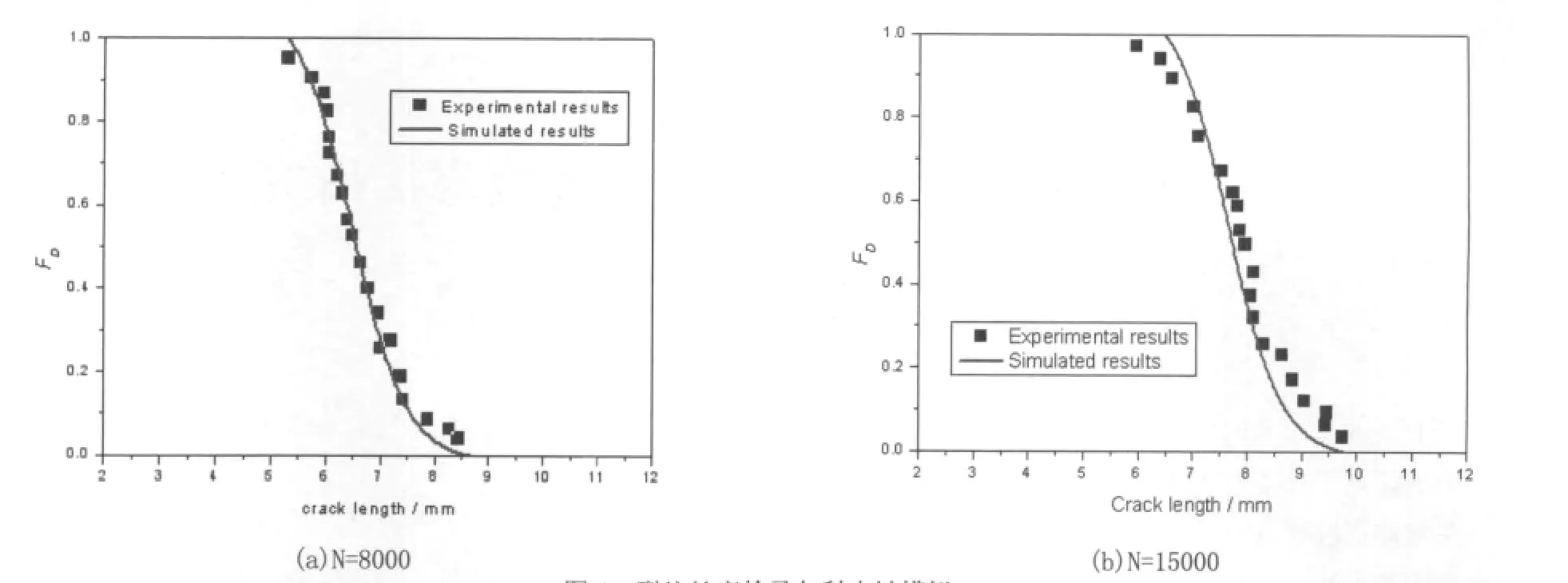
图4 裂纹长度的马尔科夫链模拟
基于如上所述的马尔科夫链,对于1.2节所述的裂纹扩展实验数据进行仿真,每隔1000个应力循环设为一个迭代步,得到6000次循环和13000次循环后的裂纹长度概率FD分布曲线如图4所示,与实验得到的累计概率分布误差较小,说明基于马尔可夫链模型的腐蚀疲劳裂纹扩展具有较高的预测能力,对腐蚀环境下飞机铝合金结构的寿命预测和可靠性分析具有参考价值。
分析式(4)所示的腐蚀疲劳裂纹扩展马尔可夫链模型,它的每一步裂纹长度分布预测都是基于初始步裂纹分布信息p( 0)= (a1,a2,....,am)进行预测的,而且假设转移矩阵不变,随着预测步的增多,真实值与预测值的差别会越来越大,预测的准确性也会逐步降低。图4(b)所示的15000个应力循环后裂纹长度预测分布与实验分布误差相对图4 (a)8000个应力循环的误差明显增大。根据齐次马尔科夫链模型的平稳分布特征,经过足够多的步数之后,该模型会导致预测结果趋向于一个固定的裂纹分布状态,显然与实验现象不相符合。这样就大大影响了基于马尔科夫链过程的裂纹扩展模型的长期预测准确性。因此如何对腐蚀疲劳裂纹马尔可夫链模型进行改进,使得模型能够更新当前迭代步的信息,并自动更新状态转移矩阵P,将是提高基于马尔可夫过程的腐蚀疲劳裂纹扩展预测方法工程实用性的重要努力方向。
3 结论
1)腐蚀疲劳裂纹扩展具有非常强的不确定性,必须利用统计学方法进行表征。
2)腐蚀疲劳裂纹扩展过程可以用离散化的马尔科夫链模型进行评价。
3)本文提供的基于马尔科夫链的腐蚀疲劳裂纹预测方法准确性会随着预测步数的增加而下降,需要进一步进行改进。
[1] Chen G S, Liao C M. Pitting corrosion and fatigue crack nucleation, effects of the environment on the initiation of crack growth[S]. ASTM STP 1298, American Society for Testing and Materials, 1997.
[2] Duquesnay D L, Underhill P R, Britt H J. Fatigue crack growth from corrosion d amage in 7075- T6511 aluminum alloy under aircraft loading [J]. International Journal of Fatigue, 2003 (25): 371-377.
[3] Liou H Y, Ni C C, Wu W F. Scatter and statistical analysis of fatigue crack growth data [J]. Journal of Chinese Society of Mechanical Engineers, 2001, 22(5): 399-407.
[4] Bogdanoff J L, Kozin F. Probabilistic models of cumulative damage [M]. New York: Wiley, 1985.
[5] Wu W F, Ni C C. A study of stochastic fatigue crack growth modeling through experimental data [J]. Probabilistic Engineering Mechanics, 2003(18): 107-118.

