产生m子序列的一种实用算法
方俊初,吕 虹,张爱雪
(1.安徽工程大学电气工程学院,安徽芜湖241000 2.安徽建筑工业学院电子与信息学院,安徽 合肥230022)
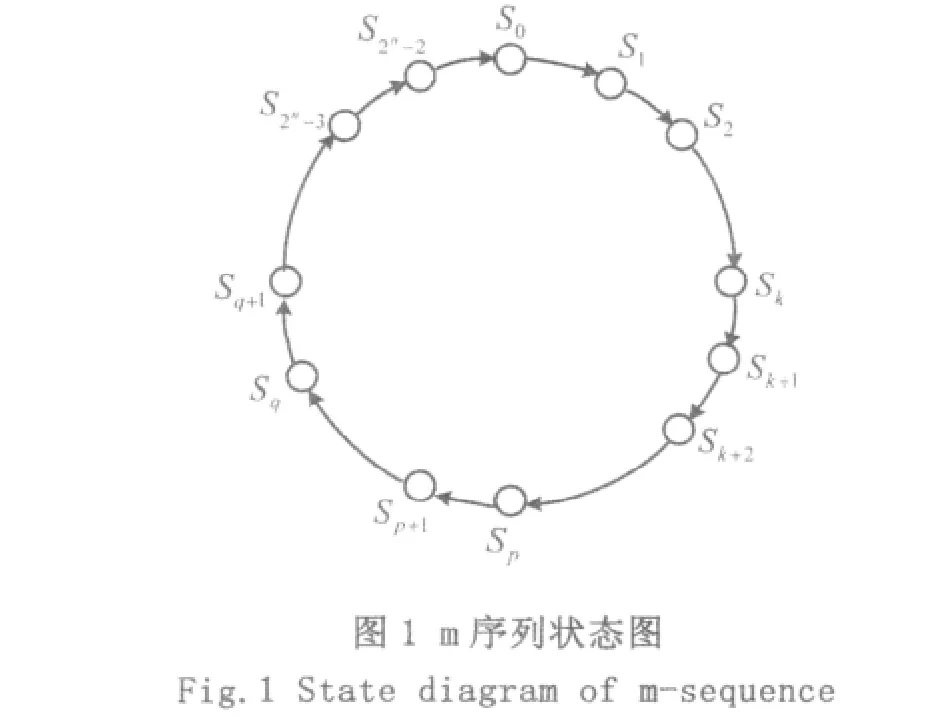
若n级移位寄存器的特征多项式为n阶本原多项式,则该移位寄存器从任意一个非“0”状态出发所形成的状态图是一个包含2n-1个状态的大“圈”,如图1所示。由它产生的GF(2)序列的周期也是2n-1,称为最大长度序列,即m序列,是一类常用的伪随机序列。在这2n-1个状态中,某状态S的下一个状态称为S的“后继”,而S的前一个状态称为 S的“前驱”。而形如 S=(α0,α1,α2,…αn-1),S*=(α0,α1,α2,…)则称为一对共轭状态。
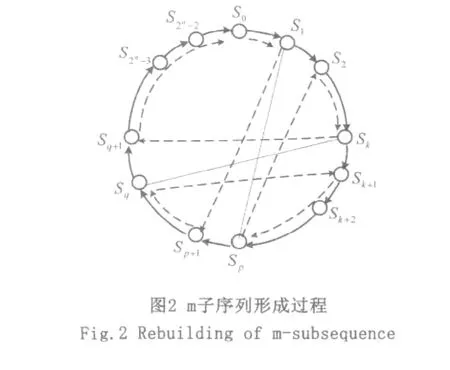
若两对共轭状态的连线在“圈”内存在交点,则交换它们的后继仍能形成一个长度为2n-1的大“圈”,与这个新的状态转换较图对应的序列称为原序列的子序列[1-2]。子序列形成过程如图2所示,图中S1和Sp是一对共轭状态,Sk和Sq是另一对共轭状态。实线箭头表示原有的状态转换方向,虚线箭头表示新的状态转换方向。
在图2所示过程中,两对共轭状态的连线(图中实线所示)在圈内相交是这一转换过程成功的关键。但是单从状态转换的角度来判断哪两对共轭状态在“圈”内有交点存在很大的困难,因而文献[1] 只在每一级中确定了一个子序列的生成方法。
实际上,在n阶本原多项式f(x)决定的线性移位寄存器中共有2n-1个状态,因为00…01在圈内没有共轭状态,其余状态将两两互为共轭,因此共有对共轭状态,这些共轭状态中符合上述交换条件的可能有很多,如何能快速准确的找到这些满足条件的共轭状态呢?又如何通过它们简便而又快速地实现这些m子序列呢?本文利用数学变换思想,建立了一种“映射”,将GF(2)域中“状态”映射到整数域中,共轭状态可以用编码表示,通过该编码很容易判断出两对共轭状态在圈内有没有交点。
1 建立一种映射关系
表1是以GF(2)上以本原多项式f(x)=1+x2+x5为反馈函数生成的移位寄存器的状态表[3-4]。
定义1:在给定本原多项式的基础上,从任意一个初始状态S0出发,按照状态出现的先后顺序将这些状态依次记为 S0、S1、S2… S2n-2下标 0、1、2…(2n-2)是该状态的序号。
某个状态的前驱与后继仅与反馈函数相关而与初始状态无关。因而可以得出:两对共轭状态在圈内的连线是否会相交,与初始状态的选择无关[5]。
这样2n-1个“状态”就和0、1、2…2n-2共(2n-1)个整数建立了“映射”关系。编程时,假设这些状态以数组的形式存在,那么知道了这个“序号”就可以找到(“引用”)该“状态”,已知“状态”也可以判断其在“圈”中的位置。这为下面研究共轭状态的相互关系提供了方便。
2 共轭状态的表示方法
定义2:某一状态为 Sk=(α0,α1,α2,…αn-1),设其共轭状态为Sp=,将它们的连线画在圈内,若k<p则将这一对共轭状态记为[k,p] ,若 k>p则将这一对共轭状态记为[p,k] ,称为这一对共轭状态的“坐标”。
共轭状态的“坐标”包含了这一对共轭状态在圈中的位置信息。[k,p] 中k称为起点,p为终点,按上述定义,起点值一定比终点值要小,即要求0≤k<p≤2n-2,举个例子说,表1中S3和S5是一对共轭状态,将其坐标记为[3,5] ,而不是[5,3] 。这样规定有两个目的,一是确定了每一对共轭状态只有唯一的一个坐标了;二是方便用“遍历”法生成共轭状态表。有了共轭状态表,就可以通过这些坐标来研究共轭状态在圈中的相互关系了。表2是根据表1按上述定义2编程得到的共轭状态表。由表2可见共轭状态表的特点一是起点是按从小到的顺序排列的,二是每一对共轭状态在表中只出现一次。
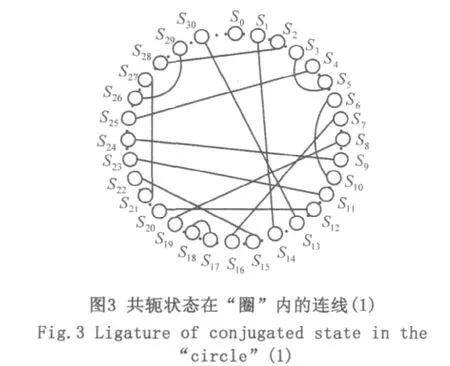
图3画出了表2中共轭状态在圈中的连线。可见,这些共轭状态的连线在圈内的有的存在交点,有的不存在交点。有交点就可以产生新的序列,问题是在没有画出这个“圈”的情况下,如何才能确定两对共轭状态在圈内有无交点呢?

表1 状态表实例Tab.1 An example of state table

表2 共轭状态表Tab.2 Conjugated state table
3 子序列生成条件的简便判断
观察图3中这些连线的相互关系,并结合表2,可以得到下面的定理。
定理1:若[k,p] 是一对共轭状态,[m,n] 是另一对共轭状态,将起点坐标较小的这一对共轭状态称第一对共轭状态,另一对称为第二对共轭状态,这里假设[k,p] 是第一对共轭状态,若k<m<p<n,则这两对共轭状态的连线在圈内一定有交点。
证明:第一对共轭状态[k,p] 的连线将“圈”一分为二,从起点出发,顺时针方向的一侧称为“右侧”,逆时针方向的一侧称为“左侧”。k<m<p即第二对共轭状态的起点位于第一对共轭状态的“右侧”,而 n>p,根据定义1,则容易知道 n> k,即第二对共轭状态的终点一定位于第一对共轭状态的“左侧”,因而这两对共轭状态的连线在“圈”内必有交点,证毕。
定理1用数学语言将原来只能用文字表述的交换条件“数学化”了,这种数字化的结果是很方便编程统计出交点的个数,也能方便地判断两对共轭状态是否满足交换条件。例如上图中的共轭状态[1,14] 和[2,28] 在圈内有交点,而[1,14] 和[6,10] 在圈内就没有交点。
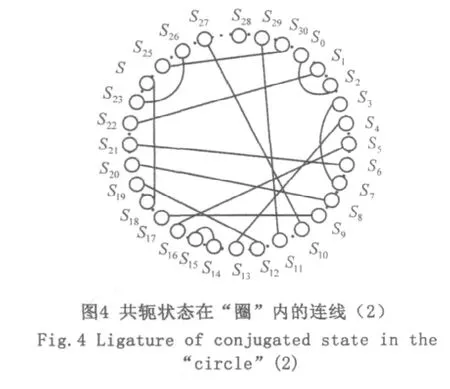
应当指出的是,在反馈函数确定的情况下,初始状态不同,则各状态在圈中的序号都将改变,共轭状态的坐标也就改变,如图4所示。用上述定义1规定的共轭状态的表示方法仍能反映各共轭状态在圈中的相互关系,如图3中[1,14] 和[2,28] 对应在图4 就是[11,29] 和[25,30] ,仍可判断它们的连线在圈内有交点。而图3中的[1,14] 和[6,10] 在图 4 对应的坐标是[11,29] 和[3,7] 仍能判断它们在圈内没有交点。
总之,共轭状态在圈内是否有交点与初始状态无关,从任一个初始状态出发进行编号,并按定义1生成的共轭状态表都能准确反映共轭状态在“圈”内的相互关系。
4 应用
4.1 子序列个数的统计
从一个已知的m序列的状态图,可以得到多少个子序列呢?显然,这取决于共轭状态的连线在圈内有多少个交点,有了共轭状态表,只需按定理1统计出交点的个数,就是能生成的子序列的个数了。

实验结果:经过实验发现,相同级数的本原多项式对应的线性移位寄存器的共轭状态在圈内的交点数是相同的,例如前面讲的以f(x)=1+x2+x5为反馈函数的移位寄存器,其共轭状态在圈内的交点数为35,若反馈函数换为f(x)=1+x3+x5,其共轭状态在圈内的交点数也是35,其他的五阶本原多项式的情况也是如此。表3给出的是通过实验得到的级数为5-10级的线性移位寄存器共轭状态在圈内的交点数(子序列个数)。
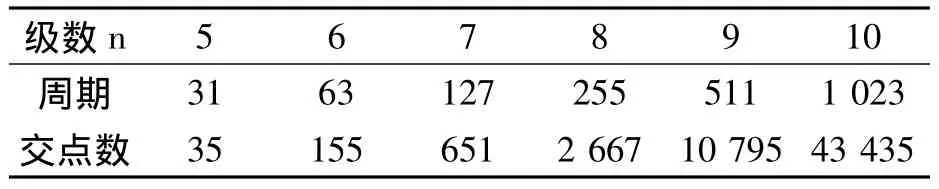
表3 共轭状态交点数Tab.3 The number of intersect points
我们知道,n阶线性移位寄存器所能产生的m序列(由不同的本原多项式产生)的数目远小于m序列的周期N,但从表3可以看出,一个本原多项式衍生出的子序列的数目则远远大于它的周期,这些子序列保留了m序列的优秀伪随机特征。
4.2 子序列的生成
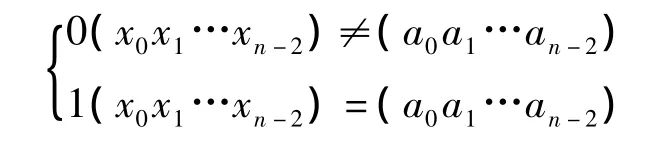
下面以定理的形式给出生成m子序列的一般方法。
定理2:若[k,p] 是一对共轭状态,[m,n] 是另一对共轭状态,若k<m<p<n,或m<k< n < p,则在移位寄存器的反馈函数中加上(模2加)第m项和第k项的特征小项后,该移位寄存器的状态图将形成一个新的长度为2n-1的大圈。对应此大圈将产生一个新的不同于原来的序列。
证明:k<m<p<n,或m<k< n < p保证了两对共轭状态在“圈”必有交点。移位寄存器的反馈函数中加上(模2加)第m项和第k项的特征小项,意味着在上述四个状态后面的反馈函数值取反,即交换了次状态,重新形成了新的大“圈”,证毕。
简单地讲,交换共轭状态的后续状态就是在状态生成过程中,遇到共轭状态中的一个就将原反馈函数值取反[7-8]。
程序实现的思路是:指定反馈移位寄存器的级数,输入相应的本原多项式的系数,从任一初始状态出发,将全部状态生成并按顺序储存,根据共轭状态的特点自动生成共轭状态表,给定一对共轭状态,判断是否符合交换条件,若符合交换条件,再次生成状态表时在该状态的下一个状态输出前通过异或“1”改变原有的反馈函数值。这中间可以用序号引用该状态[9-10]。
本文根据上述思想设计了程序,只要改变几个常数就可以生成任意级数本原多项式的全部m子序列或其中一个子序列,运行非常方便,非常适用在需要大量伪随机序列的场合。
5 结论
1)本文解决了“如何判断两对共轭状态在圈内有交点”这一形成子序列的关键问题。解决问题的思路简洁,非常便于程序实现。
2)本文介绍的方法可以在本原多项式的基础上可方便地产生大量的m子序列,为进一步研究这些子序列的性能奠定了基础,也必将进一步扩展伪随机序列在测量、通信、流密码等领域中的广泛应用。
[1] 吕 虹,段颖妮,管必聪,等.第一类m子序列的构造[J] .电子学报,2007(10):2029-2032.
[2] LV HONG.Design and implementation of a maximal length nonlinear pseudorandom sequence[C] .Proceedings of the 2009 International Conference on Computer and Communications Security.2009:12 -16.
[3] 谢深泉.De Bruijn序列间的映射及升级算法[J] .计算机工程与应用,2007(22):12-15.
[4] 谢深泉.De Bruijn序列查寻表标签的定值构造法[J] .计算机工程与应用,2008(19):37-40.
[5] LAN JINGJING,GOH WANG LING,KONG ZHI HUI,et al.A random number generator for low power cryptographic application[C] .Proceedings of the 2010 International Soc.Design Conference,ISOCC 2010,328-331
[6] 林智慧,陈绥阳,王元一.m序列及其在通信中的应用[J] .现代电子技术,2009(09):49-52.
[7] 苏绍璟,伍文君,黄芝平,等.含错m序列本原多项式的高阶统计测定算法[J] .兵工学报,2010(12):1593-1597.
[8] 张晓林,佟婧,李佑虎.高阶统计分析的m序列检测新方法[J] .哈尔滨工程大学学报,2010(03):386-390.
[9] 贾银洁,赵丽娟,许鹏飞.扩频系统中伪随机码发生器的实现[J] .现代计算机(专业版),2008(05):72-74.
[10] 熊睿佳,胡万利.伪随机m序列特性及C语言实现[J] .工程地球物理学报,2011(01):110-112.

