基于改进ACO与PSO算法的结构可靠度分析

李彦苍，恒北北，彭双红，程秋月，伴晨光

(河北工程大学土木工程学院，河北邯郸056038)

可靠度在结构设计中的应用始于20世纪40年代，其核心内容是结构可靠指标的计算。工程中常用的可靠指标计算方法主要有一次二阶矩法、JC法、梯度优化法以及响应面法、蒙特卡罗法及随机有限元等［1－7]。使用这些方法常会遇到很多复杂问题难以解决，如极限状态曲面难以解析描述，仿真计算量大，难以做到有效搜索解空间来找到标准正态空间原点至极限状态曲面的最短距离［8]以及最弱失效路径［9]等问题。近几年来，计算群体智能算法［10]迅猛发展，其中粒子群算法(Particle Swarm Optimization PSO)和蚁群算法(Ant Colony Optimization ACO)可用在系统设计、多目标优化、模式识别、信号处理、决策制定、工件排序、车辆调度、建设工程等领域［11－17]，并表现出在求解组合优化问题上所具有的独特优势。

本文通过引入信息熵，优化参数τ，对ACO算法进行改进，进而确定结构失效路径;再使用PSO算法对结构进行可靠指标的求解。并以十杆桁架为例，分别采用响应面法、改进遗传算法与本算法对其可靠度指标进行对比分析。

1 基于改进后的ACO的失效路径的寻找

1.1 ACO 简介

ACO由一系列模拟现实中蚁群觅食过程的算法组成。以TSP问题为例，设m是蚁群中蚂蚁的个数，n为城市数，τij表示t时刻在 i j连线上的信息量，ηij为蚂蚁由城市i转移到城市j的期望信息。初始时刻，各条路径上的信息量相等。Pkij(t)表示在t时刻蚂蚁由位置i转移到位置j的概率，则

信息素的更新公式为

1.2 ACO 改进

为了解决基本蚁群算法的过早收敛问题，采用文献［18] 方法，即通过引入信息熵H，控制信息熵的值，来改进参数τ，进而对蚁群算法进行改进。开始时每条路径都会有等量的信息素，信息熵取最大值，随着信息素的增加，信息熵值逐渐变小，继续进行容易出现早熟以使算法出现停滞现象，所以此时通过控制与信息熵有关的α(t)和β'(t)的值来控制此时最优路径出现的区域和信息素更新的范围，进而避免了早熟和停滞现象的发生，找到最优路径。

1.3 改进后的ACO寻找最短失效路径

所谓失效路径就是由初始结构所处的状态到结构失效状态之间的任一条路径。对于一个结构来说会有多条失效路径，每条失效路径又包括多个结构单元。其中最弱失效路径就是结构单元依次按可靠指标最小失效，直至整个结构体系失效的一条路径［9]。

对于ACO求解 TSP问题［19]，启发式信息 ηij(d为城市i到城市j的距离)，所以当通过改ij进后的蚁群算法寻找结构失效路径时，可以假设启发式信息(β为结构单元的可靠指标)，蚂蚁数为m，结构单元数为n

使用ACO寻找失效路径的操作步骤如下:

1.初始化参数，τij(0)=0。

2.将m只蚂蚁放在n个结构单元上。

3.按公式(1)计算每只蚂蚁移动到下一个结构单元的概率，根据概率选择蚂蚁的移动方向。

4.m只蚂蚁遍历n个结构单元后，路径上的信息素增加。

5.所有路径信息素按公式(2)(3)更新，进行局部寻优。

6.多次重复(3)－(5)步，进行全局寻优，找出最优路径。

2 基于PSO的可靠指标计算模型

2.1 PSO 简介

PSO将每个个体看成搜索空间中的一个没有体积的粒子，在空间中以一定的速度飞行。对于第i个粒子，它经历的最好位置为Pbest，记为Pi，在群体中所有粒子经历过的最好位置为gbest，记为Pg。粒子根据如下公式来更新自己的位置和速度

式中，ω－惯性权重;c1和c2－加速度常数;rand1和rand2－两个在［0，1] 范围内的随机函数;－第k次迭代粒子i的飞行速度－第k次迭代粒子i的位置。

2.2 模型建立

在结构可靠度分析中，结构可靠指标β的几何意义是标准正态空间内，坐标原点到极限状态曲面的最短距离。

x1，x2，…，xn是结构中的随机变量，由这些随机变量组成的极限状态方为z=g(x1，x2，…，xn)=0。

把β看成极限状态曲面上点P(x1，x2，…，xn)的函数，通过优化求解，找到β最小值。

约束优化模型:

式中，μxi，σxi－随机变量 xi的均值、标准差。

采用罚函数法将式(6)变成相应的无约束优化问题:

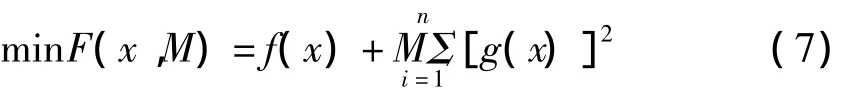
式中，M－相应的罚因子(足够大的正数)，相应的项为罚项。

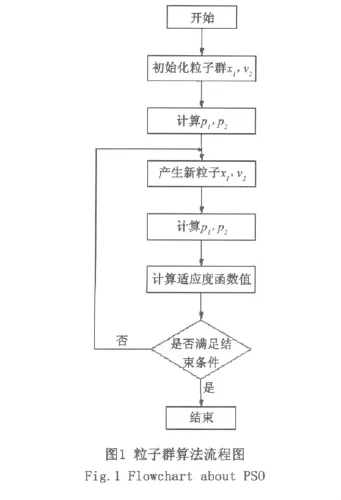
粒子群算法的流程如图1所示。

3 实例分析

10杆桁架结构如图2所示，各杆的横截面积为正态分布的基本变量，均值为6.452×10－3m2，变异系数为 0.05，杨氏模量为 6.895 ×1010pa，施加的荷载为p1=p2=4.45×105N，结构极限状态函数取为桁架的最大位移不超过最大允许位移为0.101 6m，求此时的可靠度。

首先采用改进的ACO确定结构的失效路径，进而通过PSO算法对可靠指标进行求解。在求解过程中，每代产生20个粒子数。粒子群算法的迭代收敛过程如图3所示。图中表示最优粒子的迭代收敛过程图，可以看出在第十次迭代过程中最优粒子已经收敛达到最好的精度，随着进一步迭代全部粒子收敛到最优值。此算法经过十次迭代，得到的可靠指标为0.682 37，相应的设计点坐标为(6.311 0，6.436 6，6.315 0，6.443 6，6.452 6，6.443 6，6.384 5，6.389 0，6.428 4，6.409 5)，从文献［21] 中可以得到响应面法与遗传算法在计算本结构时的可靠指标及相应的设计点坐标。三种算法计算结果比较见表1。

与响应面法［20]的迭代过程相比，PSO采用较少的粒子数，就能达到较好的计算精度。与遗传算法［21]相比，PSO算法由于具有强大的全局寻优能力，迭代收敛速度快，对于处理复杂的极限状态方程问题，具有良好的适用性。

表1 三种算法计算结果比较Tab1.Three algorithms comparison of results

4 结论

1)引入信息熵，对参数 进行调整，避免了ACO的早熟和停滞现象发生，快速的找到最优路径。

2)在ACO找到最优路径的情况下，PSO能够通过较少的粒子数，快速收敛，求出更准确的目标函数值。

［1] MOSES F.System reliability developments in structural engineering［J] .Structural Safety，1982，1(1):3 －13.

［2] 张 明.结构可靠度分析－方法与程序［M] .北京:科学出版社，2009.

［3] 谭海涛，徐定海，王善.一种计算结构可靠度的一元分解法［J] .哈尔滨工程大学学报，2009，30(8):883－886.

［4] 张建仁，许福友.计算结构可靠指标的子域抽样法［J] .土木工程学报，2003，36(12):39－43.

［5] 周彬彬，顾祥林，张伟平，等.海洋大气环境下钢筋混凝土梁受弯时变可靠度分析［J] .土木工程学报，2010:15－21.

［6] 吕大刚，贾明明，李刚.结构可靠度分析的均匀设计响应面法［J] .工程力学，2011，28(7):109－116..

［7] 武清玺.结构可靠性分析及随机有限元法［M] .北京:机械工业出版社，2005.

［8] 阎宏生，胡云昌，李向京.结构可靠性分析的一种新方法［J] .天津大学学报，2000，33(6):32－35.

［9] 蔡文学，程耿东.灾害荷载下弹塑性结构体系可靠度的近似计算［J] .大连理工大学学报，1996，36(1):6－12.

［10] 梁艳春，吴春国，时小虎，等.群智能优化算法理论与应用［M] .北京:科学出版社，2009.

［11] LIU Q，WANG C G.A discrete particles swarm optimization algorithm for rectilinear branch pipe routing［J] .Assembly Automation，2011，31(4):363－368.

［12] 周书敬，潘靖.基于改进蚁群算法的钢管混凝土构件的优化［J] .河北工程大学学报:自然科学版，2011，28(4):10－13.

［13] MOUSA F M.Particle swarm optimization algorithm for smart antenna system［J] .Journal of Mobile Communication，2011，5(1):6－10.

［14] 赵文红，张红斌.一种改进的粒子群优化算法［J] .河北科技大学学报，2006，27(4):317－320.

［15] 李正涛，赵环宇，马献果.应用粒子群算法从已知数据中确定置信测度和似然测度［J] .河北科技大学学报，2011，32(2):128－132.

［16] 周书敬，薄 涛，史三元.混合算法在轻钢结构优化设计中的应用［J] .河北工程大学学报:自然科学版，2011，28(2):71－74.

［17] 张浩，彭晓华，孟宇.基于连续域蚁群改进算法的T－S模型辨识［J] .黑龙江科技学院学报，2007，17(1):74－78.

［18] LI Y C，LI W Q.Adaptive ant colony optimization algorithm based on information entropy:foundation and application［J] .Fundam Inform，2007，77(3):229－242.

［19] YANG J H，SHI X H，MARCHESE M，et al.An ant colony optimization method for generalized TSP problem［J] .Progress in Natural Science，2008，18(11):1417－1422.

［20] 张银龙，常大民.响应面法用于桁架体系可靠度分析［J] .工程设计CAD与智能建筑，2002(11):57－60.

［21] 魏锦辉，董笑慧，魏保立.遗传算法及其在结构可靠度计算中的应用［J] .河南科学，2009，27(10):1261－1263.