基于AHP的高校公共选修课管理优化研究
徐海玲
(江苏科技大学 教务处,江苏 镇江 212003)
基于AHP的高校公共选修课管理优化研究
徐海玲
(江苏科技大学 教务处,江苏 镇江 212003)
随着学分制在高校的施行,选课制也随之发展起来.高校为拓宽学生视野、扩大学生知识面提高学生综合素质开设校公共选修课.然而很多高校由于多校区办学、师资尤其是专业方向教师不足等等原因形成公共选修课选课爆满现象.本文使用层次分析法对选课主体进行抽签,来优化校公共选修课的管理.
公共选修课;高校;AHP
1 引言
随着高等教育大众化进程的推进,高校纷纷于20世纪90年代实行学分制并开设公共选修课来拓宽学生视野、扩大学生知识面、提高学生的综合素质,以此适应社会经济发展的需求.然而由于资源的限制在校公共选修课的管理上存在很大的难度.首先,由于高等教育的发展,国家为解决高等院校规模小、学科单一等问题对高校的布局和管理体制进行了调整和改革.国内很多高校进行联合与合并或扩展新校区,这就加大了高校在教务管理上的难度.其次,由于高校规模的扩大和高校招生扩招,这使得高校教师资源不足,尤其是专业教师.这也影响了校公共选修课开课量.最后,选课制的特点就是容许学生选择自己感兴趣的课程.这就形成了校公共选修课的一些课程选课爆满现象.本文针对部分选修课爆满这一现象,使用层次分析法对选课主体进行排序抽签,来优化校公共选修课的管理.
2 层次分析法原理
AHP(Analytic Hierarchy Process)层次分析法是美国运筹学家Saaty教授在20世纪80年代提出的一种多方案或多目标的决策方法.层次分析法首先将所要分析的问题层次化,根据问题的性质和要达到的目标,将问题分解成不同的组成因素,按照因素间的隶属关系,将因素按不同层次聚集组合,形成一个多层次分析结构模型,最终归结为低层方案相对于高层目标的相对重要程度的权值或相对优劣次序的问题[1].然而层次分析法在设置两两判断矩阵主要依靠的是人的主观经验,这就造成了判断矩阵不太合理.本文在构造两两判断矩阵时做了改进,使得层次分析法在高校公共选修课的选课人数爆满课程的管理中的权重设计更科学.
3 实例应用
3.1 构造层次结构模型
由于校区、资源等因素的限制使得高校公共选修课的部分课程出现选课人数爆满现象.在有限资源的情况下,对校公共选修课选课爆满课程的选课学生进行排序抽签来优化选课管理.首先,很多高校对学生选修校公共选修课有学分要求.如:江苏科技大学将校公共选修课分为两大类(人文艺术类和经管科学类),要求学生毕业必须选修10个学分校公共选修课,其中人文艺术类4个学分,经管科学类6个学分.其次,在多校区办学的背景下,校公共选修课的课程开设在校区上不能均衡,部分学生会跨校区选择容易通过的课程,经常缺课,影响教学质量.再次,校公共选修课每个学期都开设,选课学生所在年级的不同,选修某一门课程的机会不同.所以在选课过程控制中,爆满课程抽签必须要考虑学生所在年级.最后,学生是否重修该门校公共选修课,也是影响抽签结果的因素之一.构建层次结构模型如图:

3.2 构造判断矩阵
3.2.1 准则层判断矩阵的构造
在对准则层判断矩阵构造时,回避了个别领导和专家确定权重的缺点.本文在指标权重设计时,进行了改进2.由专家(含教务管理人员、教授、教师、学工管理领导和辅导员)在依据高校学籍管理规定的基础上对准则层指标的重要程度做两两比较.在两两比较时以优(+)、同等(=)和劣(-)加以表示.统计专家的比较结果,并向萨特1—9标度进行映射.对数据进行汇总分析,得出准则层判断矩阵A如表1.
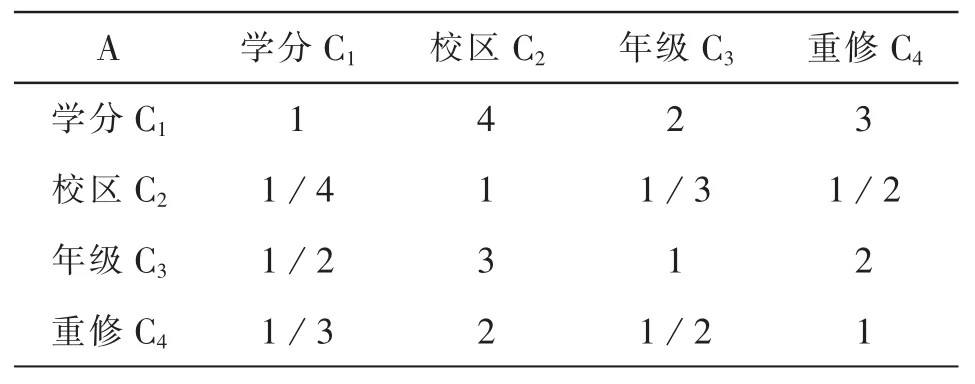
表1 准则层判断矩阵

3.2.2 方案层判断矩阵构造
对于学分这一准则判断矩阵的构造:用某一类别课程(如:经管科学类)的学校要求学分减去学生这一类别课程已修合格总学分的到的结果进行类比;对于校区的这一准则判断矩阵的构造:选课学生所在校区与课程开设校区一致设为2,否则为1;对于年级这一准则判断矩阵的构造:用学生所在年级进行比较构造;对于重修这一准则判断矩阵的构造:重修该门课程设置为2,否则为1.下面以江苏科技大学2011-2012学年第二学期校公共选修课(人文艺术类)***课程选课抽取三个学生P1、P2和P3进行构造.C1、C2、C3和 C4分别为方案层学分、校区、年级和重修的判断矩阵.

3.3 数据分析结果
由准则层的判断矩阵的一致性检验结果:W(1)=(0.466,0.096,0.277,0.161),λ=4.025,CI=0.008,CR=0.009<0.1.表明递阶层结构具有整体满意的一致性.
由方案层的判断矩阵计算到最大特征跟及权向量:W1=(0.595,0.277,0.129),λ1=3.005;W2=(0.410,0.243,0.327),λ2=3.056;W3=(0.143,0.571,0.286),λ3=3.001;W4=(0.25,0.5,0.25),λ4=3.
层 次 总 排 序 为 :W= (W1,W2,W3,W4)W(1)=(0.356,0.391,0.21).即排序结果为:P2>P1>P3.
4 小结
本文对校公共选修课选课爆满课程进行抽签排序,分析了影响制约抽签排序结果的因素,得到影响校公共选修课爆满课程抽签排序的指标体系,构建了层次结构模型.在构建准则层判断矩阵时,对公共选修课爆满课程指标引用了“序数表决,基数统计”[2]的方法,使得计算结果更科学合理.通过使用层次分析法对校公共选修课选课爆满课程进行抽签排序,优化了选课的过程管理.
〔1〕许树柏.层次分析法原理[M].天津:天津大学出版社,1988.
〔2〕袁政.政府绩效评估权重设计中AHP法之改进[J].统计研究,2008(7).
G647
A
1673-260X(2012)06-0219-02

